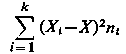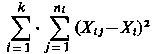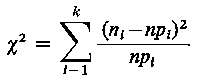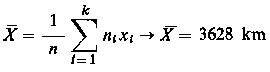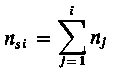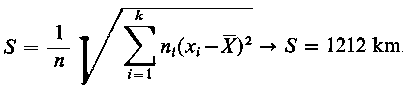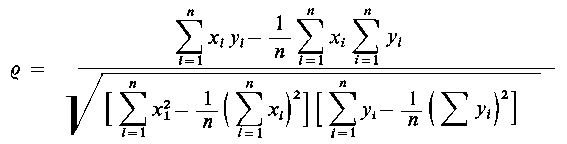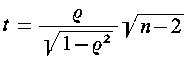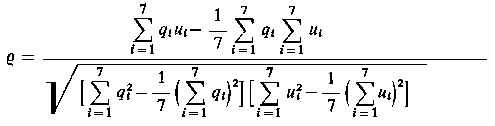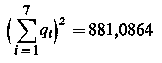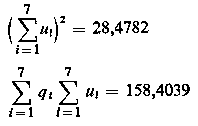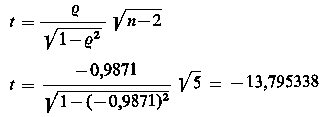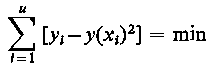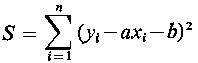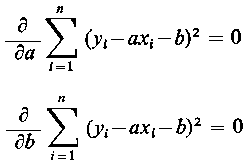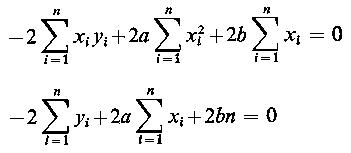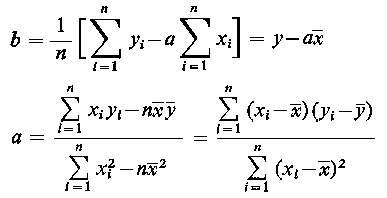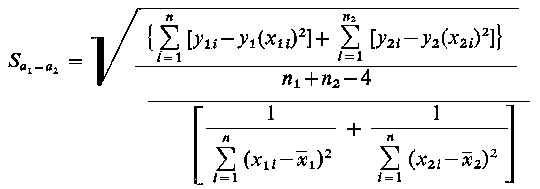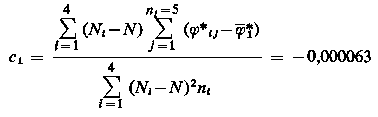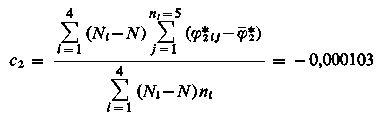| |
9.7. Planowanie trybologicznych badań eksperymentalnych i opracowanie wyników
W eksperymentalnych badaniach procesów trybologicznych oprócz czynników kontrolowanych występuje wiele czynników niekontrolowanych (przypadkowych), które również wpływają na wyniki prowadzonych badań realizowanych w warunkach określonych przede wszystkim czynnikami kontrolowanymi. Wyniki takich badań mają charakter losowy. W celu wyeliminowania wpływu czynników niekontrolowanych stosuje się odpowiednio dobrane fragmenty badań eksperymentalnych oraz metody statystycznej analizy wyników. Podstawowymi elementami układu eksperymentalnego są:
- obiekt eksperymentalny,
- jednostka eksperymentalna.
Obiektem eksperymentalnym może być każdy badany czynnik, wpływający na wynik doświadczenia. Element lub grupa elementów (np. silnik lub grupa silników) w których stosuje się obiekt eksperymentalny (np. rodzaj dodatku do oleju) nazywa się jednostką eksperymentalną. Jednostki eksperymentalne charakteryzują się tym, że uzyskuje się różne wyniki badań przy stosowaniu takiego samego obiektu. Jest to rezultatem wpływu czynników niekontrolowanych (przypadkowych) w czasie doświadczenia, jak np. niejednorodność fizyczna jednostek eksperymentalnych itp. Dlatego też badania realizuje się przez powtarzanie doświadczeń w takich samych warunkach i przy zastosowaniu takich samych obiektów eksperymentalnych.
Replikacją nazywa się powtórzenie doświadczenia dokładnie w takich samych warunkach (ze względu na wyróżnione czynniki kontrolowane), np. w określonej liczbie silników.
Powtórzeniem nazywa się czynności polegające na przeprowadzeniu identycznego doświadczenia (ze względu na kontrolowane czynniki), ale w innym miejscu (np. w innym zakładzie).
W celu wyeliminowania wpływu czynników niekontrolowanych (przypadkowych) charakteryzujących jednostki eksperymentalne dokonuje się losowego przydziału obiektów tym jednostkom. Losowy przydział obiektów jednostkom eksperymentalnym nazywa się randomizacją (random znaczy losowy).
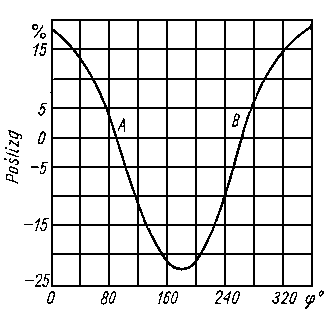
Przykład. Badany jest wpływ rodzaju dodatków do oleju na intensywność starzenia elementów silnika spalinowego samochodu. Badano dwa rodzaje olejów: olej z dodatkiem A, olej z dodatkiem B, zakładając, że oba oleje bazowe (bez dodatków) są identyczne.
Eksperyment zrealizowano w rzeczywistych warunkach eksploatacyjnych w czterech przedsiębiorstwach transportowych, wykorzystując po pięć egzemplarzy silników (pojazdów) w każdym z przedsiębiorstw dla każdego rodzaju oleju. W tak zrealizowanym eksperymencie obiektami eksperymentalnymi są rodzaje dodatków do oleju, zaś jednostkami eksperymentalnymi są egzemplarze silników. Eksperyment zrealizowano w pięciu replikacjach (po pięć silników dla każdego doświadczenia) oraz w czterech powtórzeniach (w czterech przedsiębiorstwach realizowano taki sam eksperyment).
9.7.1. Podstawowe układy eksperymentalne i ich klasyfikacja
Układy eksperymentalne charakteryzuje rozkład obiektów eksperymentalnych w zbiorze jednostek eksperymentalnych.
W zależności od celu badań i rozkładu wyróżnionych w doświadczeniu czynników, które podlegają badaniu, wyróżnia się trzy najprostsze układy eksperymentalne, oparte na randomizacji eksperymentu:
- układ kompletnej randomizacji,
- bloki kompletne zrandomizowane (bloki losowe),
- kwadrat łaciński i pochodne (hiperkwadraty).
Ze względu na rozkład kontrolowanych czynników wyróżnionych w doświadczeniu względem przyjętej klasyfikacji obiektów eksperymentalnych wyróżnia się:
- doświadczenia podlegające klasyfikacji pojedynczej,
- doświadczenia czynnikowe.
Oba rodzaje doświadczeń można zrealizować za pomocą odpowiedniego układu randomizacji.
9.7.1.1. Układ kompletnej randomizacji
Układ kompletnej randomizacji należy do najprostszych schematów planu eksperymentu. Polega ona na porównaniu wpływu c różnych obiektów eksperymentalnych na rezultaty doświadczenia przy wykorzystaniu n jednostek eksperymentalnych. Zakłada się, że jednostki eksperymentalne stanowią materiał jednorodny i są reprezentacją określonej populacji.
W ogólnym przypadku poszczególnym obiektom eksperymentalnym podporządkuje się różną liczbę jednostek eksperymentalnych, tj.: pierwszy obiekt eksperymentalny otrzymuje n1 jednostek eksperymentalnych, drugi obiekt eksperymentalny - n2 jednostek, c-ty (ostatni) obiekt eksperymentalny - nc jednostek. Zatem ogólna liczba jednostek eksperymentalnych
W wielu przypadkach nie ma potrzeby, aby podlegały wariancji liczby jednostek eksperymentalnych przydzielonych poszczególnym obiektom i wtedy każdy obiekt otrzymuje k jednostek eksperymentalnych, wobec czego
oraz
zaś poszczególne egzemplarze jednostek eksperymentalnych są przydzielane w sposób losowy poszczególnym obiektom eksperymentalnym. W tym celu wszystkim jednostkom eksperymentalnym należy przyporządkować kolejne liczby naturalne j = = l, 2, ..., n, zaś poszczególnym obiektom eksperymentalnym kolejne liczby naturalne i = l, 2, ..., c. Z tablicy liczb losowych należy wybrać dowolny ciąg liczb, ale taki, aby wystąpiła w nim każda liczba o wartości j = l, 2, ..., n co najmniej jeden raz. Z tak odnotowanego ciągu liczb należy wykreślić wszystkie liczby większe od n oraz powtórzenia liczb pozostałych (powinno więc pozostać tylko n liczb naturalnych ustawionych w przypadkowym porządku). Z tak uzyskanego ciągu liczb losowych należy wybrać: n1 kolejnych liczb określających numery jednostek eksperymentalnych przyporządkowanych obiektowi i =1, n2 kolejnych liczb określających numery jednostek eksperymentalnych przyporządkowanych obiektowi i = 2 itd. Jeżeli w doświadczeniu badana jest cecha y, to wynikami doświadczenia są pomiary tej cechy odpowiadające poszczególnym obiektom, w rezultacie czego uzyskuje się realizację zmiennych losowych y1, y2… yc, o których zakładamy, że mają rozkłady naturalne (lub zbliżone do normalnego) ze średnimi równymi odpowiednio: m1, m2, … mc o wspólnym odchyleniu standardowym.
Przykład. Badane są własności trybologiczne gumy bieżnikowej opon samochodu ciężarowego. Celem eksperymentu jest zbadanie wpływu obciążenia normalnej próbki gumowej wyciętej z bieżnika opony na wartość współczynnika tarcia podczas współpracy tej próbki z nieodkształcalną przeciwpróbką w ciągłym ruchu obrotowym. Ze względu na konieczność zbliżenia warunków badań modelowych do warunków rzeczywistych współpracy opony z nieodkształcalnym podłożem wybrano następujące wartości normalnego obciążenia próbek w N
|
1 | — | 33,1 | |
2 | — | 52,2 | |
3 | — | 69,3 | |
4 | — | 86,4
| |
W celu przeprowadzenia eksperymentu ułożono po trzy replikacje doświadczeń względem każdego obiektu (obciążenia); w związku z tyra wykonano
n = 4.3 = 12 próbek
Ze względu na to, że w materiale opony mogą wystąpić nieznane niejednorodności, podział próbek stanowiących jednostki eksperymentalne wykonano w układzie kompletnej randomizacji przy zachowaniu jednakowej liczby replikacji dla poszczególnych wartości obciążeń normalnych. W tym celu ponumerowano poszczególne próbki gumy bieżnika numerami j = 1, 2, ..., 12, zaś z tablic liczb losowych odczytano następujący ciąg liczb, w których liczby j = l, 2, ..., 12 występują co najmniej raz
{84, 12, 06, 49, 53, 10, 12, 01, 06, 15, 04, 59, 93, 47, 02, 19, 33, 48, 57, 11, 16, 24,
05, 46, 68, 73, 03, 18, 88, 09, 05, 61, 64, 07, 20, 07, 12, 08}.
Ze zbioru tego należy wykreślić wszystkie liczby większe od 12 oraz te, które są powtórzeniami pozostałych liczb od l do 12; zatem uzyskano następujący ciąg liczb:
12, 06,10, 01, 04, 02, 11, 05, 03, 09, 07, 08.
Tak uzyskany ciąg liczb podzielono na cztery zbiory, przyporządkowując w ten sposób numery próbek (jednostek eksperymentalnych) poszczególnym obiektom (obciążeniom normalnym). Uzyskano zatem:
-próbki o numerach: {12, 06, 10} będą badane pod obciążeniem nr l równym 33,1 N,
- próbki o numerach: {01, 04, 02} będą badane pod obciążeniem nr 2 równym 52,2 N,
- próbki o numerach: {11, 05, 03} będą badane pod obciążeniem nr 3 równym 69,3 N,
- próbki o numerach: {09, 07, 08} będą badane pod obciążeniem nr 4 równym 86,4 N.
Tak uzyskany plan eksperymentu można przedstawić w postaci macierzy bądź tablicy liczbowej o wartościach jednostkowych. Przyjmując numery wierszy odpowiadające numerom obiektów eksperymentalnych (i = l, 2, 3, 4) oraz numery kolumn odpowiadające numerom jednostek eksperymentalnych mamy następujący plan eksperymentu
|
p = |
 |
0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 |
 | |
l | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | |
0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | |
| |
gdzie: wartość 1 znajdująca się w wierszu i kolumny j oznacza, że jednostka eksperymentalna, jaką jest próbka o numerze j, będzie badana względem obiektu - pod obciążeniem normalnym - o numerze i .
9.7.1.2. Bloki kompletnie zrandomizowane
W wielu przypadkach rzeczywista sytuacja badawcza uwarunkowana dysponowanym materiałem doświadczalnym powoduje, że nie można z góry w sposób arbitralny założyć, iż wszystkie jednostki eksperymentalne tworzą próbkę jednorodną. Jeżeli posiadany materiał doświadczalny można pogrupować wg znanego (lub spodziewanego) czynnika w taki sposób, że jednostki eksperymentalne zaliczone do danej grupy tworzą zbiór jednorodny, to plan eksperymentu powinien zapewnić wyeliminowanie z błędu eksperymentalnego zmienność wyników pochodzącą od czynnika grupującego. Jedną z najprostszych metod zapewniających osiągnięcie tego celu jest metoda bloków kompletnie zrandomizowanych. Założenia metody są następujące:
1. Z n jednostek eksperymentalnych stanowiących materiał doświadczalny należy stworzyć równoliczne grupy, zwane blokami, w taki sposób, aby jednostki te możliwie mało różniły się między sobą wewnątrz grup; dopuszczalne są różnice między grupami.
2. Liczba jednostek w bloku powinna być równa liczbie obiektów eksperymentalnych c.
3. Każdej z c jednostek eksperymentalnych w danym bloku należy przyporządkować w sposób losowy jeden z c obiektów eksperymentalnych. Randomizację tę należy wykonać niezależnie wewnątrz każdego bloku. W rezultacie tego uzyskuje się k bloków stanowiących replikacje, przy czym liczba replikacji jest dowolna i uwarunkowana najczęściej możliwościami technicznymi realizacji badań. Otrzymane tak rezultaty eksperymentu podlegają podwójnej klasyfikacji:
- ze względu na bloki (czynnik grupowy),
- ze względu na obiekty.
Każda z jednostek eksperymentalnych stanowi element tej klasyfikacji : należy do jednego z k bloków i c obiektów eksperymentalnych. Randomizację jednostek eksperymentalnych wewnątrz bloków należy przeprowadzić w sposób identyczny jak dla układów kompletnej randomizacji z tą tylko różnicą, że w każdym z bloków każdy obiekt otrzymuje tylko jedną jednostkę eksperymentalną (bez replikacji).
P r z y k ł a d. Rozpatrzmy problem sformułowany w przykładzie w pkcie 9.7.2 z tą różnicą, że dla uogólnienia wyników doświadczeń próbki gumy bieżnika opon wykonano z trzech egzemplarzy opon. Każda pochodzi z innej partii. Można więc w tym przypadku spodziewać się skażenia wyników badań zmiennością pochodzącą od czynnika grupującego, jakim jest egzemplarz opony. Zatem, w celu wyeliminowania wpływu egzemplarza opony na błąd eksperymentu, przeprowadzono eksperyment metodą bloków kompletnie zrandomizowanych. Utworzono trzy bloki odpowiadające trzem egzemplarzom opon. Z tego każdy blok składa się z czterech próbek gum bieżnikowych wyciętych z odpowiadających im egzemplarzy opon. Dokonując losowego podziału obiektów między poszczególne jednostki eksperymentalne w blokach uzyskano następujący
Tablica 9.6. Przykład planu eksperymentu|
Bloki | 1 | 2 | 3 | |
Obiekty (numery wartości obciążeń normalnych) |
2 | 3 | 4 | |
3 | 1 | 3 | |
1 | 4 | 2 | |
4 | 2 | 1
| |
plan eksperymentu przedstawiony w tabl. 9.6. Dowolny element tej tablicy Xij o wartości liczbowej równej a oznacza, że jednostka eksperymentalna o numerze i (próbka bieżnika opony) należąca do bloku j (wycięta z opony o numerze j) jest przyporządkowana obiektowi o numerze a (odpowiedniej wartości obciążenia normalnego o numerze a).
9.7.1.3. Kwadrat łaciński
Jeżeli zbiór jednostek eksperymentalnych stanowiących materiał doświadczalny podlega klasyfikacji ze względu na dwa czynniki grupujące, wtedy plan eksperymentu należy przeprowadzić metodą kwadratów łacińskich.
kwadrat łaciński. Przez rozumie się uszeregowanie n = c² jednostek eksperymentalnych, które podlegają podwójnej klasyfikacji: ze względu na c bloków jednego rodzaju zwanych wierszami i ze względu na c bloków drugiego rodzaju zwanych kolumnami. Kwadrat łaciński ma własność, że każdy z c obiektów eksperymentalnych występuje dokładnie c razy, a w tym po jednym razie w każdym wierszu i po jednym razie w każdej kolumnie. Przyporządkowanie c obiektów c-krotnie replikowanych realizuje się na zasadzie randomizacji.
Określenie kwadrat łaciński wiąże się z tym, że poszczególne obiekty eksperymentalne są oznaczone literami alfabetu łacińskiego: A, B, C, ..., itd. Cechą kwadratu łacińskiego jest to, że na porównanie obiektów nie mają wpływu przeciętne różnice między wierszami a kolumnami. Cecha ta nosi nazwę ortogonalności. Randomizację kwadratu łacińskiego można wykonać randomizując kwadrat łaciński zredukowany, w którym w pierwszym wierszu i w pierwszej kolumnie litery są uporządkowane alfabetycznie. Przykładem kwadratu łacińskiego zredukowanego rzędu 4 x 4 jest kwadrat:
W tym przypadku można zastosować jeszcze dwa warianty kwadratów zredukowanych rzędu 4x4.
Przy planowaniu doświadczenia metodą kwadratów łacińskich należy zrealizować następujący ciąg czynności:
1) wybrać dowolny kwadrat łaciński zredukowany rzędu c x c (c - liczba obiektów),
2) dokonać losowego przestawienia wszystkich wierszy poza pierwszy korzystając z ciągu liczb losowych,
3) dokonać losowego przestawienia wszystkich kolumn korzystając z ciągu liczb losowych,
4) dokonać losowego przyporządkowania obiektów eksperymentalnych poszczególnym literom A, B, C, ... za pomocą ciągu liczb losowych, przyjmując że poszczególnym literom odpowiadają kolejne obiekty eksperymentalne.
Przykład. Planowane jest doświadczenie dla czterech obiektów eksperymentalnych metodą kwadratu łacińskiego rzędu 4 x 4. W tym celu wybrano kwadrat łaciński zredukowany:
Losowego p r z e s t a w i e n i a w i e r s z y dokonano na podstawie ciągu liczb losowych {3, 4, 2}, co oznacza, że:
- pierwszy wiersz zostaje niezmieniony,
- drugi wiersz należy przestawić na pozycję wiersza trzeciego,
- trzeci wiersz należy przestawić na pozycję wiersza czwartego,
- czwarty wiersz należy przestawić na pozycję wiersza drugiego,
zatem uzyskano kwadrat:
Losowego przestawienia kolumn dokonano na podstawie ciągu liczb losowych {3, l, 4, 2}, zatem uzyskano:
Losowe przyporządkowanie obiektów literom A, B, C, D wykonano za pomocą ciągu liczb losowych {4, 2, l, 3}, tzn.
A → 4
B → 2
C → l
D → 3
uzyskując kwadrat:
Operację tę wykonano w następujący sposób: litery A, B, C, D ponumerowano liczbami l, 2, 3, 4. Następnie przyporządkowanie literze A liczby 4 oznacza, że litera A powinna być przestawiona na miejsce litery oznaczonej numerem 4 czyli D. Podobnie przyporządkowanie literze D liczby 2 oznacza, że litera B pozostaje bez zmiany (bo jest z numerem 2). Przyporządkowanie literze C liczby l oznacza, że litera C powinna być przestawiona na miejsce litery A itd.
Przykład. Badane są własności trybologiczne tworzyw sztucznych przez pomiar współczynnika tarcia oraz odporności na zużycie dla sześciu tworzyw z różnymi wypełniaczami metalowymi przy różnych wartościach temperatury oraz nacisków jednostkowych. W eksperymencie tym występują więc trzy źródła zmienności:
- temperatura (efekt wierszy),
- naciski jednostkowe (efekt kolumnowy),
- rodzaj tworzywa (efekt obiektowy).
W celu zbadania wpływu wypełniaczy metalowych na własności trybologiczne tworzywa w warunkach różnych nacisków jednostkowych oraz temperatury, zaplanowano eksperyment metodą kwadratów łacińskich. W tym celu rozlosowano rodzaje tworzyw między litery alfabetu łacińskiego uzyskując następujące przyporządkowanie:
|
Symbol tworzywa | Litera | |
P-M15 | A | |
P | B | |
P-A10 | C | |
P - M 20 | D | |
P-M10 | E | |
P-A15 | F
| |
przy czym poszczególnym symbolom tworzyw odpowiada tworzywo o określonej zawartości wypełniaczy metalowych, jakimi są: proszek mosiądzu, proszek aluminium, drut cynkowy.
Do przeprowadzenia eksperymentu wg kwadratu 6x6 zastosowano temperatury:
{100, 180, 260, 340, 420, 500} °C
odpowiadające kolejnym numerom wierszy l-6, oraz naciski jednostkowe o wartościach:
0,4; 0,6; 0,8; 1,0; 1,2; 1,4; MPa
odpowiadające numerom kolumn 1-6.
Przyjmując kwadrat zredukowany 6x6 postaci:
|
A | B | C | D | E | F | |
B | F | D | C | A | E | |
C | D | E | F | B | A | |
D | A | F | E | C | B | |
E | C | A | B | F | D | |
F | E | B | A | D | C
|
dokonano randomizacji uzyskując kwadrat łaciński o postaci:
|
C | B | F | E | D | A | |
F | C | D | B | A | E | |
D | E | C | A | F | B | |
A | D | E | F | B | C | |
E | A | B | D | C | F | |
B | F | A | C | E | D
|
Należy przy tym pamiętać, że poszczególnym kolumnom odpowiadają kolejne wartości nacisków jednostkowych, zaś wierszom - wartości temperatury. Interpretacja dowolnego elementu yij tego planu oznacza, że jednostka eksperymentalna, której odpowiada obiekt określony literom stojącym w i wierszu oraz w j kolumnie będzie badana w temperaturze o numerze i w warunkach nacisków jednostkowych j. I tak element y23 = D oznacza, że tworzywo P-M20 odpowiadające literze D w temperaturze 180°C (i = 2) będzie badane przy naciskach jednostkowych 0,8 MPa (j = 3) itd.
9.7.2. Doświadczenia czynnikowe
W opisanym eksperymencie rolę obiektu spełniały wypełniacze metalowe tworzywa przy zastosowaniu jednakowego tworzywa bazowego. Jeżeli konieczne jest jednoczesne uwzględnienie dwóch czynników zmiennych, np. rodzaju żywicy oraz rodzaju wypełniacza, wtedy przedstawiony kwadrat łaciński nie wystarczy do zrealizowania eksperymentu. W takiej sytuacji należy założyć doświadczenie, w którym obiektami eksperymentalnymi są wszystkie możliwe kombinacje pomiarów wyróżnionych czynników. Po określeniu w ten sposób obiektów eksperymentalnych dalsze planowanie realizuje się wg jednego z przedstawionych układów eksperymentalnych. Najprostszym doświadczeniem czynnikowym jest doświadczenie typu 2x2, tzn. takie, w którym występują dwa czynniki na dwóch poziomach. Poziomy te można oznaczyć symbolami 0 i l. Zestawienie poziomów obu czynników daje cztery kombinacje, które można oznaczyć symbolami:
00 lub a0b0 lub A
10 lub a1b0 lub B
01 lub a0b1 lub C
11 lub a1b1 lub D
Można założyć, że doświadczenie to, przy danej liczbie replikacji zależnie od sytuacji badawczej - jest realizowane jednym z trzech układów:
1) w układzie kompletnej randomizacji,
2) w układzie bloków kompletnie zrandomizowanych,
3) w układzie kwadratu łacińskiego.
Sposób postępowania jest identyczny jak w przypadkach już opisanych.
9.7.3. Estymacja wartości średniej dla populacji generalnej na podstawie wyników badań próby
Średnia wartość badanej cechy mierzonej jest najczęściej szacowanym parametrem populacji generalnej. Jakkolwiek większość eksperymentatorów usiłuje z reguły wykorzystywać jedynie wynik estymacji punktowej - średniej, to jednak dla zachowania poprawności wnioskowania bardziej celowa jest metoda estymacji przedziałowej. Metoda estymacji przedziałowej umożliwia określenie pewnego przedziału wartości liczbowych, który z dużym (z góry przyjętym) prawdopodobieństwem obejmuje prawdziwą wartość średnią. Najlepszym estymatorem dla średniej m populacji generalnej jest średnia arytmetyczna X z próby. Jest to estymator zgodny, nieobciążony, efektywny i dostateczny. Oszacowanie wartości średniej z próby uzyskuje się na podstawie prostego wyrażenia
|
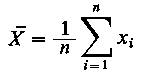
| (9.66)
|
gdzie xi - rezultat i replikacji.
W praktyce najczęściej jest stosowany następujący model do wyznaczania przedziałów ufności dla średniej: populacja generalna na rozkład N(m, σ), przy czym nieznana jest wartość średnia m populacji i odchylenie standardowe σ w populacji. Z populacji tej wylosowano małą próbkę o liczności a elementów (jednostek eksperymentalnych). Po uzyskaniu wyników doświadczenia przedziału ufności dla średniej m populacji można wyznaczyć z zależności
|
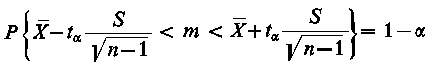
| (9.67)
|
gdzie X - średnia arytmetyczna obliczona z wyników próby przy czym odchylenie standardowe z próby oblicza się wg wzoru
|
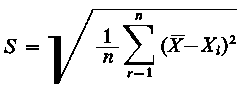
| (9.68)
|
gdzie: X - średnia arytmetyczna obliczona z wyników próby, 1-α - założone z góry prawdopodobieństwo zwane poziomem (współczynnikiem) ufności, tα - wartość rozkładu t - Studenta odczytana z tablic tego rozkładu dla n - 1 stopni swobody przy spełnieniu relacji
|
P ( -tα < t < 1 - tα ) = 1 - α
| (9.69)
|
Założona wartość tα, na ogół bliska jedności, określa prawdopodobieństwo, z jakim rzeczywista wartość średnia m populacji znajduje się w obliczonym przedziale ufności.
Przykład. Podczas badań własności ciernych gum bieżnikowych w różnych warunkach obciążenia normalnego próbki bieżnika okazuje się, że wartości średnich nacisków jednostkowych w obszarze tarcia nie są określone. I tak, dla próbek bieżnika opony STOMIL, dla kilku obciążeń normalnych próbek uzyskano wartości średnich nacisków jednostkowych w obszarze tarcia wyszczególnione w tabl. 9.7.
Tablica 9.7. Wyniki pomiarów średnich nacisków jednostkowych dla różnych obliczeń próbek bieżnika opony|
Numer obciążenia | Obciążenie | Numer próbki | |
1 | 2 | 3 | 4 | 5 | 6 | |
1 | 3,31 | 2,583 | 2,468 | 2,432 | 2,399 | 2,359 | 2,324 | |
2 | 5,22 | 3,401 | 3,357 | 3,293 | 3,271 | 3,240 | 3,222 | |
3 | 6,93 | 3,920 | 3,812 | 3,772 | 3,702 | 3,657 | 3,619 | |
4 | 8,64 | 4,623 | 4,509 | 4,486 | 4,499 | 4,424 | 4,361 | |
5 | 10,35 | 5,078 | 4,841 | 4,803 | 4,770 | 4,715 | 4,666 | |
6 | 12,06 | 5,494 | 5,348 | 5,320 | 5,257 | 5,230 | 5,158 | |
7 | 13,77 | 5,897 | 5,692 | 5,607 | 5,535 | 5,508 | 5,497
| |
Zatem, ze względu na znaczny wpływ składnika losowego na wyniki pomiarów nacisków jednostkowych, do ich oszacowania zbudowano przedziały ufności. W tym celu policzono wartości średnie q
oraz wariancje
|
|
|
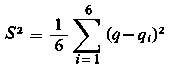
Zakładając poziom ufności 1-α = 0,95, tzn. α = 0,05, oraz przyjmując liczbę stopni swobody równą 5, z tablic rozkładu t-Studenta znajduje się wartość tα = t0,05 = 2,571. Stąd łatwo wyznaczyć granice przedziału ufności oznaczone umownie symbolami:
|
|
|
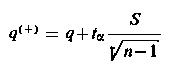
- granica prawostronna
|
|
|
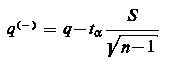
- granica lewostronna
Wyniki obliczeń podano w tabl. 9.8.
Tablica 9.8. Wyniki obliczeń przedziałów ufności w badaniach tarcia gum bieżnikowych|
Numer obciążenia | q | S² | t | q(-) | q(+) | |
1 | 2,428 | 0,008 | 2,571 | 2,331 | 2,524 | |
2 | 3,297 | 0,005 | 2,571 | 3,225 | 3,370 | |
3 | 3,747 | 0,012 | 2,571 | 3,631 | 3,863 | |
4 | 4,475 | 0,008 | 2,571 | 4,382 | 4,569 | |
5 | 4,812 | 0,021 | 2,571 | 4,661 | 4,964 | |
6 | 5,301 | 0,013 | 2,571 | 5,179 | 5,423 | |
7 | 5,623 | 0,023 | 2,571 | 5,462 | 5,783
| |
Szerokość przedziału ufności nie przekracza na ogół 10% wartości średniej, co świadczy o powtarzalności wyników badań, a więc o małym ryzyku przy uogólnieniu wniosków dotyczących populacji generalnej. Podczas szacowania wartości średniej badanej cechy trybologicznej dla populacji generalnej ważne jest zaplanowanie niezbędnej liczby pomiarów (replikacji). W większości przypadków przy rozpoczynaniu badania jest nieznana zarówno wartość średnia, jak i wariancja badanej cechy. Zatem w celu określenia niezbędnej liczby powtórzeń doświadczenia, należy przeprowadzić badania wstępne na małej próbce o liczności n0, uzyskując oszacowanie wartości średniej X oraz estymatora wariancji Ŝ²
|
|
|
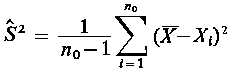
Przyjmując, że oszacowanie wartości średniej dla badanej cechy powinno być wykonane z błędem nie przekraczającym z góry zadanej wartości d z poziomem ufności 1-α, niezbędną liczbę powtórzeń doświadczenia można obliczyć ze wzoru
gdzie tα - wartość rozkładu (t-Studenta dla n0 - l stopni swobody i wartości 1-α poziomu ufności.
Gdyby się okazało, że obliczona wartość n jest nie większa od wartości n0, wówczas należy uznać, że zrealizowane badania wstępne są wystarczające. Należy tu dodać, że obliczoną wartość n należy zawsze zaokrąglać do najbliższej, większej od niej liczby całkowitej, gdyż tylko liczba całkowita może być liczbą doświadczeń.
Przykład. Podczas badań własności ciernych gum bieżnikowych wykonano sześć próbek i zbadano rozrzut wartości współczynnika tarcia wokół wartości średniej. Po obliczeniu wartości średniej i wariancji z próby uzyskano wartość Ŝ²= 0,0004.
Jeżeli wymagana dokładność oszacowania wartości średniej współczynnika tarcia gumy bieżnikowej opon jest rzędu 0,01, to przyjmując poziom ufności 1-α = 0,95, niezbędna liczba doświadczeń wynosi
|
n = |
tα²Ŝ²
d² |
= |
2,571² • 0,0004
0,01² |
≈ 27
|
|
Ponieważ wykonano już sześć doświadczeń, zatem należy jeszcze wykonać dwadzieścia jeden, aby uzyskać wymaganą dokładność oszacowania wartości średniej współczynnika tarcia.
9.7.4. Wnioskowanie statystyczne na podstawie parametrycznych testów istotności
Wyniki badań opracowane najczęściej w postaci wartości średnich badanej cechy oraz przedziałów ufności nie pozwalają wyciągnąć daleko idących wniosków. Wynika to stąd, że wartości średnie z badań podlegają także losowym fluktuacjom. Jeżeli zbadano tę samą cechę X dwu populacji (lub dwu różnych obiektów eksperymentalnych) - uzyskując różne wartości średnie X1 oraz X2, to na podstawie porównania samych wartości średnich X1 i X2 nie można powiedzieć, czy ewentualne różnice tych wartości są istotne. Pierwszym etapem analizy wyników badań eksperymentalnych jest zbadanie, czy czynniki uwzględnione w planie eksperymentu mają istotny wpływ na uzyskane wyniki badań. W tym celu należy postawić szereg hipotez statystycznych, które weryfikuje się za pomocą znanych, parametrycznych testów istotności. Sposób weryfikacji hipotez zależy od planu eksperymentu, w związku z tym metoda postępowania zostanie przedstawiona dla przypadku najprostszego, gdy badana próba podlega klasyfikacji pojedynczej (co odpowiada układom kompletnej randomizacji). Pozwoli to w wystarczającym stopniu zrozumieć sposób i sens postępowania przy weryfikacji hipotez statystycznych.
Spośród wielu testów parametrycznych do badania wartości średnich najczęściej są stosowane:
- test dla dwóch średnich,
- test analizy wariancji dla wielu średnich.
9.7.4.1. Test dla dwóch średnich
Test ten służy do porównania wartości średnich dwu populacji na podstawie wyników prób. Zakłada się, że badane populacje mają rozkłady normalne N(m1, σ1) oraz N(m2, σ2), przy czym odchylenia standardowe tych populacji są nieznane, ale jednakowe, tzn. σ1 = σ2. Na podstawie wyników dwu małych prób odpowiednio o licznościach n1 i m2, wylosowanych niezależnie z tych populacji należy zweryfikować hipotezę H0: n1 = m2 wobec hipotezy alternatywnej H1: m1 ≠ m2 . Z wyników obu prób należy policzyć wartości średnie X1 i X2, oraz wariancje S1² i S2², a następnie wartość rozkładu t-Studenta
|
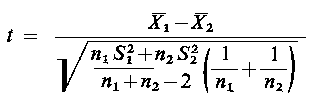
| (9.70)
|
Statystyka ta ma przy założeniu prawdziwości hipotezy H0 rozkład t-Studenta o n1+n2-2 stopniach swobody. Odczytując z tablic rozkładu t-Studenta dla n1+n2-2 stopni swobody oraz dla założonego z góry poziomu istotności α wartość krytyczną tα, należy porównać ją z obliczoną wartością t.
Jeżeli:
| t | ≥ tα
to weryfikowaną hipotezę H0 należy odrzucić, w przeciwnym przypadku nie ma podstaw do odrzucenia hipotezy H0.
W przypadku, gdy liczności prób są duże — rzędu kilkudziesięciu — wówczas do weryfikacji testu należy przeliczyć statystykę U
|
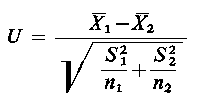
| (9.71)
|
która przy założeniu prawdziwości hipotezy H0 ma rozkład normalny N(0, 1). Zatem z tablicy rozkładu normalnego N(0, 1) należy dla przyjętego z góry poziomu istotności α wyznaczyć taką wartość krytyczną Uα, która spełnia nierówność
|
P { | U | ≥ Ua } = α
| (9.72)
|
Porównując odczytaną wartość Uα z wartością U, hipotezę H0 należy odrzucić, jeżeli jest spełniona nierówność w przeciwnym przypadku nie ma podstaw do odrzucenia hipotezy H0.
Przykład. Badane są własności cierne gum bieżnikowych dwóch rodzajów opon: opona STOMIL i opona PIRELLI. W rezultacie przeprowadzonych badań uzyskano następujące wartości współczynnika tarcia µ dla obciążenia normalnego próbek wynoszącego 33,1 N (tabl. 9.9). Porównując własności cierne obu opon postawiono hipotezę H0: µ1 = µ2 wobec hipotezy alternatywnej H1: µ1 ≠ µ2.
Tablica 9.9. Wyniki pomiarów współczynnika tarcia próbek gum bieżnikowych przy obciążeniu normalnym|
Rodzaj opony | Numer próbki | |
1 | 2 | 3 | 4 | 5 | 6 | | |
STOMIL | 0,856 | 0,852 | 0,861 | 0,861 | 0,861 | 0,867 | 0,8612 | |
PIRELLI | 0,854 | 0,880 | 0,905 | 0,904 | 0,894 | 0,873 | 0,8850
| |
Jak wynika z zestawionych wyników wyciągania wniosków tylko na podstawie porównania wartości średnich µ1, µ2 jest ryzykowne, ponieważ wartości uzyskane w poszczególnych pomiarach są zbliżone. Po obliczeniu wartości średnich µ1, µ2 oraz wariancji S1², S2² i podstawieniu do wyrażenia na rozkład t Studenta otrzymamy wartość t = 2,845. Liczba stopni swobody wynosi w tym wypadku 6+6-2 = 10. Zatem dla α = 0,05, wartość tα wynosi t0,05 = 2,228. Ponieważ 2,845 jest większe od 2,228 zatem hipotezę H0 należy odrzucić. Oznacza to, że opony STOMIL i PIRELLI istotnie różnią się własnościami ciernymi (współczynnikiem tarcia) gum bieżnikowych. Oczywiście, wniosek ten jest słuszny dla zbadanego obciążenia normalnego, przy czym ryzyko poprawności wniosku jest rzędu 0,05.
9.7.4.2. Test analizy wariancji dla wielu średnich
Test ten stosuje się przy porównywaniu wielu średnich pochodzących od różnych obiektów lub populacji. Przeprowadza się go wg określonego schematu ujętego w postaci tzw. tablicy analizy wariancji. Danych jest k populacji o rozkładzie normalnym N(mi, σi) (i = l, 2, …, k) lub o rozkładzie zbliżonym do normalnego. Zakłada się, że wariancje wszystkich k populacji są różne. Z każdej populacji wylosowano niezależnie próby o liczności n, elementów, uzyskując wyniki xij (i = 1,2, …, k, j = l, 2, …,ni) badanej cechy. Na podstawie wyników badań zweryfikować należy hipotezę H0: m1 = m2 = … = mk wobec hipotezy alternatywnej H1: nie wszystkie badane średnie populacji są równe. W celu zweryfikowania hipotezy H0 należy policzyć wartości średnie Xi dla i = 1,2, ..., k,
oraz ogólną średnią X
gdzie  .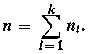
Z kolei należy obliczyć odpowiednie sumy kwadratów i wariancje, wypełniając nimi tabliczkę analizy wariancji (tabl. 9.10).
Tablica 9.10. Analiza wariancji|
Źródło zmienności | Suma kwadratów
SS | Stopnie swobody | Wariancje
| Test
F | |
Między populacjami (grupami zmienności) | 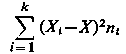 | k = 1 | S1² | | |
Wewnątrz grup | 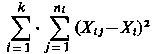 | n - k | S2²
| |
Obliczoną statystykę F należy porównać z wartością krytyczną Fα odczytaną z tablic rozkładu F Snedecora dla ustalonego z góry poziomu istotności α i dla odpowiedniej liczby r1 = k - 1, r2 = n - k stopni swobody.
Jeżeli F ≥ Fα, to hipotezę H0 o równości średnich w badanych populacjach należy odrzucić, w przeciwnym przypadku nie ma podstaw do odrzucenia hipotezy H0.
Jeżeli F < 1, wówczas bez porównywania z wartością F nie ma podstaw do odrzucenia hipotezy H0. Odrzucenie hipotezy H0 oznacza, że wpływ dokonanego podziału na badane próby (populacje) jest istotny, w przeciwnym zaś przypadku można uważać wszystkie badane próby za równoważne pod względem otrzymanych wartości badanej cechy.
Przykład. Badany jest wpływ temperatury nakładek hamulca samochodów na wartość współczynnika tarcia (nakładki wykonane dla celów doświadczalnych). Wyniki badań modelowych współczynnika tarcia przedstawiono w tabl. 9.11, wpisując wartości Xij = kij•100. Analizę wariancji dla zbadania istotności wpływu temperatury podano w tabl. 9.12.
Tablica 9.11. Wyniki badań modelowych współczynnika tarcia nakładek hamulcowych
Temperatura
°C | Powtórzenie | |
1 | 2 | 3 | 4 | 5 | 6 | |
100 | 35,8 | 32,2 | 32,3 | 32,0 | 31,4 | 34,5 | |
200 | 37,7 | 34,1 | 35,9 | 33,2 | 32,8 | 36,3 | |
300 | 39,8 | 35,2 | 35,1 | 34,9 | 33,8 | 37,2 | |
400 | 35,1 | 31,3 | 31,1 | 32,0 | 30,6 | 32,9
| |
Tablica 9.12. Analiza wariancji|
Źródło zmienności | Suma kwadratów
SS | Stopnie swobody | Wariancje
| Test
F | |
Między populacjami (grupami zmienności) | 60 | k - 1 = 3 | 20 | 5,63 | |
Wewnątrz grup | 71 | n - k = 20 | 3,55
| |
Ponieważ wartości Fα dla a = 0,05 wynosi F0,05 = 3,10, zatem F > Fα. Stąd wynika wniosek, że wpływ temperatury na wartość współczynnika tarcia nakładek hamulcowych z tego tworzywa jest istotny.
Ważnym etapem opracowania wyników badań jest analiza wyników w zakresie rozkładu badanej cechy populacji generalnej. Do weryfikacji rozkładu badanej cechy stosuje się tzw. testy zgodności, spośród których najczęściej są stosowane:
- test zgodności χ²,
- test zgodności λ Kołmogorowa.
9.7.5. Test zgodności χ²
Tekst zgodności χ² pozwala zweryfikować hipotezę, że populacja generalna ma określony typ rozkładu Ω o znanej funkcji dystrybuanty. Rezultaty obserwacji badanej cechy X populacji generalnej należy podzielić na k rozłącznych klas o licznościach ni w każdej klasie (i = 1,2, ..., k), uzyskując przez to rozkład empiryczny (tabl. 9.13).
Tablica 9.13. Podział na rozłączne klasy wyników obserwacji badanej cieczy|
xi | ni | |
x1 | n1 | |
x2 | n2 | |
. | . | |
. | . | |
. | . | |
xk | nk
| |
Na podstawie tak uporządkowanych wyników badań należy sprawdzić hipotezę H0, że populacja generalna ma rozkład typu Ω, tzn. H0: F(x)Ω, gdzie F(x) jest dystrybuantą rozkładu populacji.
Zakładając hipotetyczny rozkład o dystrybuancie F(x) należy oszacować parametry tego rozkładu na podstawie uzyskanych wyników badań, a następnie obliczyć dla każdej z k klas wartości badanej cechy X - prawdopodobieństwa pi, że zmienna losowano rozkładzie Ω przyjmuje wartości należące do klasy o numerze i. Mnożąc wartości pi przez liczność całej próby n otrzymuje się liczności teoretyczne n pi, które powinny wystąpić w klasie i, jeżeli populacja ma rozkład typu Ω, tzn. jeżeli hipoteza H0 jest prawdziwa. Porównując liczności empiryczne ni oraz hipotetyczne n pi, należy wyznaczyć wartość statystyki χ²
|
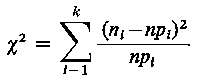
| (9.73)
|
która przy założeniu prawidłowości hipotezy H0 ma rozkład asymptotyczny χ² o k - r - l stopniach swobody, gdy k parametrów rozkładu Ω szacowano z próby.
Znając z tablicy rozkładu wartość χ² dla k - r - l stopni swobody i założonego poziomu istotności a wartość graniczną χ², należy sprawdzić czy zachodzi relacja
χ²≥ χ²α
Jeśli występuje taka zależność, to hipotezę H0, że populacja generalna ma rozkład typu Ω, należy odrzucić. W przeciwnym przypadku nie ma podstaw do odrzucenia hipotezy H0. Test zgodności χ² jest tak zbudowany, że im bliższa zeru wartość statystyki χ², tym hipoteza H0 jest bardziej wiarygodna.
Przykład. Badany jest rozkład intensywności zużycia elementów układu bieżnego pojazdów gąsienicowych. W tym celu obserwowano m.in. zmiany średnicy przegubów w ogniwach taśmy gąsienicy, uzyskując następujące wartości przebiegów w km ogniw gąsienic do chwili uzyskania powiększenia średnicy przegubu o wartości 3,5 nm (tabl. 9.14).
Tablica 9.14. Wartości przebiegów w kilometrach przegubowych ogniw gąsienicowych|
Przebiegi, km | Liczba ogniw | |
1 200÷2 000 | 5 | |
2 000÷2 800 | 6 | |
2 800÷3 600 | 11 | |
3 600÷4 400 | 8 | |
4 400÷5 200 | 8 | |
5 200÷6 000 | 5
| |
Łącznie przeprowadzono obserwację 43 ogniw gąsienicy. Średni przebieg ogniw do uzyskania ww. wartości zużycia wynosi
gdzie xi - środkowa wartość przedziału o numerze i
9.7.6. Test zgodności l Kołmogorowa
Drugim podstawowym testem zgodności jest nieco mniej pracochłonny test zgodności Kołmogorowa oparty na statystyce l. Test ten jednak stosuje się tylko do weryfikacji rozkładów zmiennych losowych ciągłych.
Na podstawie wyników badań empirycznych weryfikuje się hipotezę H0: że dystrybuanta F( x ) rozkładu ciągłego badanej cechy populacji generalnej ma postać F0( x ), tzn. F( x ) = F0( x ), gdzie F0( x ) jest konkretną, hipotetyczną i ciągłą dystrybuantą.
W celu zweryfikowania hipotezy H0 należy wyniki prób uporządkować grupując je w stosunkowo wąskie przedziały o prawych końcach xi i odpowiadających im licznościach ni, znajdując wartości empirycznej dystrybuanty Fn( x ) z zależności
przy czym nsi oznacza skumulowana od początku aż do xi liczebność, tzn.
|
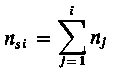
| (9.75)
|
Następnie z hipotetycznego rozkładu znajduje się wartości teoretyczne dystrybuanty F( x ) oraz największą różnicę między wartościami dystrybuanty teoretycznej i empirycznej
|
D = sup [ Fn ( xi) - F ( xi) ]
| (9.76)
|
oraz wartość statystyki λ
zaś odchylenie standardowe
|
|
|
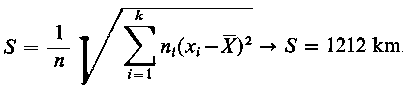
Na podstawie rozkładu empirycznego należy sprawdzić hipotezę H0: że rozkład przebiegów ogniw gąsienic do chwili uzyskania określonej wartości zużycia przegubu jest rozkładem normalnym. Obliczenia można wykonać posługując się tabl. 9.15.
Dla poziomu istotności α = 0,05 oraz stopni swobody 6 - 2 - l = 3 wartość graniczna χ0,05 wynosi 0,49. Ponieważ
χ < χ0,05
Tablica 9.15. Weryfikacja charakteru rozkładu danych empirycznych do badań zużycia przegubów ogniw gąsienicowych
Końce
przedziału
xj | Zmienna
standaryzowana
| F ( Ui) | pi | n pi | ni - n pi | (ni - n pi)² | | |
2000 | -1,34 | 0,090 1 | 0,090 1 | 3,874 3 | +1,125 7 | 1,268 | 0,33 | |
2800 | -0,68 | 0,248 3 | 0,158 2 | 6,802 6 | -0,802 6 | 0,644 | 0,95 | |
3600 | -0,02 | 0,492 0 | 0,243 7 | 10,479 1 | +0,520 9 | 0,271 | 0,03 | |
4400 | 0,64 | 0,738 9 | 0,246 9 | 10,616 7 | -2,616 7 | 6,849 | 0,65 | |
5200 | 1,30 | 0,903 2 | 0,164 3 | 7,064 9 | +0,935 1 | 0,874 | 0,12 | |
6000 | - | 1,000 0 | 0,096 8 | 4,205 4 | +0,794 6 | 0,631 | 0,15
| |
zatem nie ma podstaw do odrzucenia hipotezy H0, że rozkład przebiegów ogniw gąsienicy do chwili uzyskania zużycia przegubu o wartości 3,5 jest rozkładem normalnym.
Podczas realizacji obliczeń oszacowano dwa parametry hipotetycznego rozkładu normalnego: wartość średnią X oraz wariancję S² (odchylenie standardowe S). Ze względu na konieczność skorzystania z tablic rozkładu normalnego N(0, 1), standaryzowano zmienną losową X uzyskując wartości zmiennej losowej standaryzowanej Ui
zaś suma wartości w ostatniej kolumnie wyznacza wartość statystyki (funkcji testowej) χ², która przy prawidłowości hipotezy H0 ma rozkład λ Kołmogorowa niezależny od postaci hipotetycznej dystrybuanty F( x ).
Dla ustalonego z góry poziomu istotności α należy odczytać z granicznego rozkładu λ Kołmogorowa wartość graniczną λα. Jeżeli zachodzi relacja
λ < λα
to nie ma podstaw do odrzucenia hipotezy H0, że rozkład badanej cechy ma dystrybuantę o postaci F( x ).
Przykład. Wykorzystanie testu zgodności λ Kołmogorowa do weryfikacji rozkładu będzie przedstawione dla danych empirycznych i założeń z poprzedniego przykładu. Tok obliczeń można przedstawić następująco (tabl. 9.16).
Tablica 9.16. Weryfikacja charakteru rozkładu danych empirycznych za pomocą testu zgodności Kołmogorowa
Końce przedziału
xj | Zmienna standaryzowana
| F ( Ui) | ni | nsi | Fi(xi) | Fi(xi) - F (Ui) | |
2000 | -1,34 | 0,090 1 | 5 | 5 | 0,116 3 | 0,026 2 | |
2800 | -0,68 | 0,248 3 | 6 | 11 | 0,255 8 | 0,007 5 | |
3600 | -0,02 | 0,492 0 | 11 | 22 | 0,511 6 | 0,019 6 | |
4400 | 0,64 | 0,738 9 | 8 | 30 | 0,697 6 | 0,041 13 | |
5200 | 1,30 | 0,903 2 | 8 | 38 | 0,883 7 | 0,019 5 | |
6000 | 1,96 | 0,975 0 | 5 | 43 | 1,000 0 | 0,025 0
| |
Maksymalna różnica dystrybuant (wartość modalna) wynosi
D = 0,0413
zatem statystyka λ ma wartość
λ = D • n½ = 0,0413 • 43 = 0,26845
Z tablic rozkładu λ Kołmogorowa można odczytać wartość graniczną λα, która dla a = 0,05 wynosi l0,05 = 1,358.
Ponieważ
l < l0,05
zatem nie ma podstaw do odrzucenia hipotezy, że badana cecha X populacji generalnej ma rozkład normalny.
Podczas badania równocześnie dwóch cech lub więcej stosuje się modele korelacji i regresji, które pozwalają ocenić związki probabilistyczne pomiędzy tymi cechami. Model analizy korelacji pozwala ocenić siłę zależności, zaś model analizy regresji — jej kształt.
9.7.7. Model analizy korelacji dla dwóch cech
Współczynnik korelacji R między badanymi cechami X i Y jest miarą zdefiniowaną następującym wyrażeniem
|
R = |
cov ( X, Y )
σx σy
| (9.78)
|
i jest unormowany miarą korelacji zmiennych X i Y przyjmującą wartości z przedziału
-1 ≤ R ≤ 1
gdzie: cov(X, Y) - kowariancja zmiennych X i Y, σ1, σ2 - odchylenia standardowe zmiennych X i Y.
Jeżeli R = -1 lub R = l, to między zmiennymi X i Y istnieje ścisła zależność w postaci funkcji liniowej. Jeżeli R = 0, to zmienne są nieskorelowane.
Estymatorem nieobciąźonym i zgodnym dla współczynnika korelacji R populacji generalnej jest współczynnik korelacji uzyskany z obserwacji n par realizacji (xi, yi) badanej próby.
Nieraz może być bardziej wygodne stosowanie równoważnego wyrażenia do obliczenia współczynnika korelacji o postaci
|
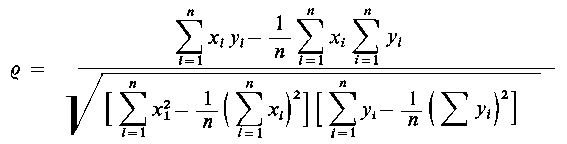
| (9.79)
|
Wartość współczynnika korelacji ρ (oszacowana z próby) jest także wartością losową, jak każdy estymator, dlatego też należy sprawdzić czy rzeczywiście uzyskana wartość współczynnika korelacji bardzo różni się od 0. W tym celu należy postawić hipotezę H0: R = 0 wobec hipotezy alternatywnej H1: R ≠ 0.
Do weryfikacji hipotezy H0 należy policzyć wartość statystyki t-Studenta
|
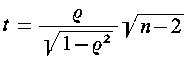
| (9.80)
|
która przy założeniu prawdziwości hipotezy H0 ma rozkład t-Studenta o n-2 stopniach swobody. Odczytując z tablic rozkładu t-Studenta wartość graniczną tα dla założonego poziomu istotności α oraz n - 1 stopni swobody, należy sprawdzić czy zachodzi nierówność
| t | < tα
Jeśli występuje taka zależność, to nie ma podstaw do odrzucenia hipotezy H0, że cechy X i Ysą ze sobą skorelowane w przeciwnym przypadku należy odrzucić hipotezę H0.
Przykład. Podczas badań własności ciernych gum bieżnikowych opon samochodowych uzyskano następujący zbiór wartości współczynnika tarcia µ oraz średnich nacisków jednostkowych próbki q (tabl. 9.17). Sprawdzić czy istnieje korelacja pomiędzy współczynnikiem tarcia µ a średnimi naciskami jednostkowymi q próbki.
Tablica 9.17. Wartości współczynnika tarcia oraz średnich nacisków jednostkowych uzyskane w badaniach gum bieżnikowych|
Badane wielkości | Numer próbki | |
1 | 2 | 3 | 4 | 5 | 6 | 7 | |
Średni nacisk jednostkowy q | 2,427 5 | 3,297 3 | 3,747 0 | 4,475 3 | 4,812 2 | 5,301 1 | 5,622 7 | |
Współczynnik tarcia µ | 0,861 2 | 0,830 5 | 0,799 7 | 0,765 7 | 0,717 6 | 0,694 3 | 0,667 5
| |
Wartość współczynnika korelacji z próby należy obliczyć ze wzoru
|
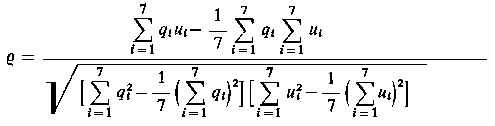
| (9.81)
|
Obliczenia można dokonać za pomocą tabl. 9.18.
Tablica 9.18. Tablica do obliczania współczynnika korelacji pomiędzy współczynnikiem tarcia µ a średnim naciskiem jednostkowym|
i | qi | µi | qi² | µi² | qi µi | |
1 | 2,427 5 | 0,861 2 | 5,892 8 | 0,741 7 | 2,090 6 | |
2 | 3,297 3 | 0,830 5 | 10,872 2 | 0,689 7 | 2,738 4 | |
3 | 3,747 0 | 0,799 7 | 14,040 0 | 0,639 5 | 2,996 5 | |
4 | 4,475 3 | 0,765 6 | 20,028 3 | 0,586 3 | 3,426 7 | |
5 | 4,812 2 | 0,717 6 | 23,157 3 | 0,514 9 | 3,453 2 | |
6 | 5,301 1 | 0,694 3 | 28,101 7 | 0,482 1 | 3,680 6 | |
7 | 5,662 7 | 0,667 5 | 31,614 8 | 0,445 6 | 3,753 2 | |
suma | 29,683 1 | 5,336 5 | 133,707 1 | 4,099 8 | 22,1392
| |
|
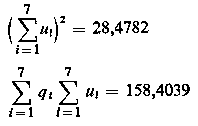
| (9.82)
|
Po podstawieniu tych wartości do wyrażenia na ρ empiryczna wartość współczynnika korelacji z próby wynosi
ρ = -0,9871
Uwzględniając jednak, że współczynnik korelacji z próby jest także zmienną losową, należy zweryfikować hipotezę H0:R = 0 wobec hipotezy alternatywnej H1:R ≠ 0. W tym celu znajdujemy wartość statystyki t-Studenta
|
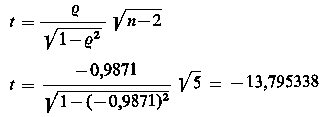
| (9.83)
|
Dla poziomu istotności α = 0,05 znajdujemy wartość krytyczną tα = 2,571 z tablic rozkładu t-Studenta przy r = 5 stopni swobody. Zachodzi więc następująca relacja
13,7953 > 2,571
czyli
| t | < tα
zatem hipotezę H0 należy odrzucić. Oznacza to, że zmienne µ i q są skorelowane. Należy tu dodać, że wartość ρ = -0,9871 sugeruje, że krzywa regresji µ względem q znajduje się blisko funkcji liniowej (rezultaty pomiarów układają się prawie dokładnie na linii prostej), przy czym µ jest malejącą funkcją q.
9.7.8. Estymacja funkcji regresji dla dwóch zmiennych
Najprostszym modelem matematycznym zjawiska w badaniach empirycznych jest funkcja regresji dla dwu cech, której parametry zostają wyznaczone metodą najmniejszych kwadratów dla zaobserwowanych w próbie wartości badanych zmiennych.
Jeżeli podczas obserwacji doświadczenia uzyskano n realizacji (xi, yi) badanych cech X i Y, to na podstawie wykresu rozrzutu punktów empirycznych wykonanego w układzie współrzędnych y-x zakłada się określoną funkcję regresji y(x), która opisuje teoretyczny związek pomiędzy wartościami średnimi cechy Y i cechy X. Zatem każdej zaobserwowanej wartości xi, odpowiada zaobserwowana wartość yi, oraz teoretyczna wartość y(xi) wynikająca z postaci złożonej funkcji regresji. Oszacowanie parametrów dla założonej funkcji regresji metodą najmniejszych kwadratów polega na znalezieniu takich estymatorów, które minimalizują średni błąd kwadratowy odchyleń punktów empirycznych od założonej krzywej regresji y(x), czyli
|
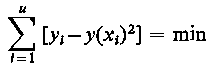
| (9.84)
|
Wynik taki można uzyskać, stosując warunek konieczny i dostateczny do istnienia minimum powyższej funkcji, tzn. badając jej pochodne względem poszukiwanych parametrów funkcji regresji. Powyższy sposób postępowania rozpatrzymy dla prostej regresji, tzn. zakładając następującą funkcję regresji
Parametr nazywa się a współczynnikiem regresji liniowej. Tak więc elementom zbioru zaobserwowanych empirycznych wartości xi zmiennej X można przyporządkować odpowiednie empiryczne wartości yi oraz teoretyczne wartości y(xi) = a xi + b zmiennej Y.
Średni błąd kwadratowy S dla założonej funkcji regresji będzie następujący
|
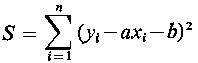
| (9.86)
|
Estymatory dla nieznanych parametrów a oraz b funkcji regresji y(x) powinny zapewnić uzyskanie minimalnej wartości średniego błędu kwadratowego S. W tym celu można zróżniczkować funkcję S względem parametrów a i b, a uzyskane pochodne cząstkowe przyrównać do zera
|
∂ S
∂ a |
= 0
| (9.87)
|
∂ S
∂ b |
= 0
|
czyli
|
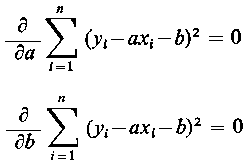
| (9.88a)
| | (9.88b)
|
Stąd po zróżniczkowaniu uzyskamy układ równań liniowych względem a i b
|
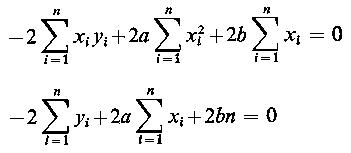
| (9.89a)
| | (9.89b)
|
Rozwiązując powyższy układ równań, znajdujemy estymatory parametrów liniowej funkcji regresji
|
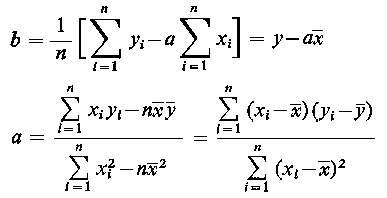
| (9.90a)
| | (9.90b)
|
gdzie x, y - wartości średnie z próby zmiennych X i Y.
W rzeczywistości nie zawsze można skorzystać z liniowej funkcji regresji, ale jest bardzo wiele przypadków, w których funkcje nieliniowe można zamienić na funkcje liniowe wykonując dodatkowe operacje algebraiczne.
Badana jest funkcja regresji w postaci
funkcję tę można zlogarytmować (przy założeniu, że c > 0, a > 0) uzyskując
czyli
gdzie y — lg y, c — lg c, a — lg a.
W celu oszacowania a i c, korzysta się z wyprowadzonych wzorów dla parametrów liniowej funkcji regresji, korzystając przy tym z wyników badań składających się z zaobserwowanych par ( xi, yi), gdzie yi = lg yi. Po wyznaczeniu wartości c i a można określić wartości c oraz a.
Badana jest potęgowa funkcja regresji o postaci
Podobnie jak poprzednio logarytmując tę funkcję, uzyskamy
zaś przyjmując oznaczenia: lg y = y, lg c = c, lg x = x uzyskamy liniową funkcję regresji
W tym przypadku korzysta się więc z empirycznych wartości ( x, y) i postaci zlogarytmowanej xi = lg xi, yi = lg yi
Badana jest logarytmiczna funkcja regresji o postaci
a więc postać liniowej funkcji regresji będzie następująca
gdzie x = lg x.
Do oszacowania parametrów a i b należy zatem uwzględnić materiał doświadczalny zawierający wartości ( xi, yi), gdzie : xi = lg xi, yi = lg yi.
Badana jest funkcja regresji o postaci
funkcję tę przy założeniu x ≠ 0 można sprowadzić do postaci liniowej podstawiając z = 1/x. Otrzymamy wtedy zależność
Do oszacowania parametrów a i b należy zatem uwzględnić wyniki próby ( zi, yi ), gdzie zi = 1/yi.
W pozostałych przypadkach, gdy przyjęta funkcja regresji nie da się przekształcić do postaci liniowej, należy wykorzystać przedstawiony sposób postępowania przy poszukiwaniu estymatorów nieznanych parametrów metodą najmniejszych kwadratów. Badając modele regresji liniowej dla dwu populacji, często konieczne jest ich porównanie. Dobre rezultaty w tym przypadku zapewnia weryfikacja testu dla dwóch współczynników regresji, tzw. testu równoległości. Pozwala on określić podobieństwo modeli regresji dla badanych populacji (a więc i podobieństwo zjawisk probabilistycznych).
Badane są dwie populacje generalne, z których wylosowano dwie próby odpowiednio o licznościach n1 i n2 uzyskując wyniki realizacji cech X i Y w postaci zbiorów par liczb
|
{( x1i, y1i)} | |
{( x2i, y2i)}
|
|
Zakładając liniowe funkcje regresji
|
y1( x ) = a1 x + b1
| (9.101a)
|
|
y2( x ) = a2 x + b2
| (9.101b)
|
należy zweryfikować hipotezę H0: a1 = a2, wobec hipotezy alternatywnej H1: a1 ≠ a2.
Potwierdzenie hipotezy H0 świadczy o tym, że proste regresji y1(x) i y2(x) można uważać za równoległe. W celu zweryfikowania hipotezy H0 należy wyznaczyć parametry funkcji regresji, tj. (a1, b1), (b2, b2) oraz statystykę t-Studenta
|
t = |
a1 - a2
Sa1 - a2
| (9.102)
|
przy czym
|
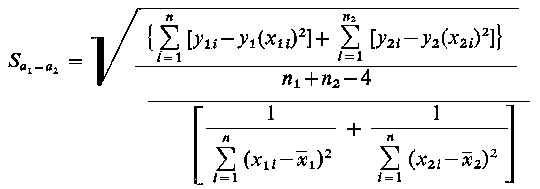
| (9.103)
|
Powyższa statystyka ma przy założeniu prawdziwości sprawdzanej hipotezy H0 rozkład t-Studenta o n1 + n2 - 4 stopniach swobody. Z tablicy tego rozkładu dla ustalonego z góry poziomu istotności oraz n1 + n2 - 4 stopni swobody znajduje się wartość krytyczną tα, tak aby
|
P { |t| ≥ t } = α
| (9.104)
|
Jeżeli zachodzi relacja
to hipotezę H0 o równości współczynników regresji w badanych populacjach należy odrzucić, a w przeciwnym przypadku nie ma podstaw do odrzucenia hipotezy H0 o równoległości porównywanych prostych regresji.
Przykład. Podczas badań własności trakcyjnych opon samochodowych wykonano pomiary współczynnika przyczepności y opony STOMIL oraz PIRELLI przy stałym obciążeniu równym 0,6 MPa, zadając różne wartości obciążenia normalnego na koło. Wyniki pomiarów przy pięciu powtórzeniach podano w tabl. 9.19.
Tablica 9.19. Wyniki pomiarów współczynnika przyczepności φ opon
Obciążenie normalne
Pi
N | Opona STOMIL (symbol l)
współczynnik przyczepności
φ1 ij | Opona PIRELLI (symbol 2)
współczynnik przyczepności
φ2 ij | |
15000 | 0,770 0 | 0,820 0 | 0,773 3 | 0,793 3 | 0,826 7 | 0,750 0 | 0,790 0 | 0,846 7 | 0,770 0 | 0,795 0 | |
20000 | 0,760 0 | 0,772 5 | 0,740 0 | 0,752 5 | 0,758 7 | 0,7175 | 0,727 5 | 0,730 0 | 0,742 5 | 0,732 5 | |
25000 | 0,708 0 | 0,726 0 | 0,744 0 | 0,740 0 | 0,762 0 | 0,682 0 | 0,666 0 | 0,686 0 | 0,678 0 | 0,663 0 | |
30000 | 0,7183 | 0,715 0 | 0,711 7 | 0,716 6 | 0,710 3 | 0,668 3 | 0,658 3 | 0,663 3 | 0,665 0 | 0,671 7
| |
Należy znaleźć funkcje regresji współczynnika przyczepności y względem obciążenia normalnego N oraz zbadać podobieństwo współczynników funkcji regresji dla obu rodzajów opon.
Ze względu na rozkład punktów empirycznych przyjęto, że związek φ(N) wystarczająco dokładnie może być opisany wykładniczą funkcją regresji postaci
gdzie a, c - parametry funkcji regresji
czyli dla opony STOMIL
dla opony PIRELLI
Tego typu funkcje łatwo można linearyzować poprzez ich zlogarytmowanie
|
ln [φ1 ( N )] = ln a1 + c1 N
| (9.107)
| |
ln [φ2 ( N )] = ln a2 + c2 N
|
Przyjmując oznaczenia
|
ln [φ1 ( N )] = φ1 , | |
ln a1 = a1
|
| |
ln [φ2 ( N )] = φ2 , | |
ln a2 = a2
|
otrzymamy następujące liniowe funkcje regresji
|
φ1 = a1 + c1 N
| (9.108a)
| |
φ2 = a2 + c2 N
| (9.108b)
|
Chcąc zatem skorzystać z gotowych wyprowadzonych wzorów na parametry liniowej funkcji regresji, należy zlogarytmować empiryczne wartości φ1ij oraz φ2ij uzyskując wartości wg tabl. 9.20.
Tablica 9.20. Wyniki logarytmowania empirycznych wartości współczynników przyczepności φ1ij i φ2ij|
Obciążenie normalne | opona STOMIL (symbol 1) |
Pi
N | φ1ij = ln φ1ij | |
15 000 | -0,261 343 | -0,198 483 | -0,256 968 | -0,231 410 | -0,190 194 | |
20 000 | -0,274 468 | -0,258 120 | -0,301 178 | -0,284 369 | -0,276 080 | |
25 000 | -0,345 388 | -0,162 563 | -0,295 652 | -0,301 178 | -0,271 705 | |
30 000 | -0,330 881 | -0,335 487 | -0,340 092 | -0,333 184 | -0,338 250 | |
| opona PIRELLI (symbol 2) |
Pi
N | φ2ij = ln φ2ij | |
15 000 | -0,287 593 | -0,235 785 | -0,292 198 | -0,261 343 | -0,229 337 | |
20 000 | -0,332 033 | -0,318 217 | -0,314 763 | -0,297 724 | -0,311 309 | |
25 000 | -0,382 690 | -0,406 406 | -0,376 933 | -0,388 676 | -0,411 011 | |
30 000 | -0,402 952 | -0,418 149 | -0,410 551 | -0,408 018 | -0,398 117
| |
Wartości średnie uzyskane na podstawie tej tablicy wynoszą: φ*1 = 0,286442, φ*2 = 0,342164, N = 2250, zaś parametry liniowych funkcji regresji będą równe
|
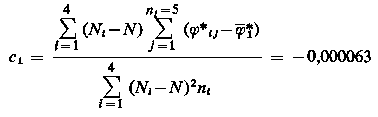
| (9.109)
|
podobnie
|
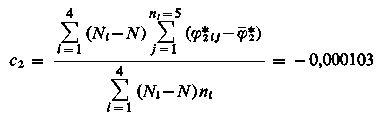
| (9.110)
|
gdzie ni - liczba powtórzeń pomiarów.
Z kolei pozostałe parametry funkcji regresji będą równe
a1 = φ1 - c1 N
a1 = -0,286 442 + 0,000063•2250 = -0,144 692
a2 = φ2 - c2 N
a2 = -0,3422 + 0,000103•2250 = -0,110414
Ponieważ a1 = ln a1, a2 = ln a2, zatem a1 = 0,8653, a2 = 0,8954.
Funkcje regresji współczynnika przyczepności względem obciążenia normalnego N będą miały postać:
- dla opony STOMIL
φ1 = 0,8653 e -0,000063 N
- dla opony PIRELLI
φ2 = 0,8954 e -0,000103 N
Ze względu na losowy rozrzut wyników pomiaru współczynnika przyczepności φ dla dwu krzywych regresji należy wyznaczyć przedziały ufności. Przyjmując wartość α = 0,05, granice przedziałów ufności oraz średnie wartości φ obliczone z funkcji regresji można określić z tabl. 9.21.
Tablica 9.21. Wartości współczynników przyczepności φ wyliczone z funkcji regresjiObciążenie normalne
Pi
N | Opona STOMIL (symbol 1) | Opona PIRELLI (symbol 2) | |
φ1(-) | φ | φ1(+) | φ2(-) | φ2 | φ2(+) | |
15 000 | 0,753 5 | 0,784 8 | 0,816 1 | 0,710 0 | 0,767 5 | 0,825 0 | |
20 000 | 0,753 3 | 0,759 7 | 0,766 1 | 0,718 0 | 0,729 8 | 0,741 6 | |
25 000 | 0,730 9 | 0,737 3 | 0,743 7 | 0,680 3 | 0,692 1 | 0,703 9 | |
30 000 | 0,684 3 | 0,715 6 | 0,746 9 | 0,599 9 | 0,657 4 | 0,714 9
| |
Istnieje duża dokładność przybliżenia funkcji regresji względem wartości empirycznych.
Podane w przykładach programowanie badań trybologicznych oraz analizowanie wyników powinny być przyjmowane jako zasada.
|
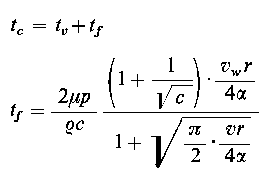
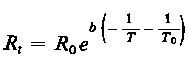
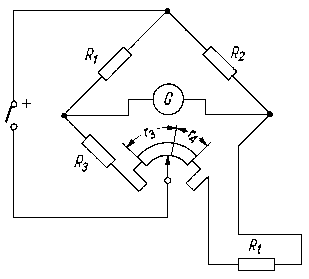
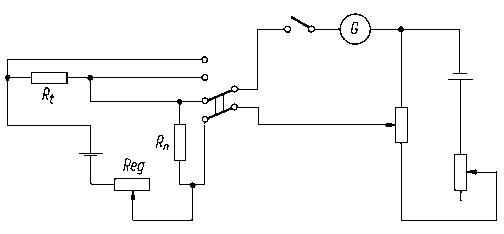
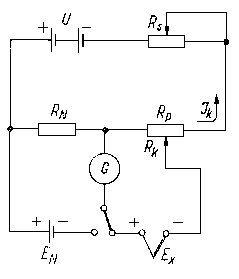
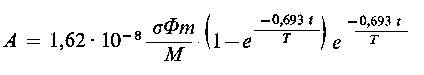
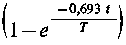- poprawka związana ze zmianą aktywności materiału aktywującego w wyniku jego rozpadu promieniotwórczego w czasie aktywacji, 
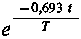- poprawka związana ze zmianą aktywności materiału aktywowanego w wyniku jego rozpadu promieniotwórczego w czasie aktywacji.
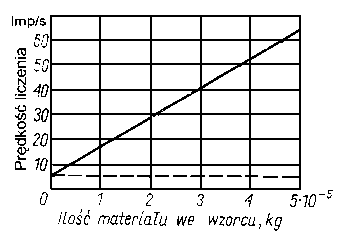
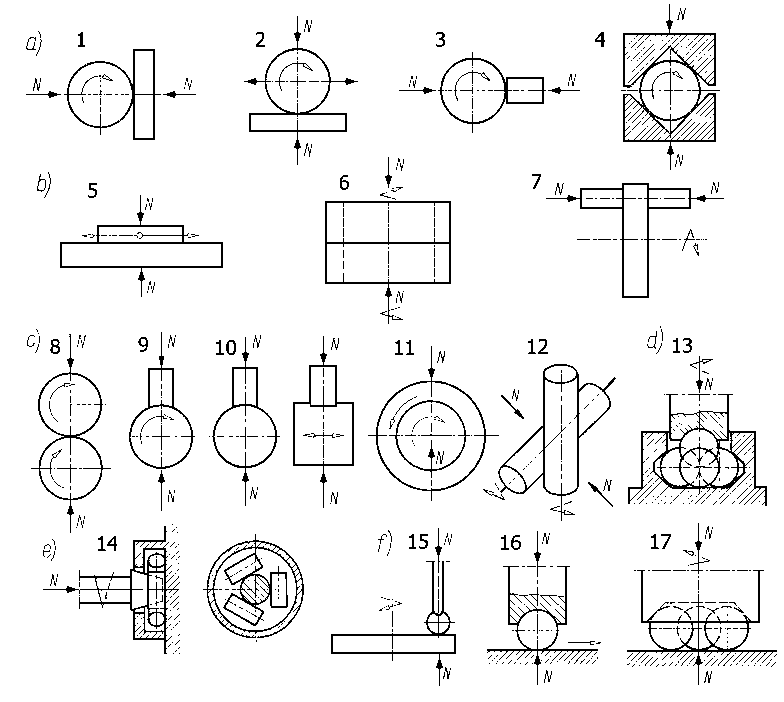
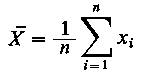
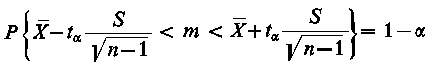
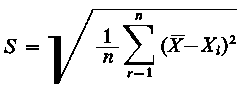
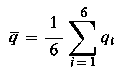
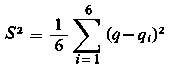
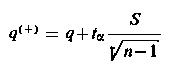
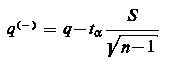
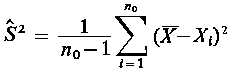
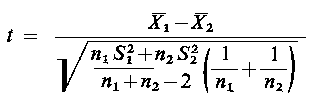
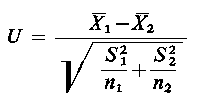
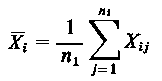
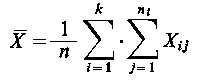
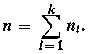