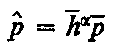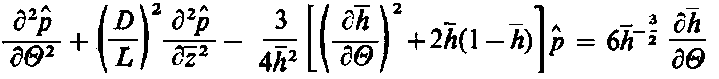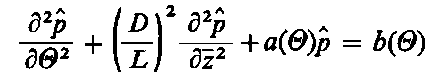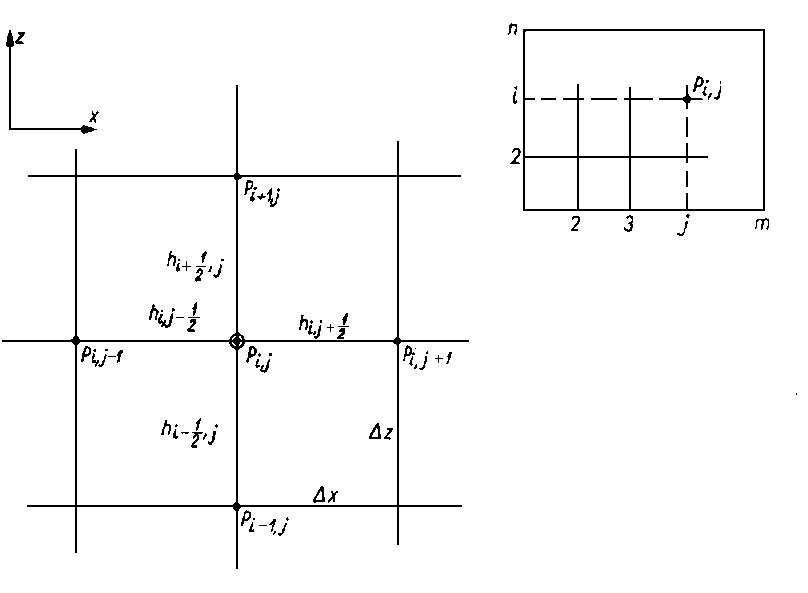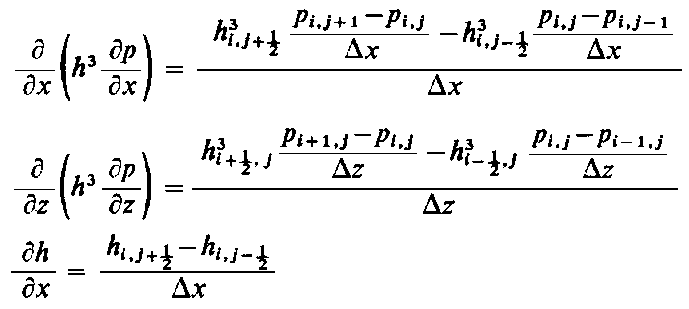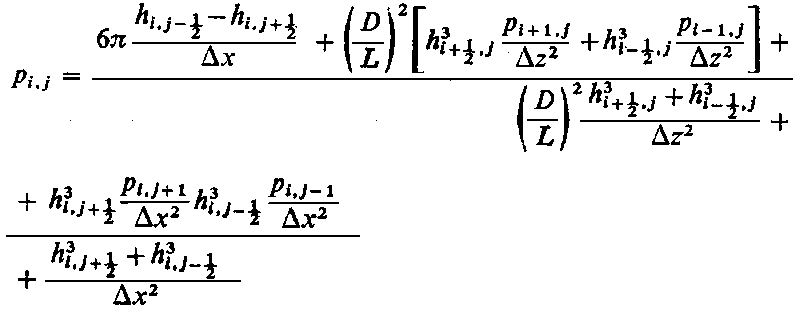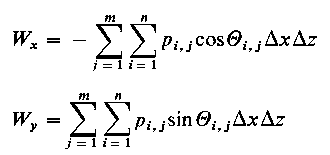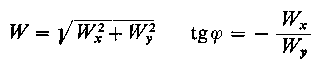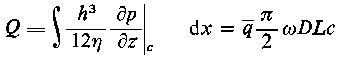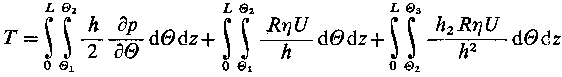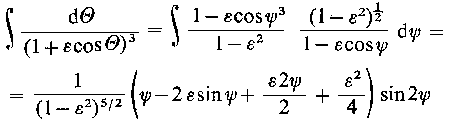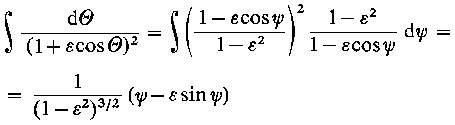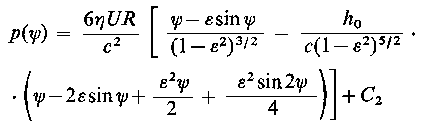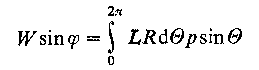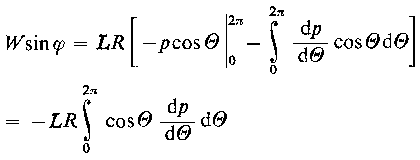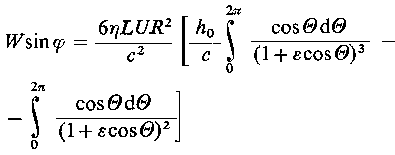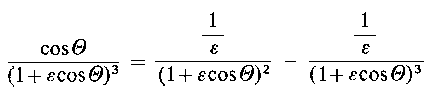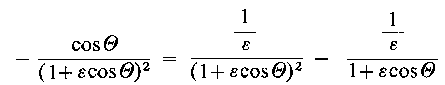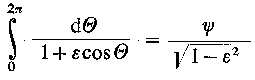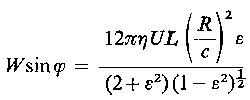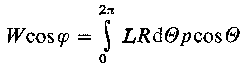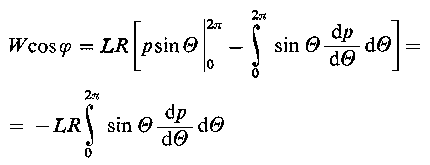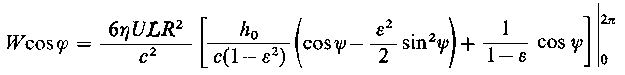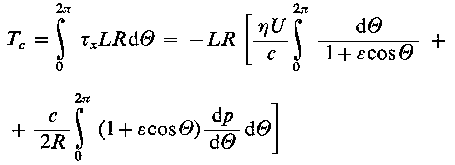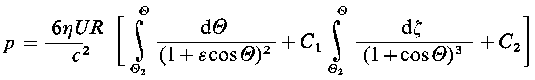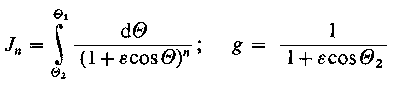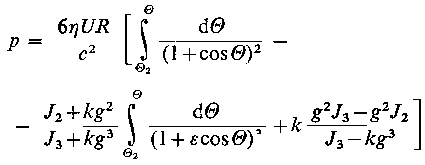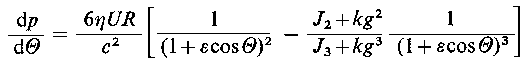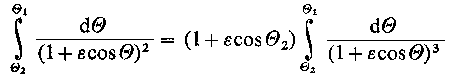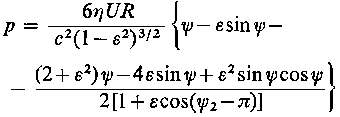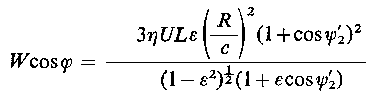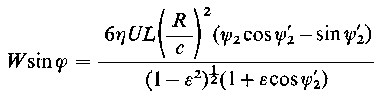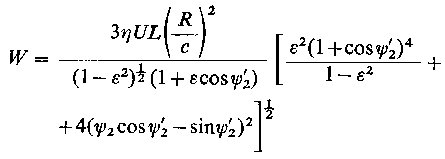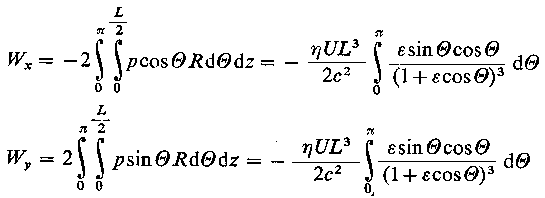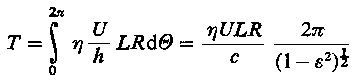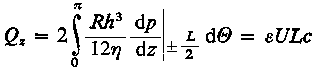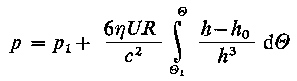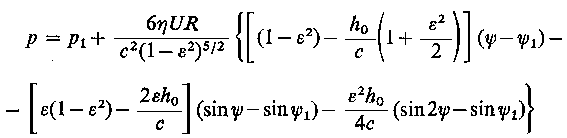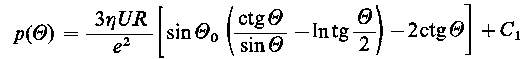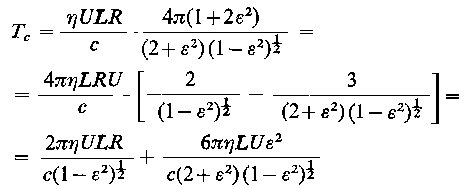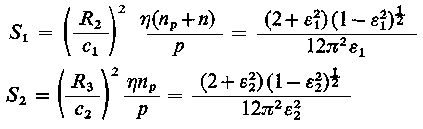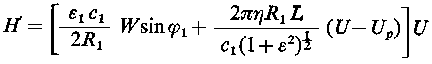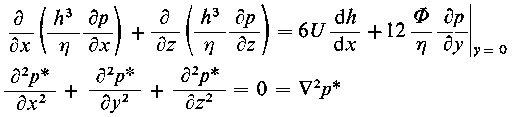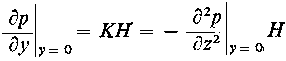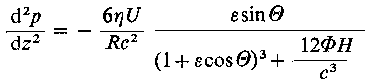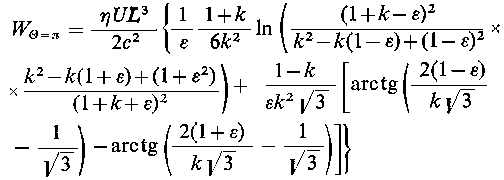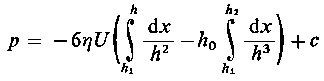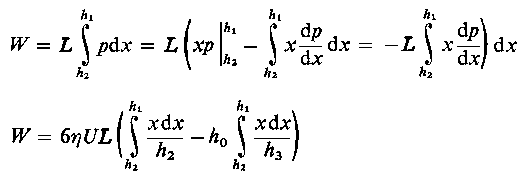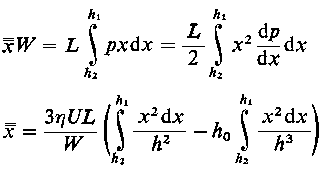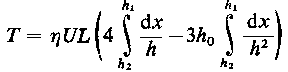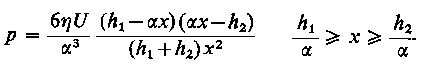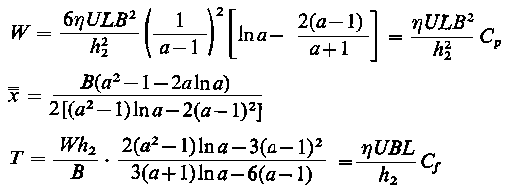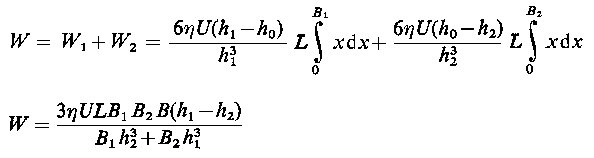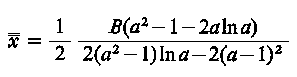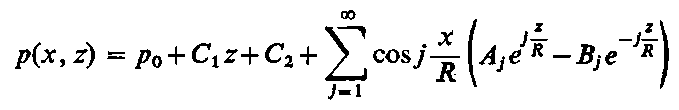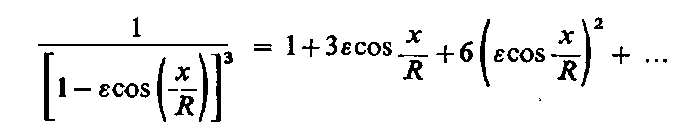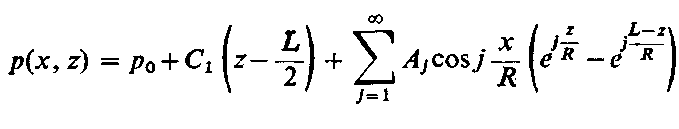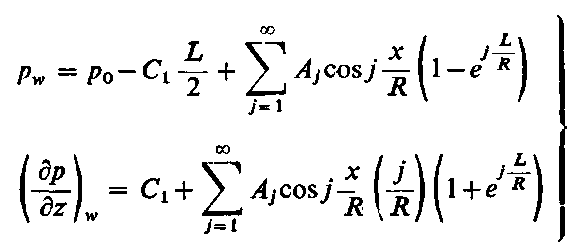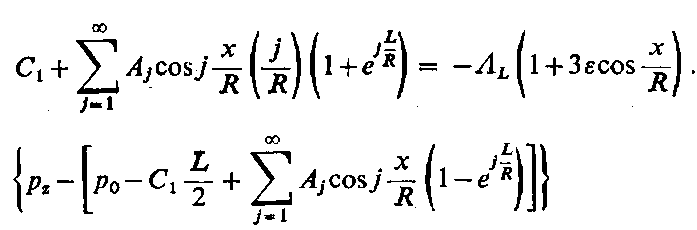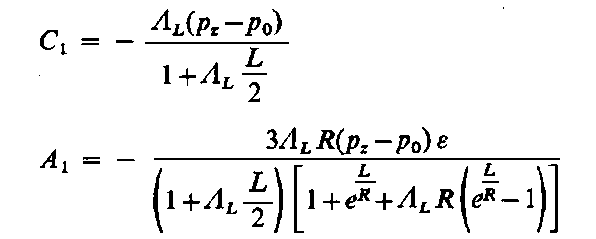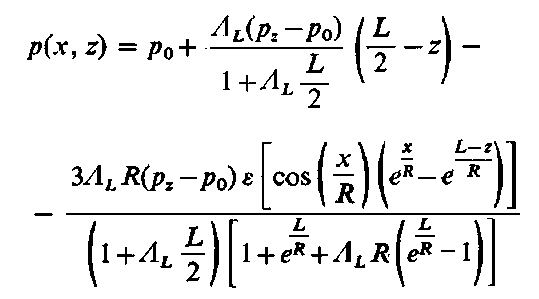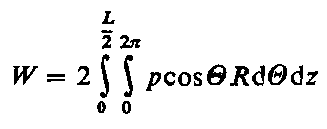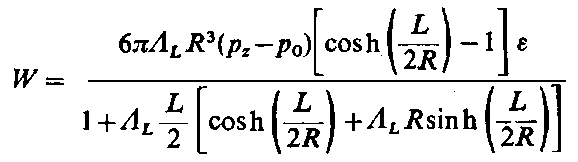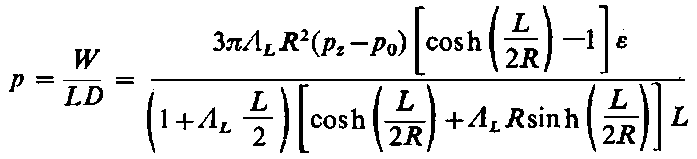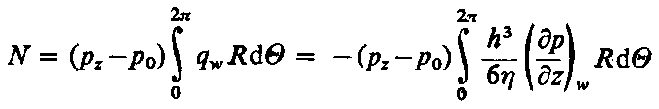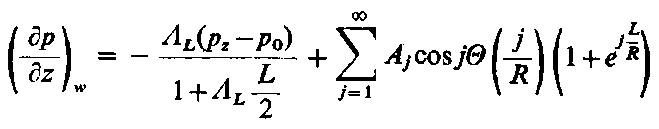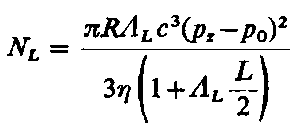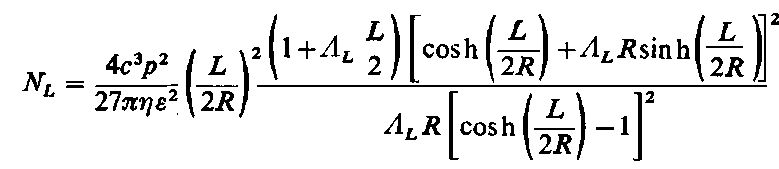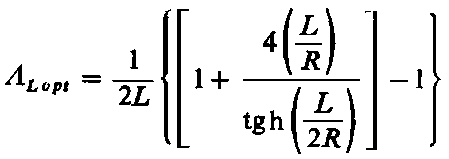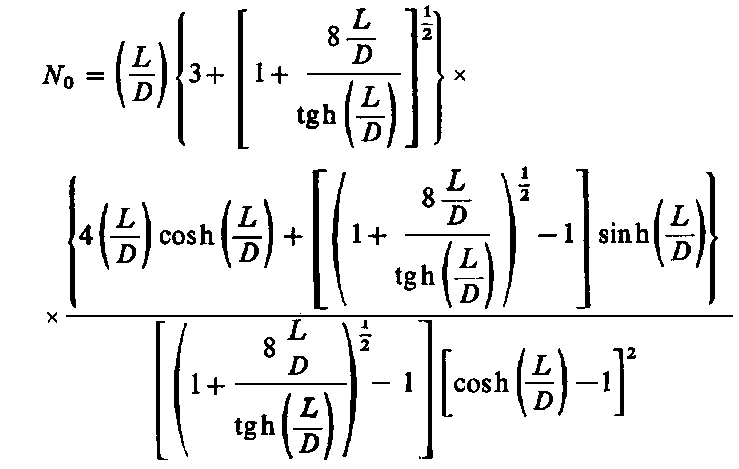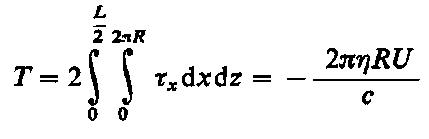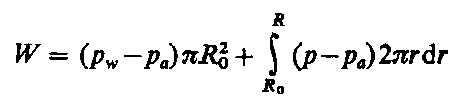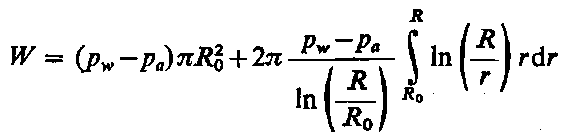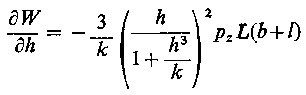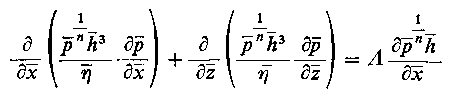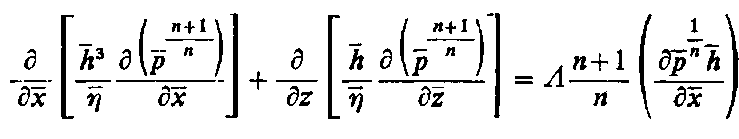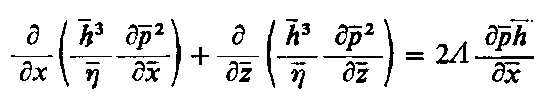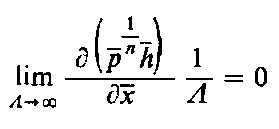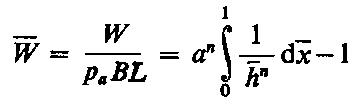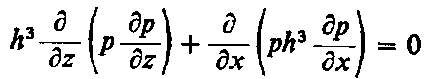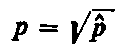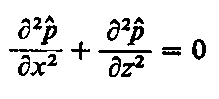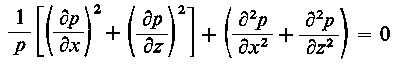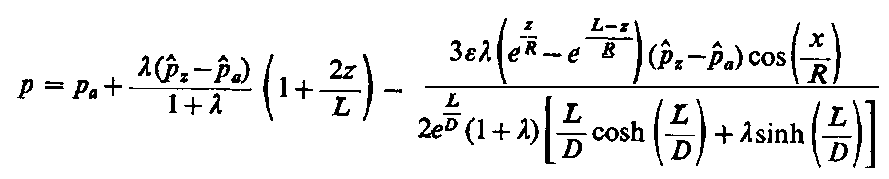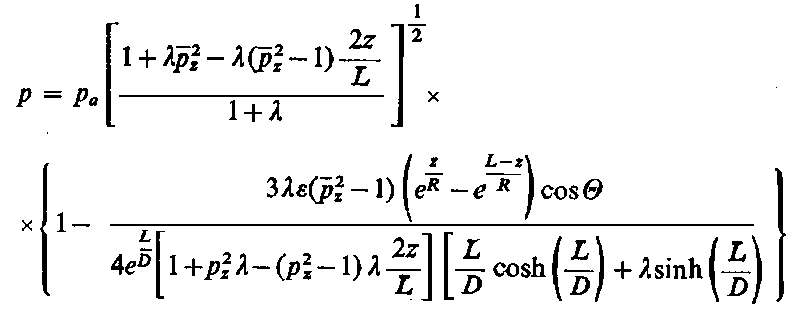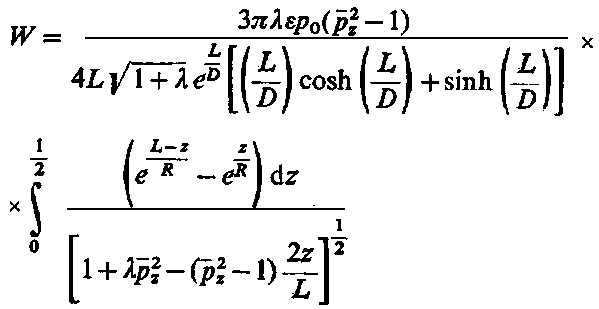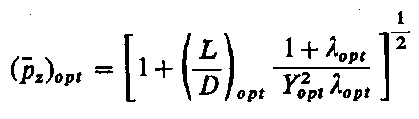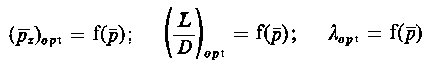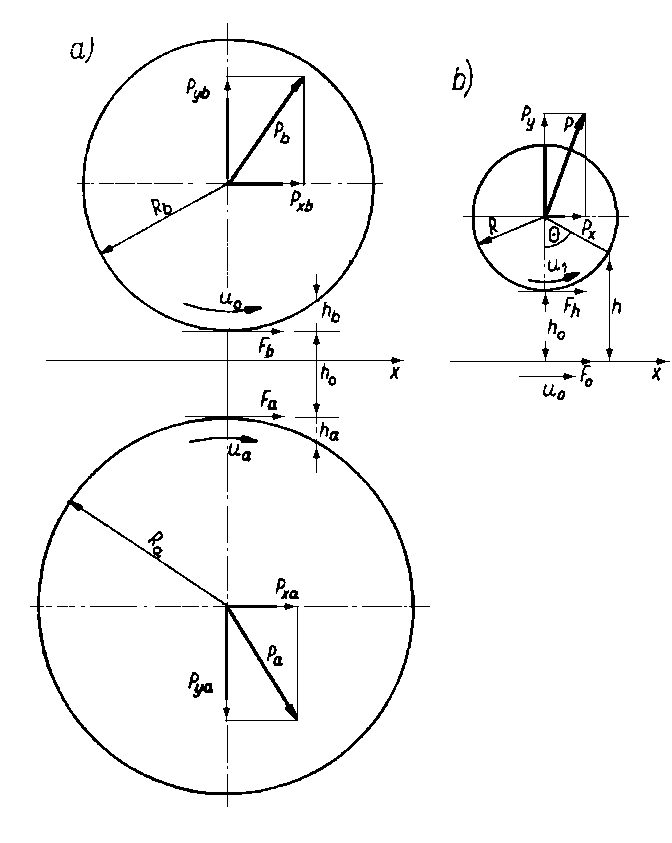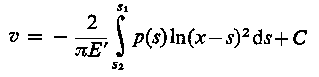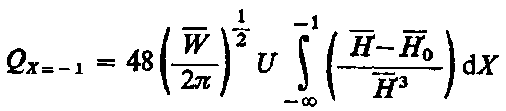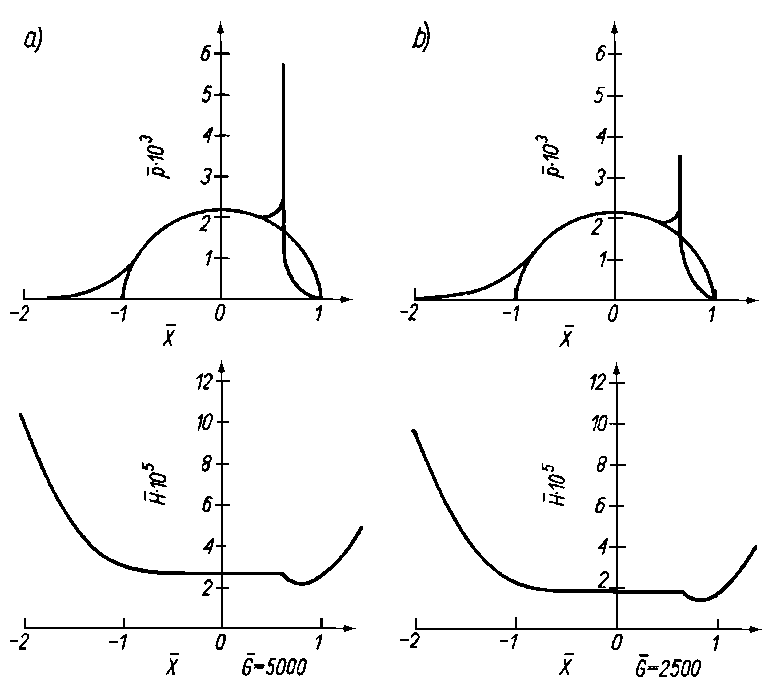| |
6.5.3. Metody analogowe
Metody analogowe są oparte na identyczności równań różniczkowych procesu modelowanego i modelującego. I tak na przykład proces smarowania hydrodynamicznego może być modelowany przez zjawiska jakie zachodzą w kąpieli elektrolitycznej. Wykorzystuje się tu identyczność równania różniczkowego opisującego zależność pomiędzy potencjałem elektrycznym a prądem z jednej strony, a ciśnieniem i przepływem cieczy z drugiej strony. Ogólnie, gęstość przepływu prądu w kierunku dowolnych osi x i z wyraża się następującą zależnością
|
ix = |
H
k |
∂ E
∂ x | |
iz = |
H
k |
∂ E
∂ z
| (6.144)
|
gdzie k - rezystywność, H - przekrój przewodnika.
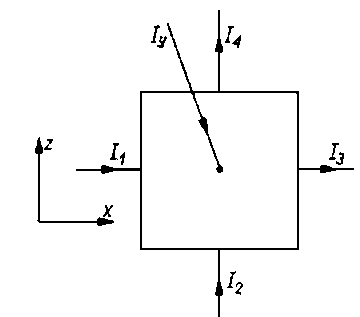 |
Rys. 6.44. Element elektrolitu o dolnej powierzchni nie przewodzącej prądu
|
Zgodnie z rys. 6.44, który przedstawia element elektrolitu o dowolnej powierzchni (płaszczyzna x, z) nie przewodzącej prądu, można napisać
|
I1 + I2 - I3 - I4 + Iy = ix d z + iz d x + |
∂
∂ x |
(ix d z) d x + | |
|
- ix d z - iz d x - |
∂
∂ z |
(iz d x) d z + Iy = 0
| (6.145)
|
Wykorzystując przytoczone uprzednio wyrażenia na gęstość prądu, uzyskuje się
|
∂
∂ x |
( |
H
k |
∂ E
∂x |
) + |
∂
∂ z |
( |
H
k |
∂ E
∂z |
) = Iy |
I
A
| (6.146)
|
gdzie: k - rezystywność, H - wysokość elektrolitu, I - prąd płynący przez powierzchnię A elektrolitu.
Równanie (6.146) ma identyczną postać z równaniem Reynoldsa, jeżeli założyć
|
H
k |
≈ |
h³
η | |
Iy ≈ 6 U |
d h
d x
| (6.147)
|
Równanie (6.146) jest więc analogiem zjawiska smarowania hydrodynamicznego. Jeżeli więc sporządzić kąpiel elektrolityczną, w której spełnione będą powyższe zależności, to potencjał E w dowolnym punkcie elektrolitu będzie odpowiadał ciśnieniu p w łożysku. Dla stałych wartości k oraz h powyższe zależności przyjmują postać
|
H ≈ h³ | |
I k
A |
≈ 6 η U |
d h
d x
| (6.148)
|
Na rys. 6.45 przedstawiono analog, w którym głębokość elektrolitu jest proporcjonalna do h³, zaś prąd w każdym elemencie pola A jest proporcjonalny do 6ηU(d h/d x). Model ten wytwarza potencjały E proporcjonalne do rozkładu ciśnienia istniejącego w łożysku.
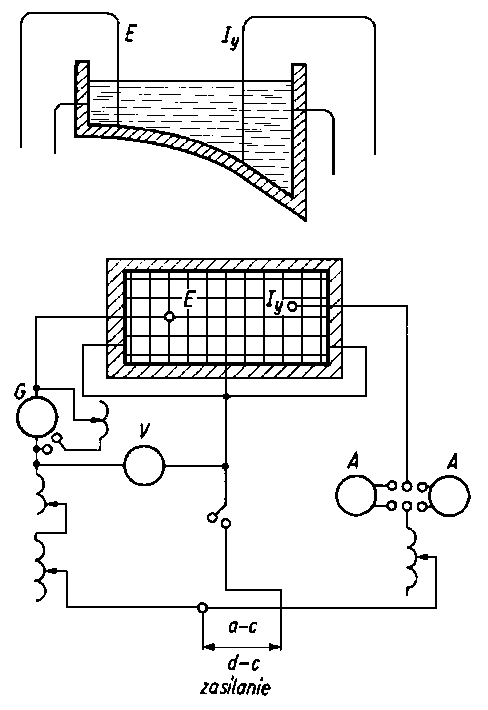 |
Rys. 6.45. Elektryczny analog smarowania hydrodynamicznego z przepływem prądu w elektrolicie;
G - generator,
V - woltomierz,
A-A - regulator natężenia prądu,
E - siła elektromotoryczna
|
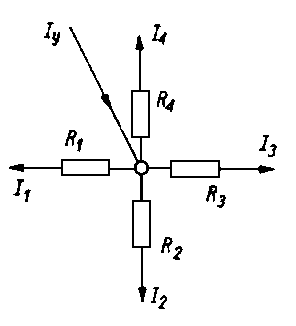 |
Rys. 6.46. Elektryczny analog smarowania hydrodynamicznego z przepływem prądu w sieci złożonej z oporników
|
Innym interesującym analogiem smarowania hydrodynamicznego jest sieć elektryczna prądu stałego. Element takiej sieci jest przedstawiony na rys. 6.461 Ciśnienie jest tu symulowane przez napięcie i natężenie przepływu cieczy przez prąd. Opór przepływu jest reprezentowany przez oporniki. Stosując do węzła prawo Kirchhoffa otrzymuje się
| |
I = I1 + I2 + I3 + I4 = |
E0 - E1
R1 |
+ |
E0 - E2
R2 |
+ |
E0 - E3
R3 |
+ |
E0 - E4
R4
| (6.149)
|
a stąd
Drugi składnik prawej strony równania (6.153) całkowany jest w granicach od 0 do Z,. W zasadzie jest to nieprawdziwe, ponieważ począwszy od punktu E, a więc od punktu θ2, następuje rozdzielenie warstewki cieczy. Na skutek tego łożysko nie jest pokryte smarem na całej swojej długości L, lecz tylko na długości L' < L. Długość L łatwo można obliczyć ponieważ począwszy od θ2 gradient ciśnienia jest równy zeru, nie występują więc upływy boczne.
W zakresie od θ2 do θ3 stosuje się elementarne równanie ciągłości przepływu
| |
U
2 |
L h2 = |
U
2 |
L' h
| (6.154)
|
gdzie h2 - grubość warstewki, przy której nastąpiło rozdzielenie przepływu.
Z równania tego można obliczyć
6.5.4. Wyniki analizy smarowania hydrodynamicznego
Wyznaczony na podstawie teorii hydrodynamicznej rozkład ciśnienia p ( θ, z ) jest najważniejszą charakterystyką łożyska ślizgowego. Stanowi on podstawę do obliczenia pozostałych parametrów. W przypadku łożyska ślizgowego z pełną panwią, podstawowymi parametrami są:
e - mimośrodowość względna,
S - liczba Sommerfelda,
qz - jednostkowe natężenie przepływu w kierunku osi z,
| ( |
R
c
| ) f | - względny współczynnik tarcia, |
p0
pśr | - stopień spiętrzenia ciśnienia,
|
j - kąt usytuowania linii działania obciążenia.
Uzyskany za pomocą jednej z podanych metod rozkład ciśnienia p pozwala wyznaczyć odpowiednie wyrażenie na siłę obciążenia (oś θ = 0 pokrywa się z osią y )
| |
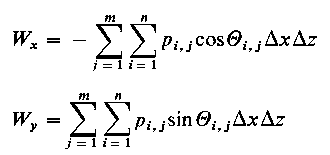
| (6.156)
|
skąd
| |
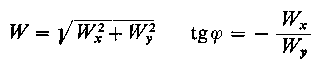
| (6.157)
|
Natężenie przepływu można obliczyć z równania (6.152)
| |
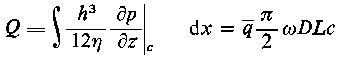
| (6.158)
|
Po uwzględnieniu powyższego równanie na straty tarcia (6.153) przyjmie postać
| |
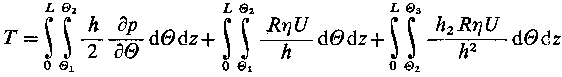
| (6.159)
|
Charakteryzując prace łożyska ściśle pasowanego o maksymalnej nośności przy znanej grubości warstwy oleju, w tabl. 6.10 podano wartości parametrów, przy których uzyskuje się minimum siły tarcia.
Tablica 6.10. Optymalne warunki pracy łożysk ściśle pasowanych|
β, ° | 30 | 60 | 90 | 120 | 150 | |
θ ° | 129,1 | 92,2 | 64,3 | 40,7 | 19,4 | |
α | 17,5 | 35,8 | 55,7 | 77,7 | 101,1 | |
α/β | 0,58 | 0,59 | 0,62 | 0,65 | 0,67 | |
h1/hmin | 2,18 | 2,14 | 2,08 | 2,0 | 1,80 | |
e/h | 2,18 | 2,14 | 2,31 | 3,02 | 5,43 | |
h0/hmin | 1,4 | 1,48 | 1,62 | 1,84 | 2,13 | |
θ0, ° | 150,1 | 136,4 | 135,2 | 142,4 | 156,9 | |
F, ° | 56,6 | 38 | 30 | 28,4 | 30,5 | |
| 0,00451 | 0,01685 | 0,03309 | 0,04534 | 0,03924 | |
| 0,0407 | 0,0774 | 0,1073 | 0,1284 | 0,1339 | |
| 9,027 | 4,597 | 3,242 | 2,831 | 0,3413
| |
W celu zorientowania w tendencjach zmian wartości podstawowych parametrów pracy łożyska przedstawiono na rys. 6.47 w skali logarytmicznej modelowo zależności obciążenia od prędkości obrotowej sześciu rodzajów łożysk:
- - łożysko niesmarowane,
- - łożysko toczne,
- - łożysko hydrostatyczne,
- - łożysko hydrodynamiczne, zasilane smarem pod ciśnieniem (ciągła wymiana oleju),
- - łożysko hydrodynamiczne samosmarowne (bez obiegu wymiany oleju),
- - łożysko porowate.
Krzywe W = W( n ) ograniczają na płaszczyźnie (W, n) obszar bezpiecznej pracy łożyska. Stanowią one granicę, powyżej której zaczynają występować zjawiska uniemożliwiające właściwy przebieg smarowania hydrodynamicznego. Zależności te uwzględniają dodatkowe ograniczenia związane ze smarowaniem rzeczywistych elementów. I tak na rys. 6.47d uwzględniono ograniczenie w zakresie obciążalności, związane z grubością warstwy oleju, a wynikające z istnienia chropowatości współpracujących powierzchni. Tego nie przewiduje klasyczna teoria hydrodynamiczna. Zagięcie krzywej opisuje inne ograniczenie-zmniejszenie obciążalności na skutek wpływu szybkości ścinania na lepkość. Wpływ ten można uwzględnić, wprowadzając do równań założoną funkcję lepkości.
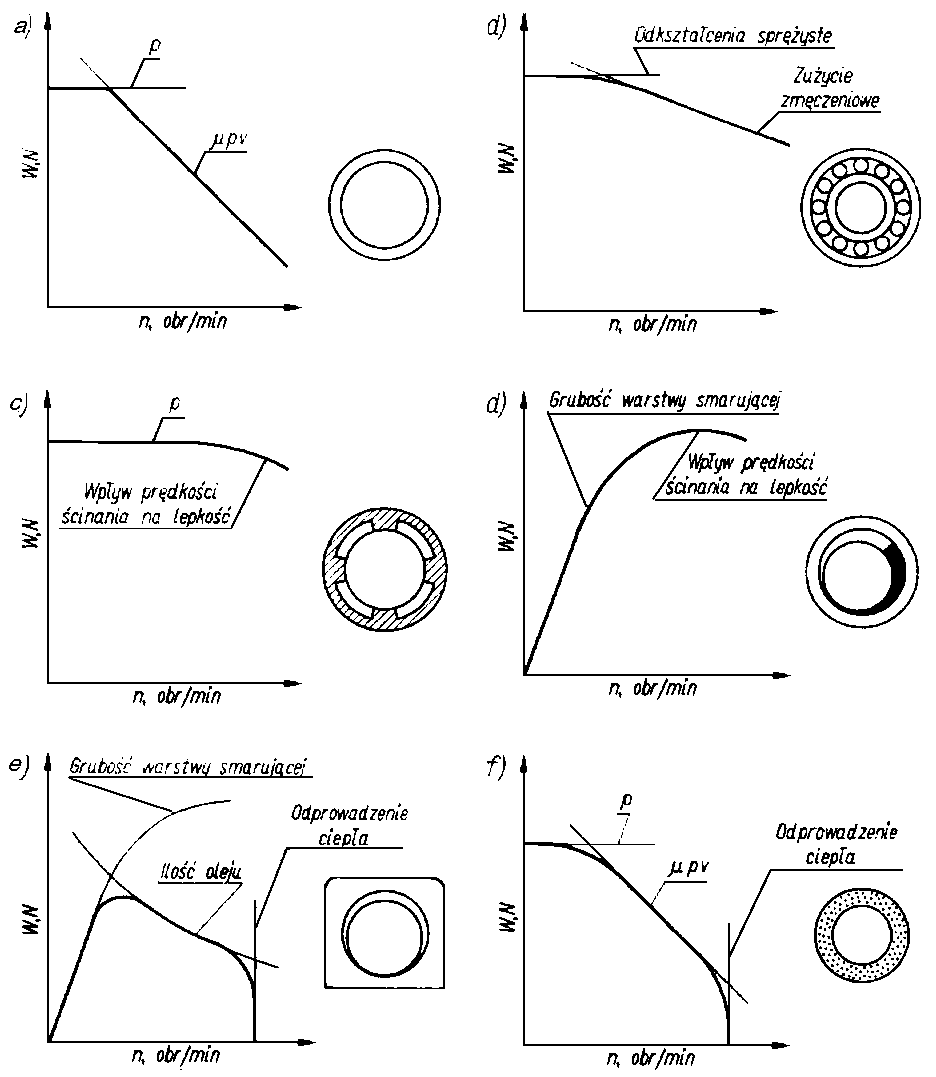 |
Rys. 6.47. Modele zależności obciążenia od prędkości obrotowej łożysk ślizgowych:
- łożysko niesmarowane,
- łożysko toczne,
- łożysko hydrostatyczne,
- łożysko hydrodynamiczne z zasilaniem,
- łożysko hydrodynamiczne bez zasilania,
- łożysko porowate,
W- obciążenie w N,
n - prędkość obrotowa obr/min,
p - nacisk jednostkowy w Pa,
v - prędkość w m/s,
µ - współczynnik tarcia
|
Podobne ograniczenia występują w łożysku samosmarownym (rys. 6.47e). Obciążalność jest tu dodatkowo zmniejszona, ponieważ w wytwarzaniu ciśnienia hydrodynamicznego bierze udział jedynie jednorazowo zalana do łożyska porcja oleju. Nie jest ona uzupełniana ciągle w wyniku obiegu oleju jak w przypadku łożyska wg rys. 6.47d. Brak wymiany oleju wpływa także na większe obciążenia cieplne łożyska, dlatego też ograniczenie obciążalności jest spowodowane możliwością odprowadzenia ciepła przez obudowę.
Dla porównania na rys. 6.47a przedstawiono charakterystykę łożyska niesmarowanego, na rys. 6.47b - charakterystykę łożyska tocznego, na rys. 6.47c - charakterystykę łożyska hydrostatycznego, a na rys. 6.47f-charakterystykę łożyska porowatego.
Przykłady ilościowych charakterystyk łożysk poprzecznych i wzdłużnych smarowanych hydrodynamicznie przedstawiono na rys. 6.48 i 6.49. Dla celów
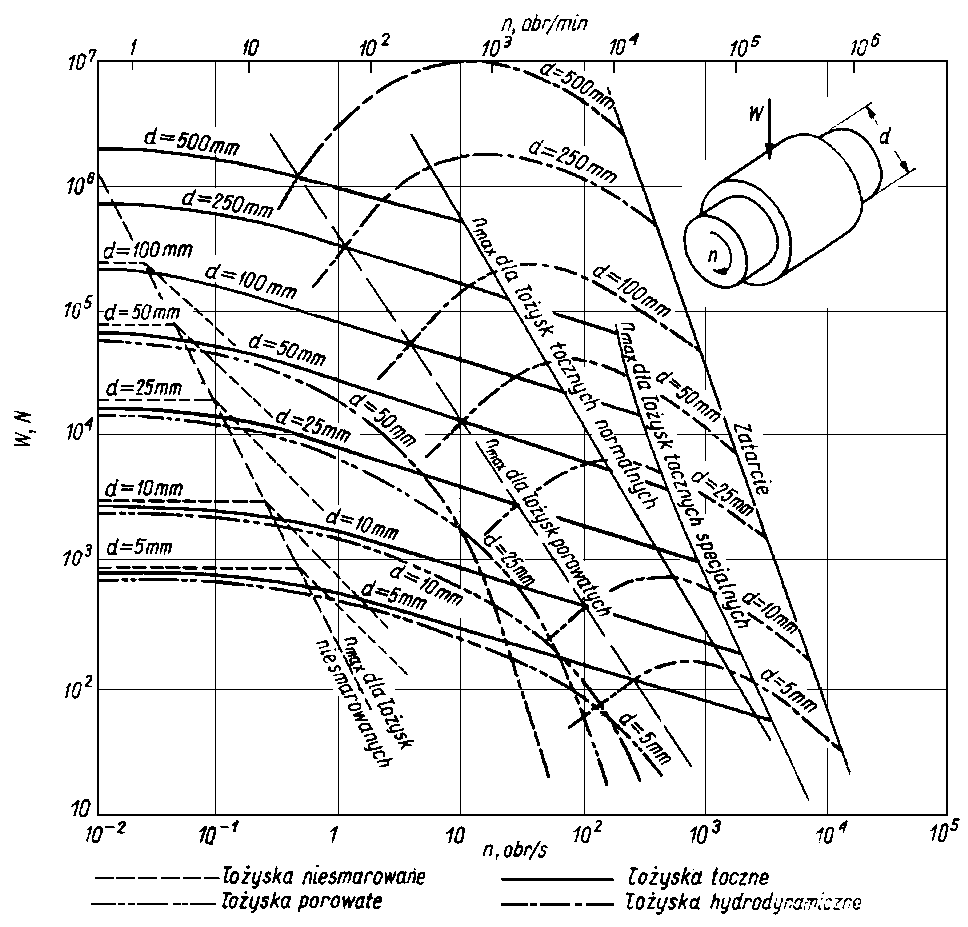 | |
Rys. 6.48. Charakterystyki łożysk poprzecznych smarowanych hydrodynamicznie
|
porównawczych naniesiono na nie także krzywe dotyczące pozostałych rodzajów łożysk. Rodziny krzywych dotyczące poszczególnych rodzajów łożysk odpowiadają swoim kształtem zależnościom modelowym z rys. 6.47. Wykresy przedstawione na rys. 6.48 i 6.49 wiążą ze sobą wymiary geometryczne, prędkość obrotową i obciążenie łożyska. W przypadku łożysk hydrodynamicznych obowiązują one oczywiście dla ściśle określonych wartości luzu oraz lepkości oleju. Wartości luzu i lepkości odpowiadające przytoczonym charakterystykom naniesiono na rys. 6.50 i 6.51. Ponieważ obciążalność łożyska porowatego zależy od jego porowatości, przytoczono też, dla tego typu łożyska, zakresy jego pracy w zależności od porowatości i sposobu smarowania (rys. 6.52).
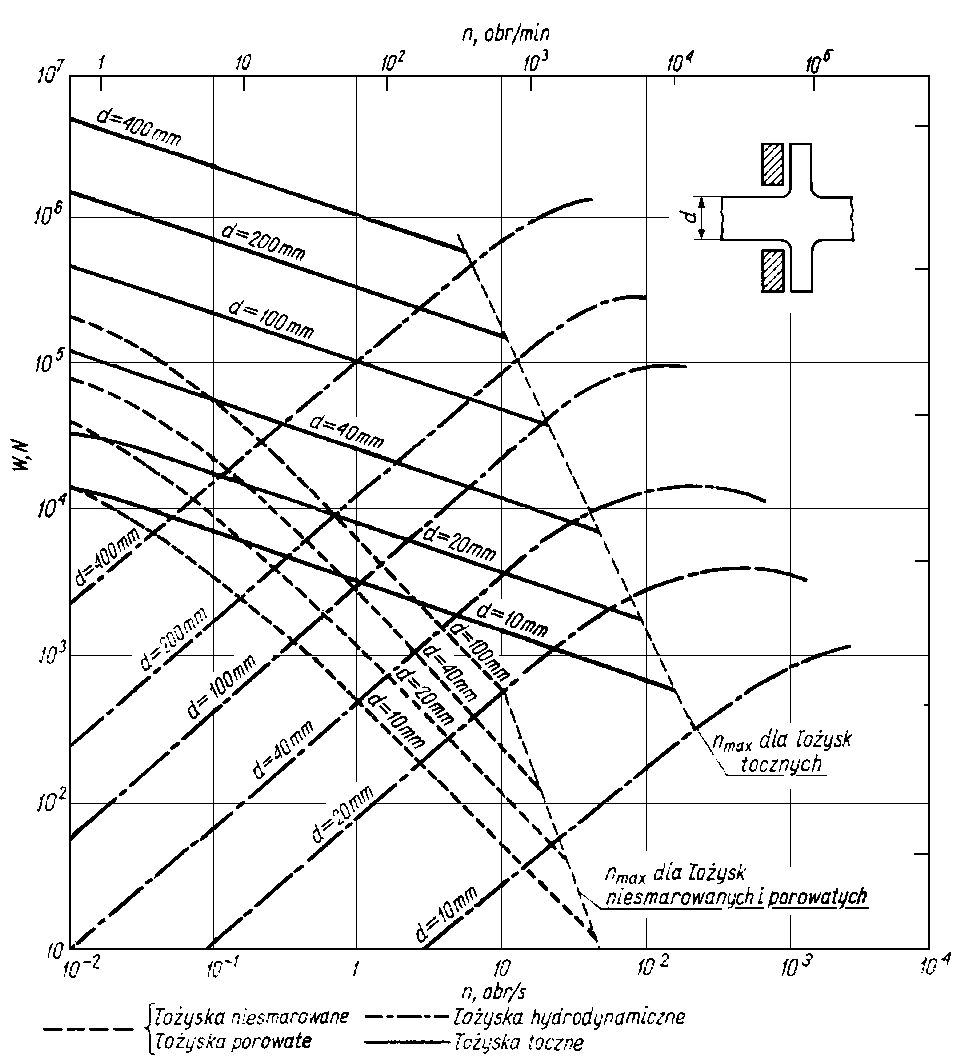 | |
Rys. 6.49. Charakterystyki łożysk wzdłużnych smarowanych hydrodynamicznie
|
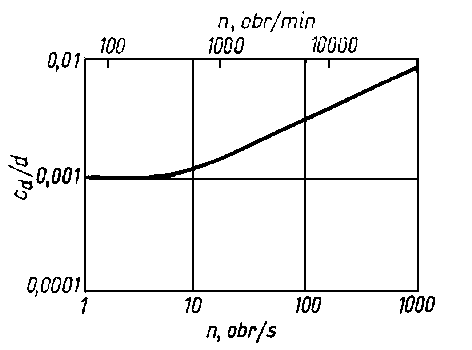
Rys. 6.50. Zależność zalecanej orientacyjnie wartości luzu względnego cd / d łożyska poprzecznego od prędkości obrotowej n czopa
|
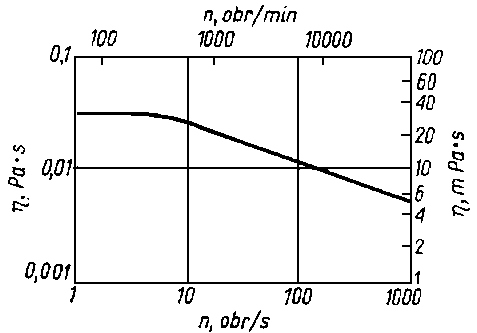
Rys. 6.51. Zależność zalecanej orientacyjnie lepkości dynamicznej η oleju od prędkości obrotowej n czopa
|
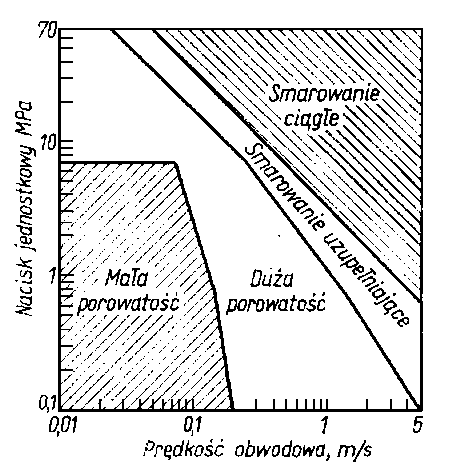 |
Rys. 6.52. Zakresy pracy łożyska porowatego
|
6.6. Łożyska poprzeczne i wzdłużne smarowane hydrodynamicznie
6.6.1. Łożyska poprzeczne jednowymiarowe
Jeżeli uczynić założenie, że łożysko jest nieskończenie długie w kierunku osiowym, to wynika z tego brak zmian ciśnienia w kierunku osi z, tzn. dp/dz = 0. Równanie (6.99) przyjmie więc następującą postać
|
d
d x |
( |
h³
η |
d p
d x |
) = 6 U |
d h
d x
| (6.160)
|
Jeżeli natomiast pominąć przepływ cieczy w kierunku osi x spowodowany gradientami ciśnienia, podobnie jak w krótkich łożyskach (zachowując część przepływu wynikającą ze ścinania), to
|
∂
∂ x |
h³
η |
∂ p
∂ x |
= 0
| (6.161)
|
zaś równanie (6.99) przyjmie postać
|
∂
∂ z |
h³
η |
∂ p
∂ z |
= 6 U |
d h
d x
| (6.162)
|
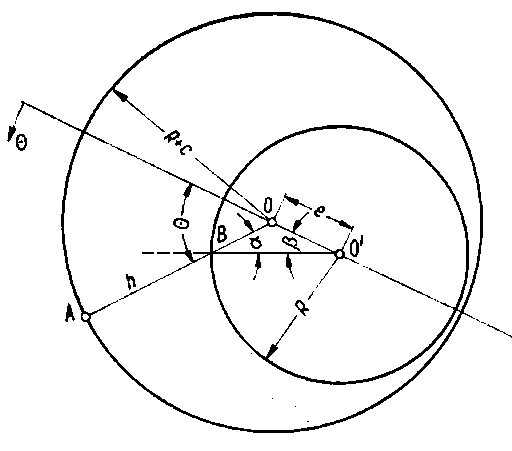 |
Rys. 6.53. Wielkości geometryczne charakteryzujące kształt warstwy cieczy w szczelinie o grubości h
|
Równania powyższe są określone z wyjątkiem funkcji h. W przypadku łożyska wzdłużnego postać funkcji h jest różna w zależności od kształtu ślizgających się powierzchni. Dla łożysk poprzecznych funkcja ta ma jedną uniwersalną postać. Można ją określić na podstawie rys. 6.53, z którego wynikają następujące zależności
|
OB = R [1 - (e/R)²]½ - e cos θ
| (6.163)
|
ponieważ e/R « 1 oraz h = R + c - OB
Przyjmując x = R θ i zakładając, że η = const, uzyskuje się następującą postać równania
|
d
d θ |
h³ |
d p
d θ |
= 6 η U R |
d h
d θ
| (6.164)
|
Całkując to równanie względem θ otrzymuje się
|
d p
d θ |
= 6 η U R |
h + C1
h³
| (6.165)
|
a dla C1 - h0
|
d p
d θ |
= 6 η U R |
h - h0
h³
| (6.166)
|
gdzie h - określone przez równanie (6.133), h0 - nadal nieznane.
Podstawiając do równania (6.164) wyrażenie na h oraz całkując je względem θ można otrzymać rozkład ciśnienia p określony zależnością
| |
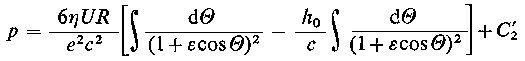
| (6.167)
|
W celu scałkowania powyższego równania Sommerfeld wprowadził pomocniczą zmienną ψ występującą we wzorze
|
1 + ε cos θ = |
1 - ε²
1 - ε cos ψ
| (6.168)
|
z którego wynika
|
cos θ = |
cos ψ - ε
1 - ε cos ψ
| (6.169)
|
Stosując
można obliczyć
|
sin θ = |
(1 - ε²)½ sin ψ
1 - ε cos ψ
| (6.170)
|
Różniczkując wyrażenie na sin θ względem ψ i korzystając z wyrażenia na cos θ (lub odwrotnie) otrzymuje się
|
d θ = |
(1 - ε²)½ d ψ
1 - ε cos ψ
| (6.171)
|
Wartości graniczne θ = 0 oraz θ = 2π transformują się na takie same dla współrzędnej ψ : stąd warunki brzegowe, tzw. warunki brzegowe Sommerfelda są następujące
Całkując składniki wyrażenia na rozkład ciśnienia p uzyskuje się
| |
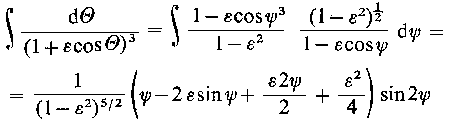
| (6.173a)
|
oraz
| |
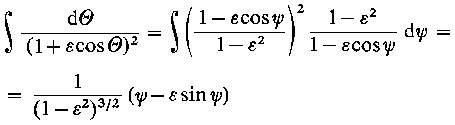
| (6.173b)
|
stąd po podstawieniu p ( θ ) Ű p ( ψ )
| |
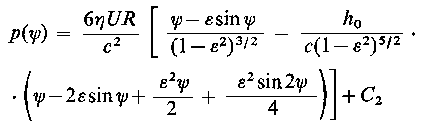
| (6.174)
|
Korzystając z pierwszego warunku brzegowego można określić
C2 = pa
Wykorzystując drugi warunek brzegowy można obliczyć
|
h0 = |
2 c (1 + ε²)
2 + ε²
| (6.175)
|
Po podstawieniu wyrażeń na C2 i h0 oraz po transformacji na układ współrzędnych ( R, θ), równanie na rozkład ciśnienia przyjmie następującą postać
|
p = pa + |
6 η U R ε
c² |
(2 ε cos θ) sin θ
(2 + ε²)(1 + ε cos θ)²
| (6.176)
|
Ciśnienie pa można obliczyć z warunków istniejących w punkcie B gdzie dane ciśnienie wlotowe p1 odpowiada określonemu kątowi θ. Jeżeli otwór zasilający znajduje się w punkcie θ1 = 0, wówczas oczywiście wartość pa jest równa ciśnieniu wlotowemu p1.
Równanie (6.176) przewiduje również obszary wysokich ciśnień ujemnych, jak to przedstawiono na rys. 6.54.
Wielkość ujemnych ciśnień zależy zarówno od położenia θ1, jak i od wartości ciśnienia wlotowego p1. W każdym jednak przypadku rozkład ciśnienia jest funkcją nieparzystą względem linii θ1 = π oraz p = pa
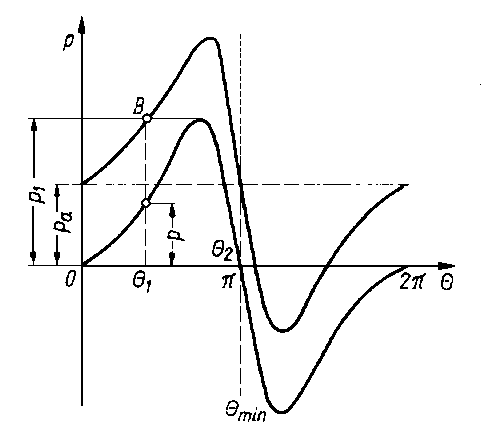 |
Rys. 6.54. Teoretyczny rozkład ciśnienia w szczelinie łożyska poprzecznego (warunki brzegowe Sommerfelda)
|
Składową pionową obciążenia można określić przez całkowanie równania na p po powierzchni łożyska
| |
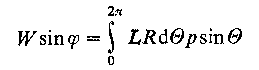
| (6.177)
|
gdzie: φ - kąt usytuowania linii działania obciążenia względem θ = 0, L-długość łożyska.
Całkując przez części uzyskuje się
| |
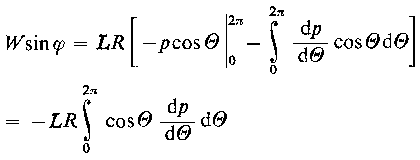
| (6.178)
|
korzystając z wyrażenia na (d p/d θ) w postaci równania (6.166), otrzymuje się
| |
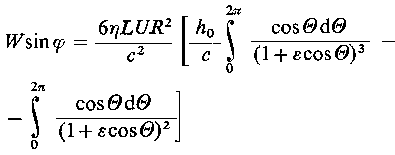
| (6.179)
|
Wyrażenie to można przedstawić w postaci sumy całek stosowanych do wyznaczenia rozkładu ciśnienia (d p.
Korzystając z tego, że
| |
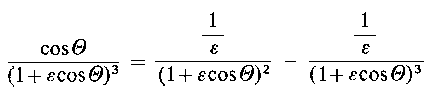
| (6.180)
|
oraz
| |
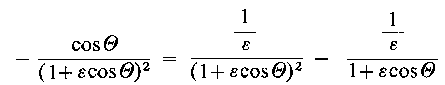
| (6.181)
|
równanie na (d W sin (d p (d φ) można sprowadzić do postaci
| |

| (6.182)
|
Jedyną nie wyznaczoną dotąd całką jest ostatnia całka, której wartość wynosi
| |
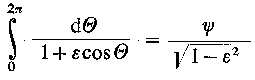
| (6.183)
|
Stosując transformację zmiennych, jak przy określaniu rozkładu ciśnienia, otrzymuje się
| |
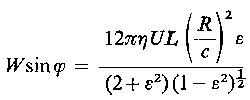
| (6.184)
|
Dla wyznaczenia kąta φ należy określić drugą składową obciążenia W, czyli Wcos φ
| |
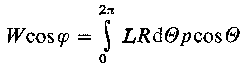
| (6.185)
|
Całkując przez części
| |
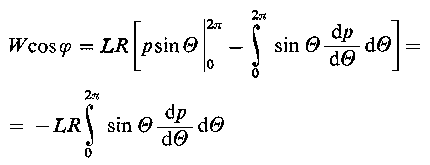
| (6.186)
|
oraz stosując podstawienie Sommerfelda, otrzymuje się
stąd zaś
a ponieważ W ≠ 0, więc f = ½π.
Wynika stąd, że W sin φ = W całkowitym obciążeniem. Ten nierzeczywisty wynik jest konsekwencją włączenia ciśnień ujemnych do przedziału całkowania, przy obliczaniu obciążalności.
Równanie (6.184) można przedstawić w postaci
|
S = |
η n
pśr |
( |
R
c |
)² = |
(2 + ε²)(1 - ε²)½
12 π² ε
| (6.188)
|
gdzie: S - liczba Sommerfelda, n - prędkość obrotowa wału w obr/s, pśr - średni nacisk jednostkowy w Pa.
Spotyka się też odmienne ujęcie liczby Sommerfelda
|
S0 = |
pśr
η n |
( |
c
R |
)² = |
1
2 π S
| (6.188a)
|
przy czym
|
pśr = |
W
L D |
= |
W
L 2R
| (6.189)
|
Liczba Sommerfelda jest bardzo wygodnym i pożytecznym parametrem bezwymiarowym, charakteryzującym pracę łożyska. Może być ona przedstawiona, jak widać z równania (6.188), jako funkcja jedynie jednego parametru geometrycznego - mimośrodowości względnej ε.
Naprężenia ścinające na powierzchni czopa są określone przez równanie (6.104). Po wprowadzeniu współrzędnych (R, θ) ma ono postać
|
τx = |
η U
h |
+ |
h
2R |
d p
d θ
| (6.189a)
|
Siła tarcia działająca na czop jest wyrażona równaniem
| |
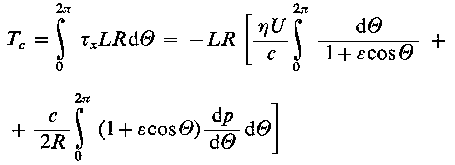
| (6.190)
|
Wykorzystując całki wyprowadzonych uprzednio wyrażeń uzyskuje się
|
Tc = η U L |
R
c |
4 π (1 + 2 ε²)
(2 + ε²)(1 + ε²)½
| (6.191)
|
Współczynnik tarcia można określić wzorem
|
µ = |
Tc
W |
= |
c
R |
1 + 2 ε²
3 ε
| (6.192)
|
Podobnie z równania (6.190) można określić zależność na siłę oporu tarcia na powierzchni panewki
|
Tp = η U L |
R
c |
4 π (1 - ε²)½
2 + ε²
| (6.193)
|
Różnica momentów czopa i panewki jest równoważona przez moment wytworzony przez siłę W na ramieniu R
|
R Tc = R Tp + W e
| (6.194)
|
Wyrażenie na siłę tarcia w łożysku z koncentrycznie obracającym się względem panewki czopem nazywa się równaniem Pietrowa. Otrzymuje się je wprost z równania (6.193) przez założenie ε = 0, z czego wynika oczywiście (d p/ d θ) = 0. Równanie Pietrowa ma następującą postać
|
Tc = 2 π η U L |
R
c
| (6.195)
|
Przedstawiona analiza ze względu na wiele założeń upraszczających daje niestety wyniki ilościowe, które daleko odbiegają od rzeczywistych warunków pracy łożyska. Błędne są one również jakościowo, ponieważ wartość ciśnienia ujemnego nie może być tego samego rzędu co dodatniego, oś wału zaś nigdy nie jest linią prostą.
Główne uproszczenia przedstawionej analizy można wyeliminować przez wprowadzenie bardziej realistycznych warunków brzegowych po stronie ujemnych ciśnień. Wykluczenie nieprawidłowości związanych z ujemnymi ciśnieniami uzyskuje się przy założeniu, że w punkcie, w którym ciśnienie spada do zera (punkt θ2 na rys. 6.54), gradient ciśnienia również osiągnie zero. Rozkład taki podano na rys. 6.55. Warunki brzegowe w tym przypadku, tzw. warunki brzegowe Reynoldsa, są następujące:
|
p |
= 0 |
dla |
θ = 0
| |
d p
d θ |
= 0 |
dla |
θ = θ2
| |
p |
= 0 |
dla |
θ = θ2
|
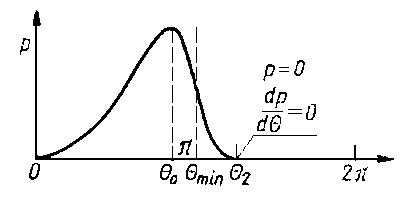 |
Rys. 6.55. Skorygowany rozkład ciśnienia w szczelinie wykluczający istnienie ciśnienia ujemnego (warunki brzegowe Reynoldsa)
|
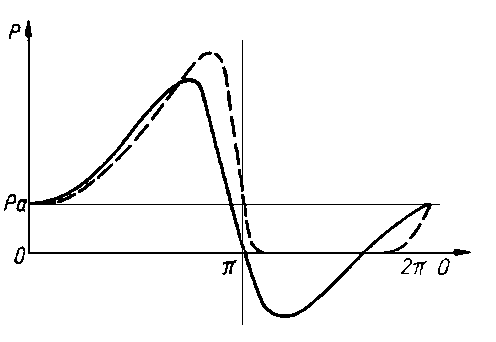 |
Rys. 6.56. Nośność łożyska ślizgowego dla warunków brzegowych Sommerfelda (linia ciągła) i Reynoldsa (linia przerywana)
|
Porównanie warunków brzegowych Sommerfelda i Reynoldsa przedstawiono na rys. 6.56. Ponieważ równanie (6.160) jest równaniem różniczkowym drugiego rzędu, dlatego też może ono uwzględnić jedynie dwa warunki brzegowe. Można jednak wykazać, że dwa ostatnie warunki brzegowe równania Reynoldsa stanowią szczególny przypadek bardziej ogólnego pojedynczego warunku.
Dwa ostatnie warunki brzegowe dla θ2 można przedstawić w postaci jednego warunku
Całkując równanie Reynoldsa uzyskuje się
| |
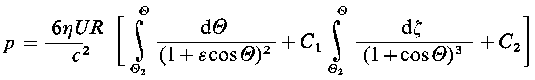
| (6.196)
|
Korzystając z podstawień
| |
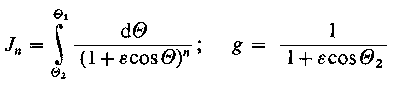
| (6.197)
|
można dla warunków brzegowych
|
p = |
0 |
dla |
θ1
| |
p = k |
d p
d θ |
dla |
θ2
|
wyznaczyć stałe całkowania C1 i C2,
|
C1 = - |
J2 + kg²
J3 + kg³ | |
C2 = k |
g² J3 - g³ J2
J3 + kg³
|
Wyrażenia na p oraz na (d p/ d θ) przyjmują teraz następującą postać
| |
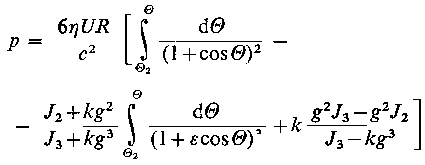
| (6.198a)
|
| |
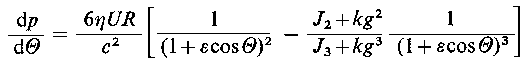
| (6.198b)
|
Ponieważ ε < l, Jn > 0 i g > 0, mianowniki wyrażeń nigdy nie znikają, dlatego warunki dla p = 0 i (d p/ d θ) = 0 przy θ = θ2 są następujące:
| dla |
p |
= 0 | |
k (g² J3 - g³ J2) = 0 | albo |
k g² (J3 - g J2) = 0
| (6.199a)
|
| dla |
d p
d θ |
= 0 | |
k g² (J2 + k g²) = J3 + k g³
| albo |
J3 - g J2 = 0
| (6.199b)
|
Wynika z tego, że aby p było równe 0 (p = 0 ) musi być spełniony warunek
lub też
| |
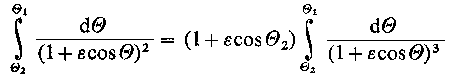
| (6.200b)
|
Warunek drugi (równość całek) wynika z przyrównania do zera drugiego czynnika warunku na p, tzn.
przy wykorzystaniu przytoczonych podstawień na In oraz g.
Z powyższych rozważań wynika, że gdy obowiązuje drugi warunek, tzn. równość całek, zarówno p jak (d p/ d θ) = 0 są równe zeru dla dowolnej wartości k, łącznie z k = 0, co odpowiada dwóm ostatnim warunkom (6.200).
Wykorzystując ponownie podstawienie Sommerfelda oraz korzystając z dwóch pierwszych warunków (6.199) można otrzymać rozkład ciśnienia p
| |
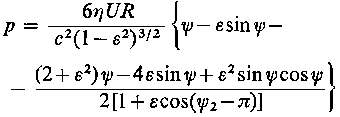
| (6.201)
|
przy czym
|
cos ψ = |
ε + cos θ
1 + cos θ
| (6.202)
|
gdzie ψ2 odpowiada θ2.
Stosując ostatni warunek (6.202) w postaci transformowanej na ψ, tzn. p = 0 przy ψ = ψ2 uzyskuje się równanie
|
ε[sin(ψ2 - p) cos(ψ - p) - ψ2] + 2[ψ2cos(ψ2 - p) - sin(ψ2 - p)] = 0
| (6.203)
|
Z wyrażenia tego można wyznaczyć ψ2, a zatem i θ2.
Równanie (6.203) wraz z określonym z równania (6.202) ψ2 określa rozkład ciśnienia spełniający warunki brzegowe Reynoldsa.
Analogicznie jak uprzednio można określić składowe obciążenia
| |
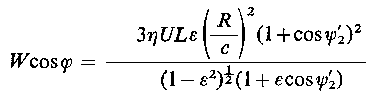
| (6.204a) |
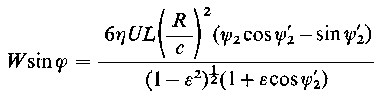
| (6.204b)
|
przy czym ψ'2 = ψ2 - π oraz całkowite obciążenie
| |
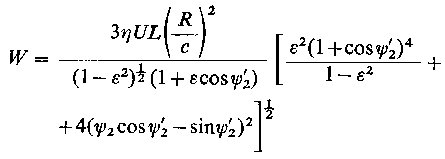
| (6.205)
|
a także
|
tg φ = - |
2 (1 - ε²)½(sin ψ'2 - ψ2 cos ψ'2)
ε(1 + cos ψ' 2)²
| (6.206)
|
Na tej podstawie można wyznaczyć
|
( |
R
c |
) | f = |
ε sin φ
2 |
+ |
2 π² S
1 - ε²
| (6.207)
|
Zastosowanie warunków Reynoldsa eliminuje obszar ujemnych ciśnień oraz pozwala przewidzieć usytuowanie osi wału (równanie (6.206)) zgodne z danymi doświadczalnymi. Wyniki obliczeń wykonanych na podstawie równań hydrodynamiki są podawane na ogół w postaci stabelaryzowanej.
6.6.2. Łożysko nieskończenie krótkie
Równanie (6.162) stosuje się, jak już wspomniano, do łożysk nieskończenie długich. Całkując to równanie otrzymuje się następujące wyrażenie
|
p = |
6 η U
h³ |
d h
d x |
z²
2 |
+ C1 z + C2
| (6.208)
|
Uwzględniając, że dla z = ±½L, p = 0 oraz wprowadzając współrzędne biegunowe, uzyskuje się
|
p(θ, z) = |
3 η U
R c² |
( |
L²
4 |
- z² |
) | ε sin θ
(1 + ε cos θ)³
| (6.209)
|
Rozkład ciśnienia jest paraboliczny. Jest to funkcja nieparzysta względem θ = π oraz p = 0. Oznacza to, że obszar występowania ciśnień ujemnych jest taki sam, jak obszar występowania ciśnień dodatnich.
Wykorzystując równanie (6.203) do obliczenia obciążalności łożyska można w pierwszym przybliżeniu ograniczyć całkowania do zakresu 0 ≤ θ ≤ π. Eliminuje to wpływ ciśnienia ujemnego. Wówczas odpowiednie składowe siły reakcji łożyska
| |
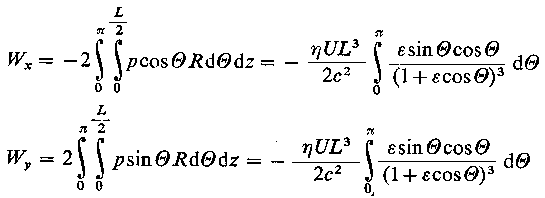
| (6.210)
|
Stosując podstawienie Sommerfelda i całkując otrzymuje się
|
Wx = |
η U L³
c² |
ε²
(1 - ε²)²
|
| |
Wy = |
η U L³
4 c² |
π ε
(1 - ε²)3/2
| (6.211)
|
Całkowita obciążalność wynosi
|
W = |
η U L³
4 c² |
ε
(1 - ε²)² |
[π² (1 - ε²) + 16 ε²]½
| (6.212)
|
Wyrażenie to można przedstawić następująco
|
η ω
p |
( |
L
c |
)² |
= S |
( |
L
D |
)² |
= |
(1 - ε²)²
π ε [π (1 - ε²) + 16 ε²]½
| (6.213)
|
Z równania (6.213) wynika, że żadne z występujących tam wyrażeń nie jest jawną funkcją średnicy łożyska D. Wpływ średnicy przejawia się jedynie poprzez zależność ε = ε(c), ponieważ wielkość c jest na ogół funkcją D. Oznacza to, że T(ε, D) = 0.
Z równań (6.211) można wyznaczyć kierunek działania wypadkowej siły reakcji W
|
tg φ = |
π
4 |
(1 - ε²)½
ε
| (6.214)
|
Ponieważ w rozważanym przypadku nie występują naprężenia ścinające spowodowane przepływem ciśnieniowym, więc naprężenie ścinające wyniesie
stąd zaś siła tarcia
| |
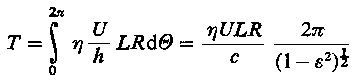
| (6.216)
|
Podobnie jak poprzednio, można wyznaczyć teraz współczynnik tarcia
|
µ = |
c
R |
2π² S
(1 - ε²)½
| (6.217)
|
Korzystając z równania (6.152) na jednostkowe natężenie przepływu q oraz z wyznaczonej zależności na p (6.208) można określić natężenie przepływu
| |
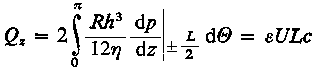
| (6.218)
|
Parametry charakteryzujące punkt, w którym występuje maksimum ciśnienia, można wyznaczyć z równań:
|
cos θ0 = |
1 - (1 + 24ε²)½
4 ε
| (6.219a)
|
|
h0 = |
c
4 |
[5 - (1 + 24ε²)½]
| (6.219b)
|
|
p0 = |
3 η U L
U R c² |
ε sin θ0
(1 + εcos θ'0)³
| (6.219c)
|
Przedstawiony model nieskończenie krótkiego łożyska stanowi dobre przybliżenie umożliwiające szacowanie charakterystyk krótkich łożysk poprzecznych pracujących z niewielką mimośrodowością. Dzięki swojej prostocie i zwartości matematycznego opisu jest on wygodny do analizy problemów hydrodynamicznego smarowania ślizgowych łożysk poprzecznych.
6.6.3. Łożysko z niepełną panwią
Z określenia łożysko z niepełną panwią wynika, że każde łożysko, którego panewka tworzy łuk o kącie środkowym mniejszym niż 2π jest zaliczane do tej grupy. W praktyce jednak łożyska takie mają najczęściej panewki o kącie mniejszym niż π. Analizę pracy łożyska z niepełną panwią można przeprowadzić na podstawie rys. 6.57.
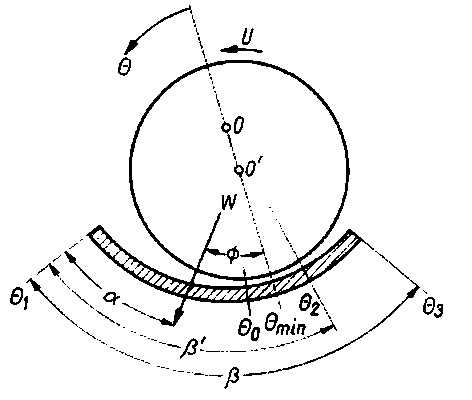 |
Rys. 6.57. Łożysko z niepełną panwią;
U - prędkość obwodowa,
b' - zmienna wartość kąta, przy której występuje dodatnia wartość ciśnienia oleju
|
Rozważania matematyczne są tu nieco bardziej skomplikowane niż poprzednio ze względu na istnienie dwóch dodatkowych zmiennych niezależnych: kąta przyłożenia obciążenia a oraz kąta łuku panewki b. Uproszczone rozwiązanie tego problemu oparte na schemacie zaproponowanym przez Sommerfelda jest podobne do przytoczonego uprzednio rozwiązania dla łożyska o pełnej panwi. Łożysko to zawiera także obszary podciśnienia. Na podstawie zależności (6.160) i następujących warunków brzegowych
|
p = |
p1 | |
dla |
θ = θ1
| |
p = |
d p
d θ |
= 0 |
dla |
θ = θ2
| |
p ≥ |
0 | |
dla |
θ1 < θ < θ2
| |
p = |
0 | |
dla |
θ > θ2
|
można uzyskać dla rozpatrywanego łożyska o niepełnej panwi rozwiązanie bardziej dokładne. Pomimo że metoda rozwiązania i uzyskane równania są podobne do rozważań przeprowadzonych dla łożyska o pełnej panwi, to jednak obliczenia towarzyszące tym operacjom są wyjątkowo żmudne i pracochłonne. Z tego też powodu wyniki są zazwyczaj podawane w formie graficznej.
Całkując równanie (6.160) przy zachowaniu nieokreślonych granic całkowania uzyskuje się
| |
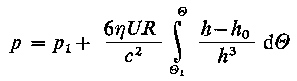
| (6.220)
|
Po zastosowaniu podstawień Sommerfelda oraz po ponownym całkowaniu otrzymuje się
| |
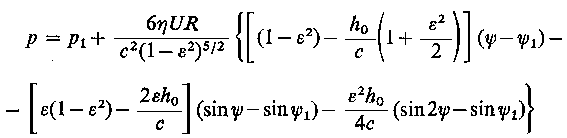
| (6.221)
|
gdzie ψ - pomocnicza zmienna w podstawieniu Sommerfelda, h0 - wartość wyznaczana z warunków granicznych dla θ2.
Wyniki całkowania równania (6.220) przedstawiono na rys. 6.58 oraz 6.59. Na rysunkach tych podano punkty reprezentujące maksymalną obciążalność łożyska. Cyfry umieszczone wzdłuż krzywych oznaczają odpowiednie wartości kąta θ. Przedstawiają one charakterystyki pracy łożysk z niepełną panwią w zależności od
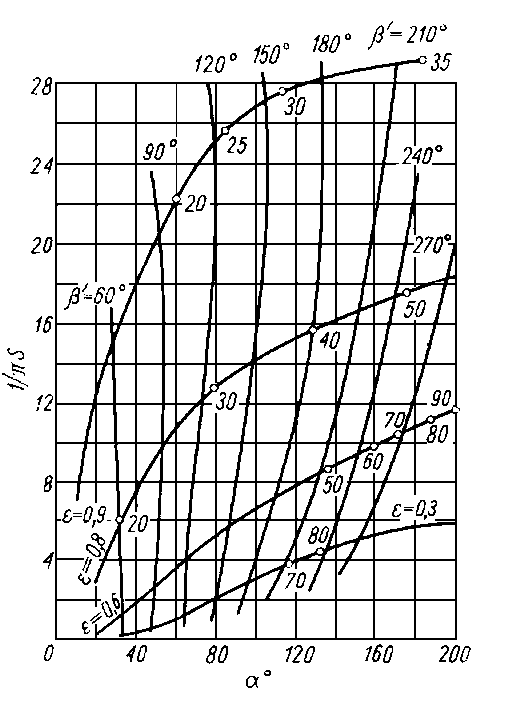 |
Rys. 6.58. Zależność obciążalności łożyska od kąta a przyłożenia obciążenia; S-linia Sommerfelda
|
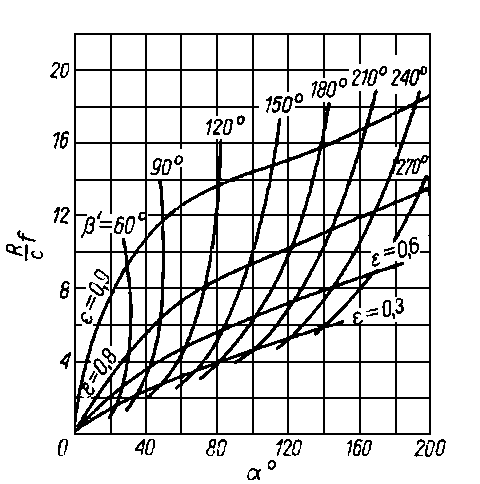 |
Rys. 6.59. Zależność względnej wartości współczynnika tarcia od kąta przyłożenia obciążenia a dla łożyska z niepełną panwią
|
kąta przyłożenia obciążeń a . Równania te wykluczają istnienie obszaru podciśnienia.
Ponieważ punkty na rys. 6.58 odpowiadają maksymalnej obciążalności, dlatego dla danego S i kąta łuku panewki b przy założeniu, że b = b ' można określić optymalny kąt przyłożenia obciążenia a . Jeżeli b > b ' to oczywiście obciążalność łożyska nie zmieni się, ponieważ w warunkach granicznych założono p = 0 dla θ > θ2. Wzrosną natomiast w takim przypadku opory tarcia o wartość wynikającą z łuku b - b ' ponieważ do ich występowania nie jest konieczne istnienie naprężeń normalnych p. Jeżeli b = 2a , wówczas łożysko jest obciążone symetrycznie.
Na rysunku 6.59 pokazano zależność względnego współczynnika tarcia (R/c) od kąta przyłożenia obciążenia. Parametrami krzywych są tu b oraz ε.
6.6.4. Łożysko ściśle pasowane
Łożysko, w którym średnice czopa i panewki są równe, nazywane jest łożyskiem ściśle pasowanym. Przykład takiego typu łożyska przedstawiono na rys. 6.60. Oczywiście w przypadku tym, jak wynika z definicji, nie występuje rozważany w każdym z po-
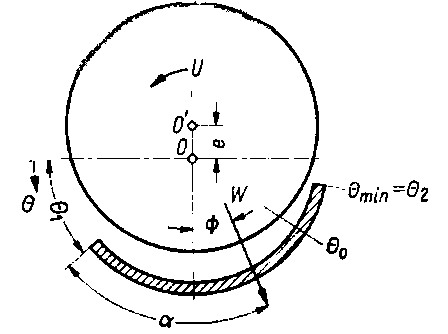 |
Rys. 6.60. Łożysko ściśle pasowane
|
przednich rodzajów łożysk luz promieniowy c; zatem c = 0. Wynika stąd, że równanie (6.163), przepisane dla tego przypadku, przyjmuje następującą postać
Obracając dla wygody całkowania 0 o 90° w kierunku obrotu czopa, w położenie podane na rys. 6.60a, otrzymuje się przekształcone wyrażenie na h
Korzystając z tej postaci oraz podstawiając do równania (6.166) h0 = sin θ0, otrzymuje się zależność na rozkład ciśnienia w łożysku ściśle pasowanym
| |
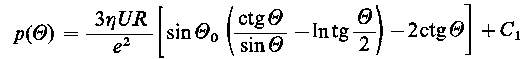
| (6.224)
|
Na podstawie warunków granicznych p(θ1 = p(θ2) = 0 można określić sin θ0 oraz C1, korzystając zaś ze znanych wyrażeń ogólnych można wyznaczyć obciążalność i siłę tarcia.
Charakterystyczne parametry trybologiczne opisujące pracę łożyska przy maksymalnym obciążeniu i minimalnej grubości warstwy oleju, są następujące:
- parametr obciążalności
- parametr oporu tarcia
- względny współczynnik tarcia
6.6.5. Łożysko z pływającym pierścieniem
Łożysko, do którego wprowadzono dodatkowo między czop a panewkę cienki, swobodnie poruszający się pierścień, nazywane jest łożyskiem z pływającym pierścieniem (rys. 6.61). Wprowadzenie pierścienia powoduje zmniejszenie strat ścinania w cieczy
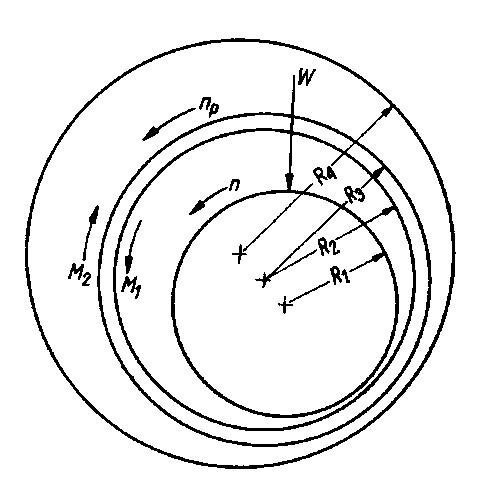 |
Rys. 6.61. Łożysko z pływającym pierścieniem;
n- prędkość obrotowa czopa,
np - prędkość obrotowa pierścienia
|
przez zmniejszenie względnych prędkości współpracujących powierzchni. Ponieważ straty te rosną z kwadratem prędkości, ale są tylko liniowo zależne od pola powierzchni, dlatego też zastosowanie pierścienia przy nie zmienionych pozostałych parametrach powoduje znaczne ich obniżenie.
Z rys. 6.61 wynika, że warunek równowagi dynamicznej dla pierścienia będzie spełniony wtedy, gdy suma obydwu momentów M1 i M2, działających ze strony cieszy na pierścień będzie równa zeru. Do obliczenia sił oporu tarcia Tc działających na zewnętrzną i wewnętrzną powierzchnię pierścienia, można wykorzystać równania służące do obliczenia tych wartości dla czopa.
Rozpatrywane łożysko można uważać za układ złożony z dwóch łożysk. Pierścień i czop tworzą przy tym założeniu jedno łożysko, zaś panewka i pierścień - drugie łożysko.
Siłę oporów tarcia można wyrazić zależnością
| |
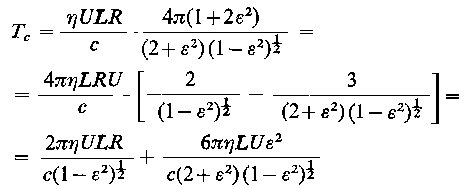
| (6.226)
|
Mnożąc licznik i mianownik drugiego członu przez (R/c)•(1/ε) oraz wykorzystując wyrażenie na W sin φ, uzyskuje się
|
Tc = |
2 πη U L R
c (1 - ε²)½ |
- |
ε c
2 R |
W sin φ
| (6.227)
|
Podobnie można obliczyć
|
Tc = |
2 πη U L R
c (1 - ε²)½ |
- |
ε c
2 R |
W sin φ
| (6.228)
|
Na tej podstawie można określić obydwa poszukiwane momenty
|
M1 = |
ε1c1
2 R |
W sin φ1 |
+ |
4 π²η L R2² (R1n - R2 n p)
c1 (1 - ε1²)½
| (6.229)
| |
M2 = |
ε1c2
2 R |
W sin φ1 |
+ |
4 π²η L R33 n p
c1 (1 - ε2²)½
|
gdzie: ε - mimośrodowość względna czopa i pierścienia, ε2 - mimośrodowość względna pierścienia i panewki. c1 - luz promieniowy między czopem a pierścieniem, c2 - luz promieniowy między pierścieniem a panewką, φ1 - kąt usytuowania linii działania obciążenia w wewnętrznej przestrzeni pierścienia, φ2 - kąt usytuowania linii działania obciążenia w zewnętrznej przestrzeni pierścienia, n - prędkość obrotowa czopa, np - prędkość obrotowa pierścienia, pozostałe oznaczenia wg rysunku.
Łożysko, którego czop i panewka obracają się w jednym kierunku, można zastąpić równoważnym łożyskiem, w którym czop obraca się z prędkością równą sumie prędkości rzeczywistego czopa i panewki. Pamiętając o tym można dla każdego z wydzielonych abstrakcyjnie dwóch łożysk napisać równanie na liczbę Sommerfelda
| |
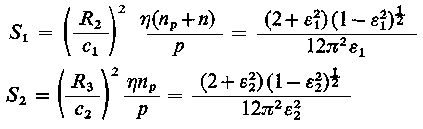
| (6.230)
|
Na podstawie przytoczonych równań można wyznaczyć całkowite straty mocy H w łożysku z pływającym pierścieniem
| |
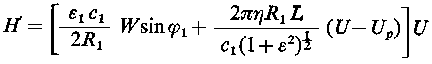
| (6.231)
|
gdzie: U - prędkość obwodowa czopa. Up - prędkość obwodowa panewki.
Na rys. 6.62 przedstawiono zaleźność stosunku prędkości obrotowej pierścienia i czopa od stosunku luzów występujących w łożysku z pływającym pierścieniem.
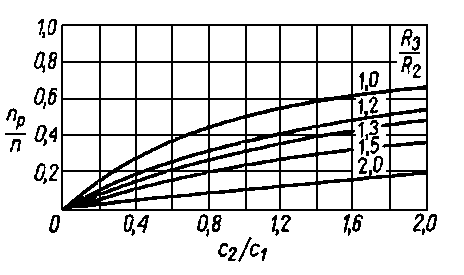 |
Rys. 6.62. Zależność poślizgu pierścienia względem czopa np/n od stosunku luzów promieniowych C2/C1 w łożysku z pływającym pierścieniem
|
Porównania dwóch równoważnych łożysk ślizgowych: łożyska tradycyjnego (bez pierścienia) i łożyska z pierścieniem pływającym można dokonać przy założeniu
Indeks t oznacza łożysko tradycyjne, zaś brak indeksu - łożysko z pływającym pierścieniem.
Przyjmując za kryterium porównania łożysk grubość warstwy oleju powstającej na zewnątrz pierścienia, które jest warunkiem bardziej rygorystycznym niż grubość warstwy wewnątrz pierścienia, można stwierdzić, że przy (St/Sp) > 1 ??? sprawdź, chyba błąd łożysko z pływającym pierścieniem ma mniejszą obciążalność, a przy (St/Sp > 1 - większą obciążalność. Straty mocy są w obydwu przypadkach mniejsze niż w łożysku tradycyjnym.
6.6.6. Łożysko porowate
Łożysko z panewką wykonaną z materiału porowatego jest nazywane łożyskiem porowatym. W panewce takiej olej wypływa z jej powierzchni z pewną prędkością v0. Jeżeli przez qy oznaczyć natężenie przepływu przypadające na jednostkę powierzchni, wówczas
|
qy = - |
∂ p
∂ y |
│
│
│ |
y = 0 |
Φ
η
| (6.232)
|
gdzie: (∂ p/∂ g ) gradient ciśnienia na powierzchni panewki, Φ tzw. przepuszczalność, czyli właściwość materiału panewki zależna od porowatości i rozmiarów porów w m².
Warunek ciągłości przepływu dla panewki ma następującą postać
|
Ń p = |
Φ
η |
Ń² p = 0
| (6.233)
|
gdzie: - Ń operator Hamiltona : (∂/∂ x) + (∂/∂ y) + (∂/∂ z), Ń² - operator Laplace'a : (∂²/∂ x²) + (∂²/∂ y²) + (∂²/∂ z²)
Ponieważ - (Φ/η ≠ 0, więc Ń² p = 0.
Oprócz warunku Ń² p = 0 musi być słuszne także w takim przypadku
równanie Reynoldsa. Dlatego też zagadnienie sprowadza się do rozwiązania układu dwóch równań różniczkowych. Kładąc w równaniu Reynoldsa wyznaczone wyrażenie na V0 uzyskuje się
| |
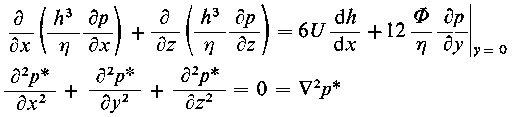
| (6.234a)
| | (6.234b)
|
Układ ten można rozwiązać przy następujących założeniach:
1) łożysko jest nieskończenie krótkie,
2) gradient (∂/∂ y) jest liniowy w całej grubości warstwy porowatej i przyjmuje wartość równą 0 na wewnętrznej powierzchni warstwy porowatej.
Z założenia 1 wynika, że (∂²/∂ x²) = 0, zaś z założenia 2 wynika (∂²/∂ y²) = const = K.
Po uwzględnieniu tych założeń równanie Laplace'a daje
natomiast po scałkowaniu wyrażenia
| |
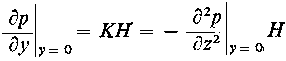
| (6.236)
|
gdzie H - grubość warstwy porowatej.
Podstawiając wyznaczone wyrażenia do równania (6.234) i uwzględniając przy tym, że (∂/∂ x) [(h³/η ) (∂ p/∂ x) = 0 uzyskuje się
|
(h³ + 12 Φ H) |
∂² p
∂ z² |
= 6 U η |
∂ h
∂ x
| (6.237)
|
Stąd wynika
| |
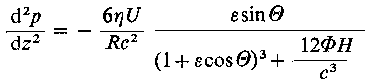
| (6.238)
|
Równanie to po scałkowaniu, dla θ = π, ma postać
| |
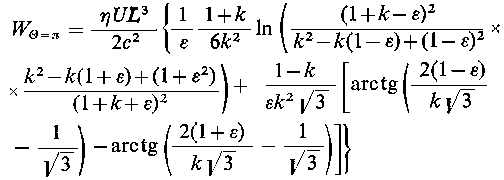
| (6.239)
|
gdzie k³ = 12 (Φ H/c³)
Na rys. 6.63 przedstawiono porównanie obciążalności łożyska porowatego, obliczonej wg równania (6.222), z obciążalnością tradycyjnego nieskończenie krótkiego łożyska poprzecznego, obliczoną wg równania (6.212).
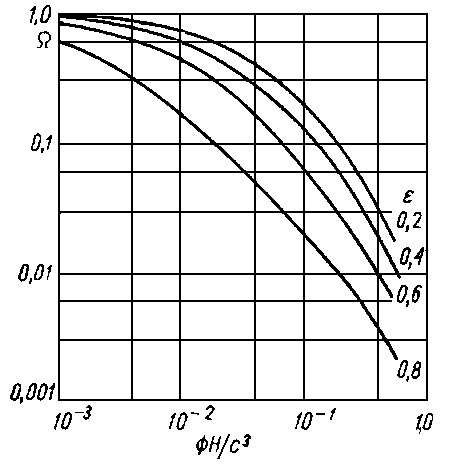 |
Rys. 6.63. Porównanie obciążalności łożyska porowatego i klasycznego;
- e = e/c,
- F H/c³ -parametr konstrukcji (bezwymiarowy),
- c - luz promieniowy w m,
- F - przepuszczalność w m²,
- H - grubość warstwy porowatej w m,
- W - stosunek obciążalności łożyska porowatego i tradycyjnego
|
Na osi rzędnych odłożono stosunek tych zależności
|
W = |
obciążalność łożyska porowatego
obciążalność łożyska tradycyjnego
|
|
Analogicznie jak poprzednio można wyznaczyć względny współczynnik tarcia
|
R
c |
f = |
2 π² S
Ω |
1
(1 - ε)½ |
+ |
ε
2 |
sin φ
| (6.240)
|
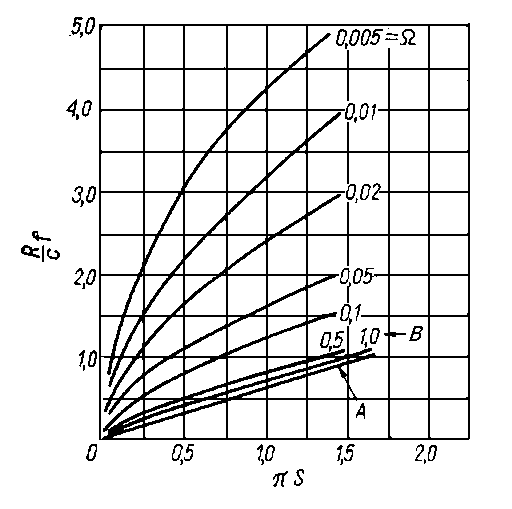 |
Rys. 6.64. Zależność względnego wspólczynnika tarcia od liczby Sommerfelda;
- A - krzywa dla klasycznego łożyska współśrodkowego (równanie Pietrowa),
- B - krzywa dla klasycznego łożyska niewspółśrodkowego
|
Na rys. 6.64 przedstawiono wartość względnego współczynnika tarcia dla różnych wartości Ω
. Krzywa o wartości Ω = l odpowiada, zgodnie z definicją Ω, łożysku klasycznemu. Dla porównania umieszczono tam także krzywą A opracowaną na podstawie równania Pietrowa, a więc słuszną dla łożyska współśrodkowego.
6.6.7. Łożyska wzdłużne jednowymiarowe
Analiza łożysk wzdłużnych jest nieco łatwiejsza niż analogiczna analiza łożysk poprzecznych. Wyrażenia na grubość warstwy cieczy są tu o wiele prostsze. Warunki brzegowe są także w tym przypadku mniej skomplikowane, nie występuje też problem ciśnienia ujemnego. Ciśnienia na wejściu i wyjściu mają zazwyczaj wartość ciśnienia atmosferycznego.
Rayleigh uzyskał kilka rozwiązań dla łożyska wzdłużnego jednowymiarowego, a także wyprowadził wyrażenia określające optymalny kształt warstewki cieczy i wymiary łożyska. Wyniki te odbiegają od rzeczywistości, jednakże i w tym przypadku wiele parametrów bezwymiarowych oraz wniosków jakościowych wysnutych z analizy jednowymiarowego łożyska obowiązują również dla rozwiązań dokładniejszych.
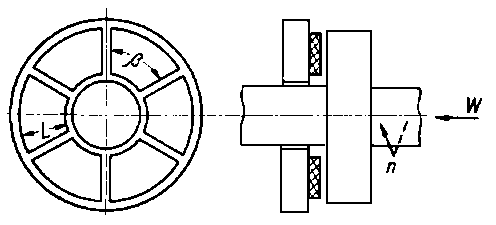 |
Rys. 6.65. Schemat łożyska wzdłużnego
|
Typowy przykład łożyska wzdłużnego przedstawiono na rys. 6.65. Segmenty, z których składa się takie łożysko, mogą mieć różne kształty. Stosując klasyczny układ współrzędnych otrzyma się
|
d p
d x |
-6 η U = |
h - h0
h³
| (6.241)
|
Znak minus oznacza, że wektor prędkości U ma zwrot przeciwny do x.
Po scałkowaniu otrzymuje się
| |
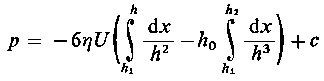
| (6.242)
|
przy czym
|
p( h1) = p( h2) = 0
| (6.243)
|
Całkując przez części wyrażenie na obciążalność uzyskuje się
| lub |
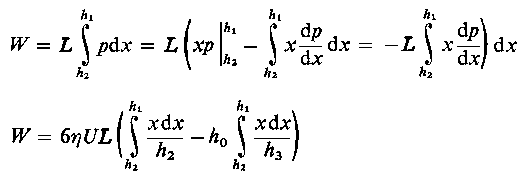
| (6.244a)
| | (6.244b)
|
Korzystając z twierdzenia o średniej całkowej można wyznaczyć wartość x, która dzieli rozkład ciśnienia na dwie części o równych sobie polach pod krzywą p
| |
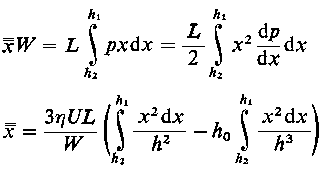
| (6.245)
|
Wyrażenie na naprężenia ścinające wynika z równania (6.215)
|
τ = |
η U
h |
+ |
h
2 |
d p
d x
| (6.246)
|
Stosując zaś zależność na (d p/d x) otrzymuje się naprężenia ścinające
|
τ = η U |
4 h - 3 h0
h²
| (6.246)
|
oraz silę tarcia
| |
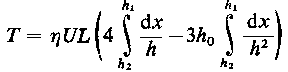
| (6.247)
|
Przytoczone wyżej równania mogą zostać wykorzystane do analizy łożysk o różnych kształtach warstwy oleju.
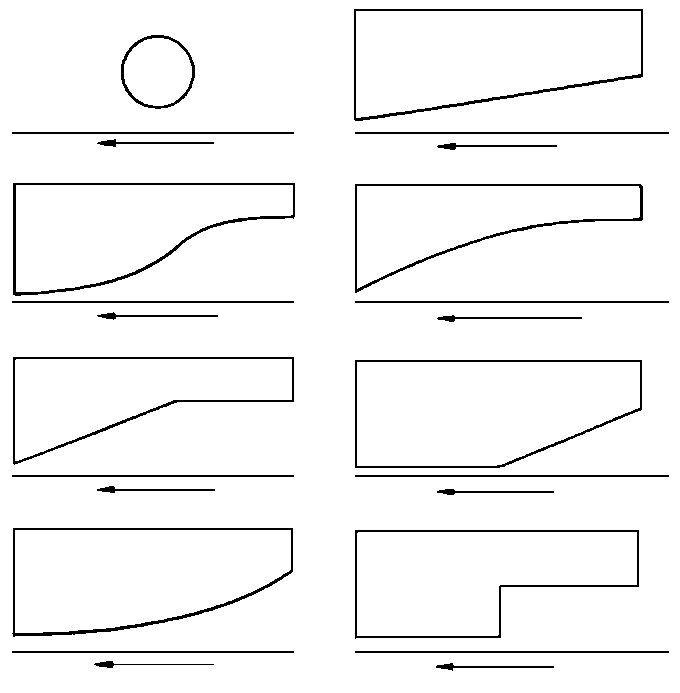 |
Rys. 6.66. Modele geometryczne do analizy smarowania hydrodynamicznego
|
Na rys. 6.66 przedstawiono przykłady podstawowych kształtów geometrycznych łożysk, dla których przeprowadzono analizę wg przytoczonej zasady.
Łożysko z płaskim i ściętym ślizgaczem Grubość warstwy cieczy dana jest równaniem
|
h = α x = |
h2(a - 1)
B |
x
| (6.248)
|
przy czym a = h1/h2
gdzie: h1, h2 - grubość warstwy oleju w punkcie początkowym i końcowym klina smarnego.
Całkując równanie (6.241) w granicach od x1 = h1/a do x2 = h2/a uzyskuje się wyrażenie na rozkład ciścienia p
| |
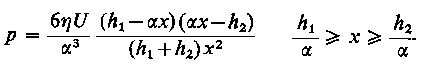
| (6.249)
|
skąd
|
h0 = |
2 h1h2
h1 + h2 |
= |
2 a
1 + a |
h2
| (6.250)
|
Z równań (6.244) do (6.248) można wyznaczyć
|
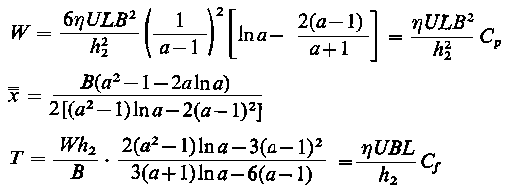
| (6.251a)
| | (6.251b)
| | (6.251c)
|
Wartości bezwymiarowych współczynników Cp oraz funkcji s przedstawiono na rys. 6.67.
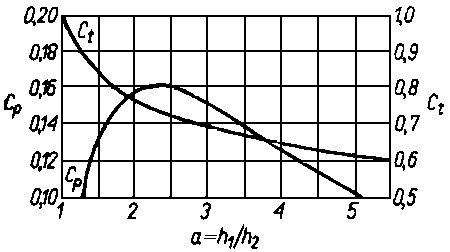 |
Rys. 6.67. Wartości bezwymiarowych współczynników charakteryzujących zmianę obciążalności Cp oraz siły tarcia Cf dla łożyska ze ściętym płaskim ślizgiem
|
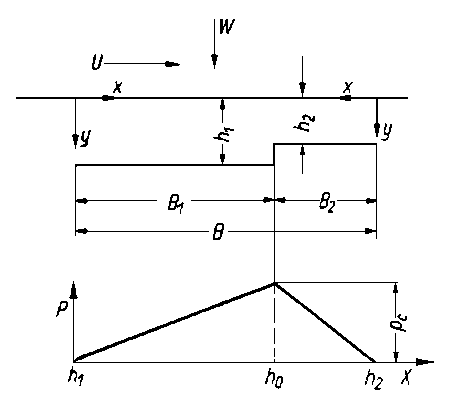 |
Rys. 6.68. Model łożyska Rayleigha
|
Łożysko Rayleigha. Na rys. 6.68 przedstawiono przykład płaszczyzny przemieszczającej się względem płytki z występem. Konfiguracja ta tworzy tzw. łożysko Rayleigha. Jeżeli w równaniu (6.248) podstawić h = const i założyć warunki izotermiczne, wówczas ciśnienie przewidywane przez teorię hydrodynamiczną będzie równe zeru. Oznacza to, że łożysko o stałej grubości warstwy cieczy nie ma żadnej obciążalności. Jednakże w przypadku, gdy w płytce istnieje wycięcie (rys. 6.69), wówczas w łożysku powstają siły hydrodynamiczne.
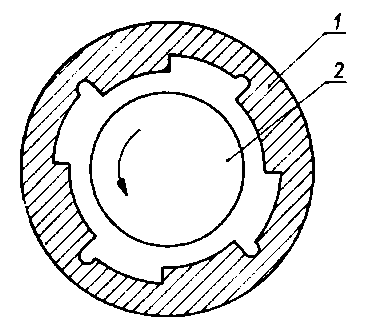 |
Rys. 6.69. Model łożyska Rayleigha z poprzecznymi występami;
- 1 - łożysko,
- 2 - wał
|
Odpowiednie wyrażenia opisujące grubość warstwy cieczy mają wtedy następującą postać: h = h 1 w obszarze B1, h = h2 w obszarze B2, (rys. 6.68).
Całkując równanie (6.242) przy założeniu h = const uzyskuje się
|
P = 6 η U |
n0 - h
h³ |
x + C
| (6.252)
|
Podstawiając p = 0 dla x = 0 oraz p = pc dla x = B1, gdzie pc jest ciśnieniem w miejscu istnienia występu, otrzymuje się
|
C1 = 0 |
oraz |
pc = 6 η U |
h1 - h0
h1³ |
B1
| (6.253)
|
Podobnie dla obszaru B2
|
C1 = 0 |
oraz |
pc = 6 η U |
h0 - h2
h2³ |
B2
| (6.254)
|
Ponieważ wartości pc są takie same w punkcie x = B1 dla obydwu obszarów, można więc je przyrównać
|
h1 - h0
h1³ |
B1 |
= |
h0 - h2
h2³ |
B2
| (6.255)
|
skąd można wyznaczyć
|
h0 = |
h1 h2(B1 h2² + B2 h1²)
B1 h2³+ B2 h1³
| (6.256)
|
Dla obszaru B1 rozkład ciśnienia jest zatem następujący
|
p( x ) = |
6 η U
h1² |
[ |
1 - |
h2(B1 h2² + B2 h1²)
B1 h2³+ B2 h1³ |
] |
x
| (6.257a)
|
dla obszaru B2
|
p( x ) = |
6 η U
h2² |
[ |
h1(B1 h2² + B2 h1²)
B1 h2³+ B2 h1³ |
- 1 |
] |
x
| (6.257b)
|
Oczywiście dla h 1 = h 2, lub B 1 = 0 albo też B 2 = 0 ciśnienie przyjmuje wartość p = 0.
Obciążalność rozważanego łożyska jest określona zależnością
| |
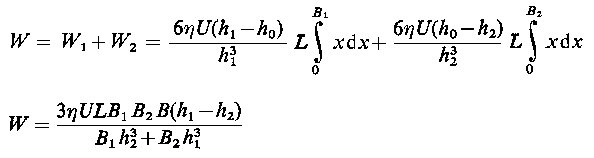
| (6.258)
|
Rayleigh badając omawiany zarys doszedł do wniosku, że stwarza on optymalne warunki do powstawania warstwy smaru o maksymalnej obciążalności. Wniosek ten wykorzystano do skonstruowania łożyska poprzecznego z występami zwanymi od nazwiska wynalazcy - progami Rayleigha (rys. 6.69). Kształt ślizgacza z występem jest także optymalny.
Łożysko z wahliwą płytką. W odróżnieniu od elementów łożysk wzdłużnych przemieszczających się ruchem postępowym przedstawione na rys. 6.70
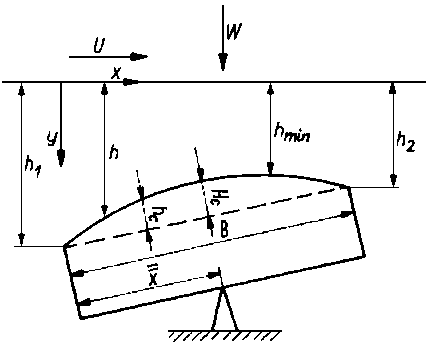 |
Rys. 6.70. Łożysko z wahliwą płytką
|
łożysko składa się z płaszczyzny przemieszczającej się względem przegubowo zamocowanej płytki. Zamocowanie takie umożliwia zgodnie z zasadą Le Chateliera-Brauna optymalne ustawienie położenia płytki tak, aby obciążalność była w danych warunkach maksymalna. Wprowadzone dla łożyska ze ściętym płaskim ślizgaczem zależności znajdują zastosowanie także i w tym przypadku. Ponieważ płytka jest podparta przegubowo, siła jest przenoszona przez punkt podparcia. Wynika stąd, że dla uzyskania swobodnego położenia płytki, punkt ten powinien być położony w odległości x obliczonej z równania (6.251b)
| |
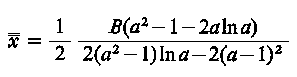
| (6.259)
|
Wartość x jest oczywiście ściśle związana z wartościami h1 i h2. Dla danego położenia płytki należy obliczyć wartość W ustalić zależność W = f(a , x ). Funkcja ta jest zwykle podawana w formie graficznej.
Omówione wyżej zjawiska znalazły zastosowanie w łożyskach poprzecznych z wahliwymi płytkami panwiowymi. Schemat rozwiązania konstrukcyjnego takiego łożyska przedstawiono na rys. 6.71.
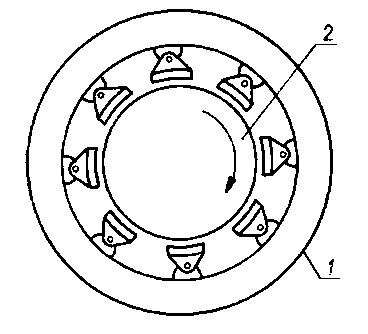 |
Rys. 6.71. Łożysko poprzeczne z wahliwymi płytkami;
- 1 - stała obudowa,
- 2 - wał
|
6.7. Smarowanie hydrostatyczne
Smarowanie hydrostatyczne jest to rodzaj smarowania polegający na tworzeniu między współpracującymi powierzchniami warstwy cieczy, w której występuje statyczne ciśnienie, powstające na skutek ciągłej cyrkulacji cieczy podtrzymywanej przez źródło ciśnienia, równoważące zewnętrzne obciążenie przy całkowitym oddzieleniu od siebie współpracujących powierzchni.
6.7.1. Zasada smarowania hydrostatycznego
Ideę smarowania hydrostatycznego zademonstrowano po raz pierwszy na Paryskiej Wystawie Przemysłowej w 1878 r. Wystawiono tam pozornie bezużyteczny eksponat o nazwie „Le Chemin de fer de glace” (kolej na lodzie). Była to bryła metalu wsparta na czterech podporach, zakończonych płaskimi, lekkimi, wklęsłymi stopami. Stopy te spoczywały na gładkim metalowym podłożu. Przez otwory w podporach tłoczony był olej, który wypływał pod stopami tak, że cała bryła unosiła się lekko i pływała na utworzonej w ten sposób warstwie cieszy. Opory tarcia między stopami a podłożem były bardzo małe w porównaniu z oporami tarcia suchego. Ciężka bryła metalu przesuwała się z dużą łatwością.
Opisany pierwowzór łożyska ślizgowego smarowanego hydrostatycznie dał początek serii prac, które doprowadziły do sformułowania zasad jego zastosowania we współczesnych urządzeniach i maszynach. Zjawisko smarowania hydrostatycznego jest wykorzystywane obecnie w najróżnorodniejszych rozwiązaniach konstrukcyjnych dzięki temu, że:
- grubość warstwy smarującej zależy w niewielkim stopniu od obciążenia,
- obciążalność łożyska zależy w niewielkim stopniu od prędkości względnej trących powierzchni,
- opory tarcia są znikomo małe.
Smarowanie to zapewnia dużą dowolność w wyborze rozwiązania konstrukcyjnego. Jego unikalną zaletą jest to, że opory tarcia są bardzo małe także przy rozruchu nieruchomych współpracujących elementów urządzeń. Na rys. 6.72 przedstawiono schematycznie przykłady wykorzystania smarowania hydrostatycznego do łożyskowania elementów obciążonych siłami o kierunku osiowym (rys. 6.72a), promieniowym (rys. 6.72b) oraz ukośnym rys. 72c).
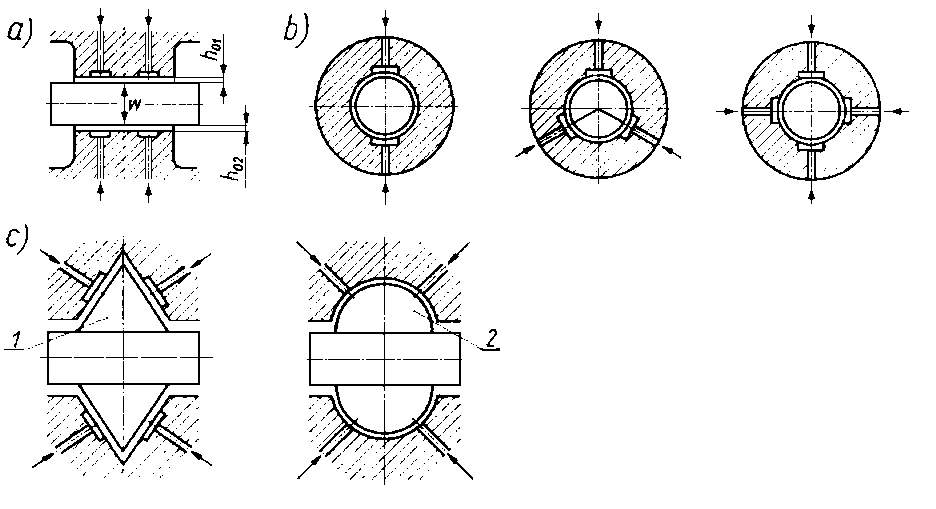 |
Rys. 6.72. Modele smarowania hydrostatycznego łożysk obciążonych sitami w kierunku:
- osiowym,
- pionowym,
- ukośnym;
- -stożek,
- - czasza kulista
|
Zasada smarowania hydrostatycznego znalazła powszechne zastosowanie w łożyskowaniu wielu elementów maszyn. Wykorzystuje się ją między innymi w następujących przypadkach:
- w łożyskach wzdłużnych (rys. 6.73),
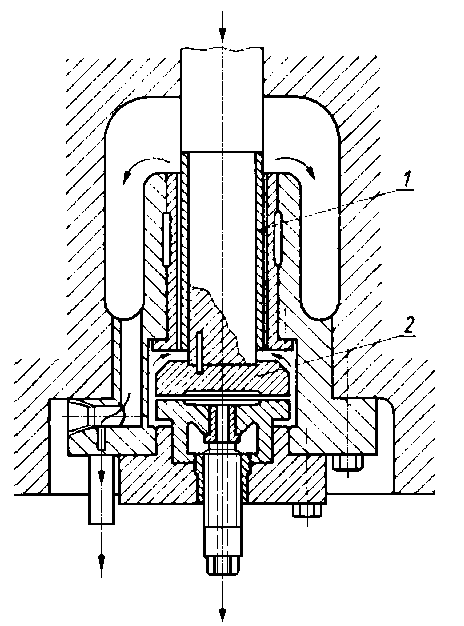 |
Rys. 6.73. Smarowanie hydrostatyczne łożyska stopowego;
- - tuleja prowadząca,
- - łożysko stopowe
|
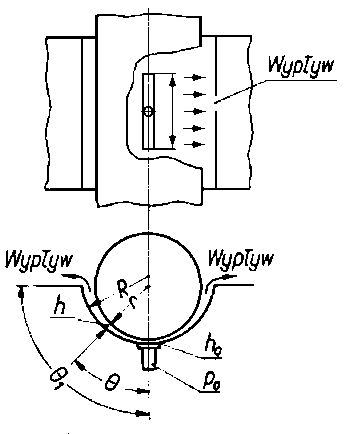 |
Rys. 6.74. Schemat zastosowanej poduszki hydrostatycznej do podnoszenia wału
|
- do podnoszenia wałów ciężkich maszyn wirnikowych, w celu zmniejszenia tarcia przy ich rozruchu (rys. 6.74),
- w łożyskach ślizgowych poprzecznych, gdy prędkość obrotowa wału jest za mała do wytworzenia dostatecznej warstwy cieczy,
- w prowadnicach, w celu zmniejszenia tarcia elementów poruszających się ruchem prostoliniowym (rys. 6.75),
- w urządzeniach do badania łożysk ślizgowych, w celu zredukowania oporów tarcia powierzchni podpierających (rys. 6.76),
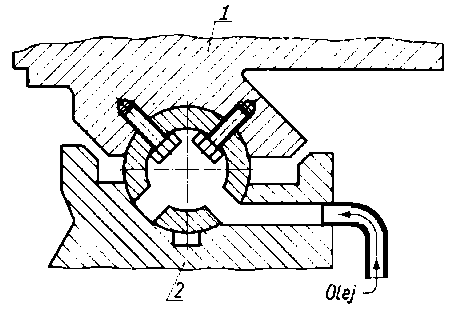 |
Rys. 6.75. Hydrostatyczne smarowanie prowadnic frezarki;
- - stół,
- - łoże
|
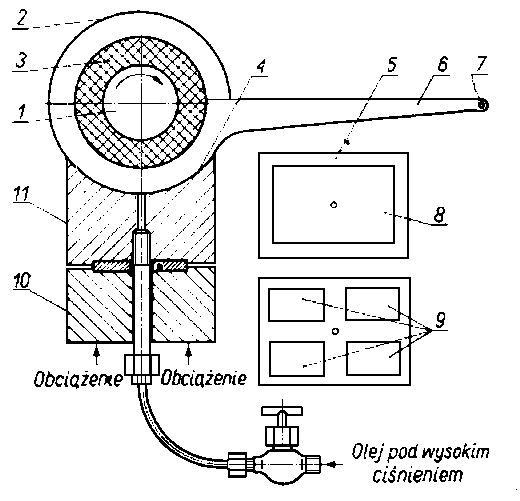 |
Rys. 6.76. Smarowanie hydrostatyczne w urządzeniu do badania łożysk ślizgowych;
- - wał,
- - uchwyt,
- - łożysko,
- - obie powierzchnie nakrywają się,
- - warianty płytek panwiowych,
- - ramię,
- - waga,
- - wgłębienia,
- - wgłębienia,
- - klocek dociskowy,
- - płytka panwiowa
|
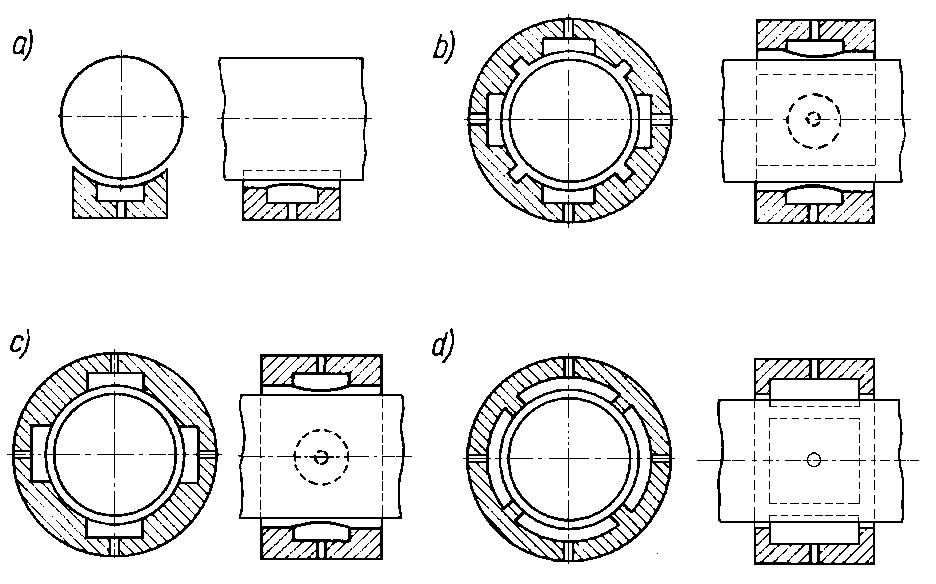 | |
Rys. 6.77. Schematy poprzecznego łożyska ślizgowego smarowanego hydrostatycznie
|
- w celu zamortyzowania ruchów współpracujących ze sobą wszelkiego rodzaju płyt, oddzielonych lepką cieczą,
w celu utrzymania zadanego luzu między powierzchniami.
We wszystkich wymienionych przykładach warstwa cieczy, która oddziela współpracujące elementy maszyn czy urządzeń utrzymywana jest w wyniku ciągłego doprowadzania smaru z zewnątrz pod pewnym ciśnieniem. Na rys. 6.77 przedstawiono schemat działania typowego poprzecznego łożyska ślizgowego smarowanego hydrostatycznie.
Ciecz doprowadzana w obszar tarcia przez otwory wlotowe Rw (rys. 6.78) pod ciśnieniem pompy pz wypływa przez szczeliny R1, R2. Szczeliny te istnieją
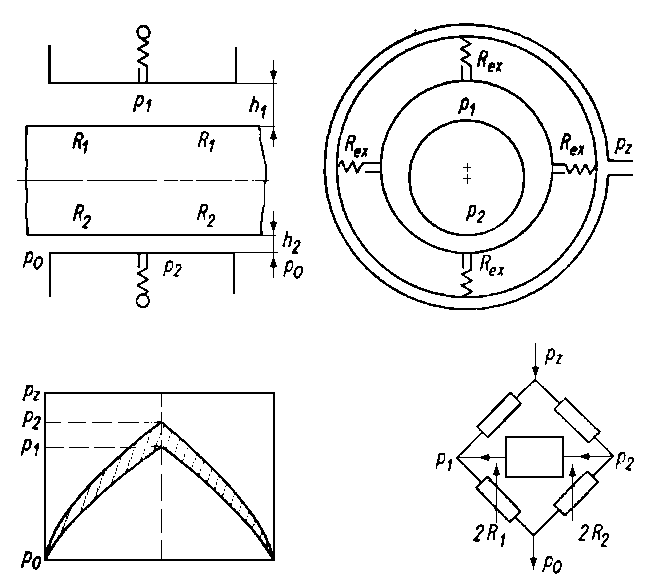 |
Rys. 6.78. Analog elektryczny poprzecznego łożyska ślizgowego smarowanego hydrostatycznie przedstawiający zależność obciążenia od średnicy czopa i wartości ciśnienia na wlocie do łożyska; Rex - regulowane wartości oporów
|
między powierzchniami czopa i panewki. Ciśnienie cieczy może być regulowane na zewnątrz lub też kompensowane wewnątrz łożyska. W przypadku współśrodkowego ustawienia czopa i panewki, tzn. gdy luzy h1= h2, ciśnienia p1 i p2. odpowiednio w górnej i dolnej części łożyska są równe. Na czop nie działa siła wypadkowa (jeśli pominąć ciężar wału). Jeżeli na skutek działania obciążenia zewnętrznego wał zostanie wytrącony z położenia równowagi, to zwiększy się luz h1 i zmniejszy się luz h2. Zmiana taka spowoduje zmianę wymiarów szczelin wypływowych R1, R2 Nastąpi wzrost oporów przepływu w części dolnej i spadek oporów przepływu w części górnej łożyska. Ponieważ zmiana oporów przepływu wpływa na wartość ciśnienia, dlatego też wzrośnie ciśnienie p2 i zmniejszy się ciśnienie p1. Wielkość powstającej w ten sposób siły wypadkowej, przeciwdziałającej wychyleniu wału, jest proporcjonalna do pola zakreskowanego obszaru na wykresie ciśnień.
W łożysku hydrostatycznym straty tarcia są znikomo małe. Istnieją rozwiązania konstrukcyjne, które charakteryzują się małymi współczynnikami tarcia. I tak np. hydrostatyczne smarowanie słynnego, o masie 450 t teleskopu na górze Mount Palomor umożliwiło zredukowanie współczynnika tarcia do wartości 0,000004. Jednakże całkowita moc potrzebna do zapewnienia pracy układów smarowania hydrostatycznego jest stosunkowo duża. Wynika to z konieczności utrzymania odpowiedniego ciśnienia cieczy. Dlatego też prawidłowo zaprojektowany układ smarowania wymaga optymalizacji zasilania i obciążalności. Na rys. 6.79 przedstawiono przykłady zależności strat mocy od grubości warstwy cieczy dla łożyska turbo-prądnicy.
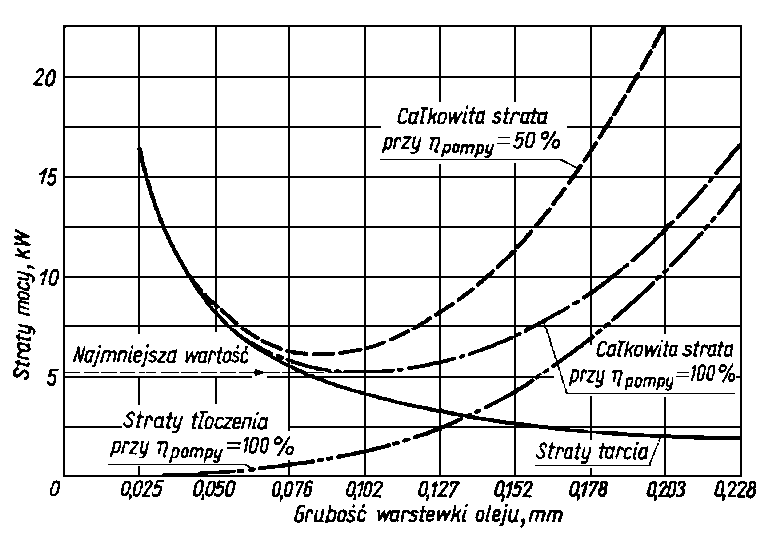 | |
Rys. 6.79. Zależność strat tarcia i tłoczenia cieczy w łożysku stopowym
|
Z rysunku wynika, że zmniejszenie strat tarcia odbywa się wskutek wzrostu strat tłoczenia.
6.7.2. Łożysko ślizgowe poprzeczne
Rozkład ciśnienia w hydrostatycznym łożysku poprzecznym można wyznaczyć z równania Reynoldsa. W przypadku nieruchomego czopa, tzn. gdy V = 0, równanie (6.94) przyjmie następującą postać
|
∂
∂ x |
( |
h³ |
∂ p
∂ x |
) |
+ |
∂
∂ z |
( |
h³ |
∂ p
∂ z |
) |
= 0
| (6.260)
|
lub też, uwzględniając h = h( x ), otrzyma się
|
∂² p
∂ z² |
+ |
∂² p
∂ x² |
+ |
3
h |
∂ h
∂ x |
∂ p
∂ x |
= 0
| (6.261)
|
Podstawiająca h = c(1 - cos θ ) uzyskuje się
Warunki brzegowe są następujące:
|
p = | p0 |
dla |
z = ±½ L
| |
p = | pw( x ) |
dla |
z = 0
|
gdzie: p0 - ciśnienie otoczenia w Pa, pw - ciśnienie cieczy na wlocie do łożyska w Pa.
Natężenie przepływu przypadające na jednostkę długości obwodu można wyznaczyć z równania
|
qw = 2 |
[ |
- |
h³
12 η |
( |
∂ p
∂ z |
) |
w |
]
| (6.263)
|
Jeżeli ciecz jest dostarczana do łożyska przez przewody zasilające, w których przepływ jest laminarny, to spadek ciśnienia w przewodzie jest następujący
|
pz - pw = |
8 η Q L
π a4
| (6.264)
|
gdzie: pz -ciśnienie zasilania w Pa, L - długość przewodu zasilającego w m, a - średnica przewodu zasilającego w m.
Jeżeli oznaczy się przez N liczbę przewodów zasilających, to liczba doprowadzeń przypadających na jednostkę długości obwodu wynosi n = [N/(2 π R)]. Równanie (6.263) przyjmie przy tych założeniach postać
|
qw= |
π a4 n
8 η L |
( pz - pw )
| (6.265)
|
Stosując warunek ciągłości strugi na wejściu do łożyska, uzyskuje się
|
qw= |
π a4 n
8 η L |
( pz - pw ) |
= |
h³
6 η |
( |
∂ p
∂ z |
) |
w
| (6.266)
|
Podstawiając do równania (6.266) wyrażenie na grubość warstwy cieczy otrzymuje się warunek brzegowy na wlocie do łożyska
|
|
3 π a4 n (pz - pw )
|
4 c³ L |
[ | 1 - ε cos |
( |
x
R |
) ] | 3 |
| (6.267)
|
Ponieważ (∂ p/∂ x) → 0 gdy ε → 0, więc - jest tego samego rzędu co ε. Oznacza to, że wyrażenie
jest rzędu ε² dla ε « 1.
Równanie (6.260) przyjmuje więc dla ε « l postać
|
∂² p
∂ z² |
+ |
∂² p
∂ x² |
= 0
| (6.268)
|
Funkcję ciśnienia można przedstawić w postaci iloczynu dwóch funkcji jednej zmiennej
|
p(x, z) = X(x) Z(z)
| (6.269)
|
z podstawienia tego uzyskuje się dwa zwykłe równania różniczkowe
|
∂² X
∂ x² |
+ K² X = 0 ; | |
∂² Z
∂ z² |
- K² Z = 0
| (6.270)
|
gdzie K jest stałą.
Zatem funkcja ciśnienia
| |
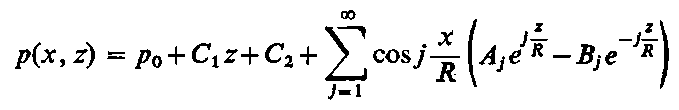
| (6.271)
|
W rozwiązaniu pominięto wyrażenie sin ( j x/R), albowiem funkcja p(x, z) ma być z założenia parzysta.
Ponieważ εcos(x/R) « 1 , dlatego można do równania (6.270) zastosować rozwinięcie dwumianowe
| |
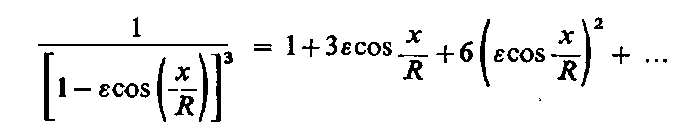
| (6.272)
|
Po pominięciu składników drugiego i wyższych rzędów ze względu na ε warunek graniczny (6.267) przyjmie postać
|
( |
∂ p
∂ z |
) |
w | = - ΛL |
( |
1 + 3 ε cos |
x
R |
) |
( pz - pw )
| (6.273)
|
przy czym
Wprowadzając do równania (6.271) warunki brzegowe można wyznaczyć stałe
|
C2 = - |
C1 L
2 | |
Bj = - Ajej (L/R)
|
Po podstawieniu stałych funkcji p( x, z ) przyjmie postać
| |
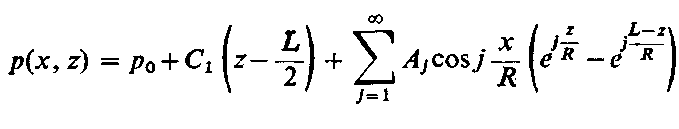
| (6.274)
|
skąd
| |
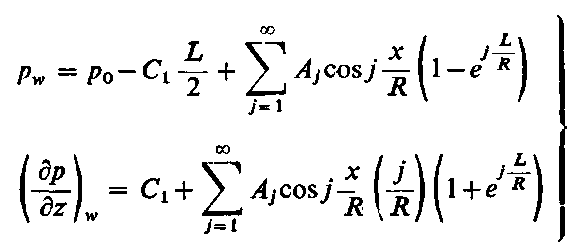
| (6.275)
|
Po podstawieniu równań (6.275) do równania (6.273) uzyskuje się
| |
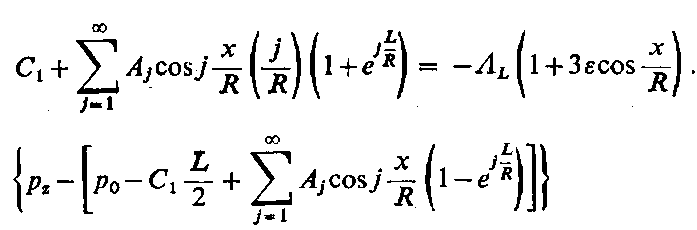
| (6.276)
|
skąd pomijając składniki wyższego rzędu ze względu na ε i A2, A3 … Ajoraz przyrównując tożsamościowe obie strony równania (6.276), otrzymuje się
| |
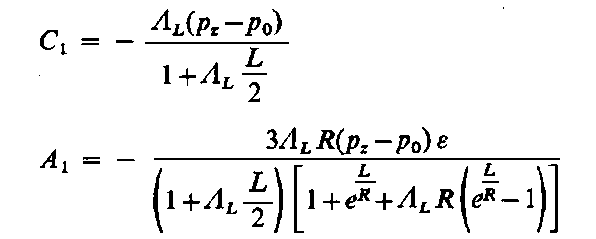
| (6.277)
|
Po podstawieniu wyznaczonych stałych do równania (6.274) można otrzymać poszukiwany rozkład ciśnienia dla ε « 1
| |
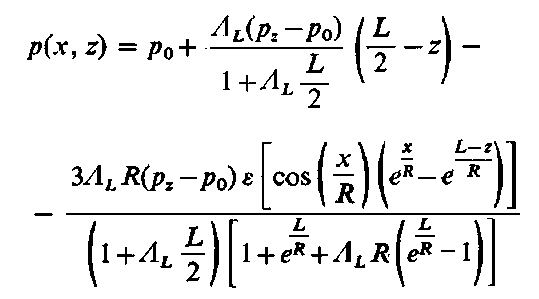
| (6.278)
|
Obciążalność łożyska jest określona ogólną zależnością
| |
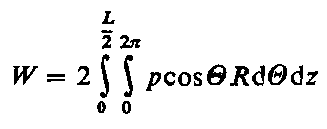
| (6.279)
|
Korzystając z wyznaczonego rozkładu ciśnienia można przeprowadzić całkowanie tego wyrażenia
| |
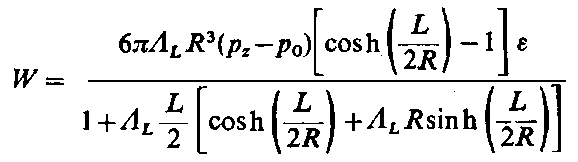
| (6.280)
|
oraz obliczyć nacisk jednostkowy
| |
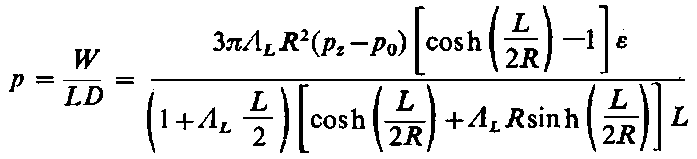
| (6.281)
|
Moc pompy potrzebna do doprowadzenia cieczy przez przewody zasilające do zasilania łożyska wynosi
| |
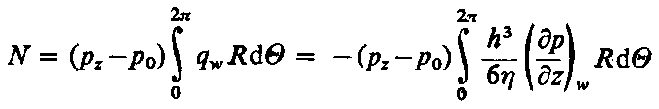
| (6.282)
|
Gradient ciśnienia na wlocie łożyska można wyznaczyć z równania (6.275) po podstawieniu stałych określonych zależnością (6.277)
| |
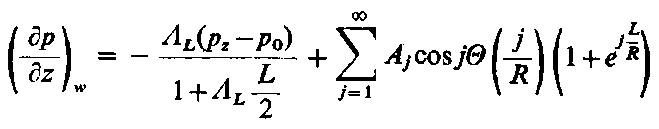
| (6.283)
|
Wyrażenie na grubość warstwy cieczy można rozwinąć następująco
|
h³ = c³ (1 - ε cos θ)³ = c³ (1 - 3 ε cos θ + …)
| (6.284)
|
Po podstawieniu obydwu ostatnich zależności do równania (6.282) na N, scałkowaniu go oraz pominięciu w tak otrzymanym wyrażeniu składników wyższego rzędu ze względu na małą wartość ε, otrzymuje się
| |
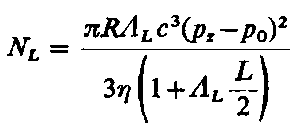
| (6.285)
|
Rugując z równań (6.282) i (6.285) czynnik (pz - p0) uzyskuje się
| |
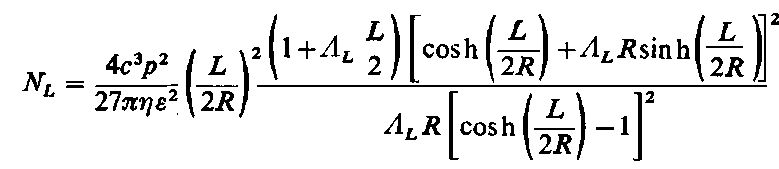
| (6.286)
|
Poszukując minimum NL względem ΛL otrzymuje się optymalną wartość ΛL
| |
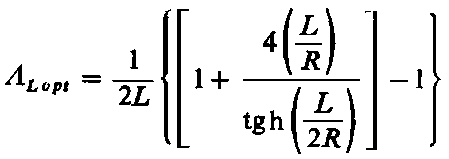
| (6.287)
|
W celu przeprowadzenia optymalizacji zapotrzebowania mocy NL względem L/D równanie (6.285) należy przedstawić w nieco zmienionej postaci
|
NL = |
c³ p²
108 π η ε² |
N0
| (6.288)
|
Przy takim założeniu N0 jest funkcją jedynie parametrów geometrycznych
| |
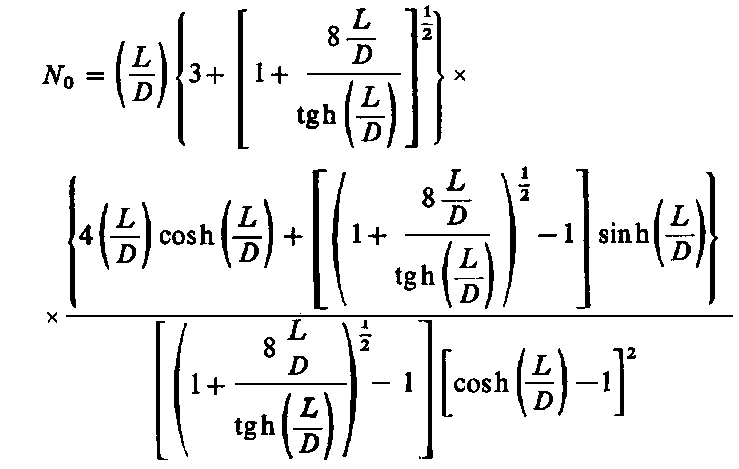
| (6.289)
|
Poszukując minimum N0 względem L/D otrzymuje się przy stosunku L/D = 1,1 minimalną wartość Nmin = 721. Daje to
|
NL min = 2,15 |
c³ p²
η ε²
| (6.290)
|
Rozwiązując równanie (6.285) przy stosunku L/D = 1,1 , otrzymuje się
|
(pz - p )opt = 2,13 |
p
ε
| (6.291)
|
Naprężenie ścinające w cieczy można wyznaczyć z równań (6.292) i (6.293)
|
τx = η ( |
∂ u
∂ y |
) |
y = 0 |
= η | ( | - |
U
h |
- |
1
2 η |
∂ p
∂ x |
h | )
| (6.292)
|
Ponieważ dla małych wartości ε pochodna (∂ p/∂ x) jest tego samego rzędu co ε, dlatego też siła tarcia T jest określona wzorem
| |
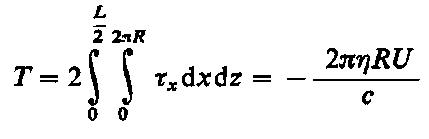
| (6.293)
|
Przedstawioną analizę przeprowadzono przy założeniu, że czop i panewka są współśrodkowe. Jeżeli występuje ruch względny między powierzchnią czopa a panewką, wówczas nastąpi połączenie smarowania hydrostatycznego z oddziaływaniem hydrodynamicznym. Prowadzi to do podwyższenia obciążalności skojarzenia w stosunku do wartości przewidzianych na podstawie przytoczonej analizy.
Podobnie jak wspomniano przy omawianiu smarowania hydrodynamicznego, także i rozwój wiedzy dotyczącej smarowania hydrostatycznego wykroczył daleko poza ramy przytoczonej klasycznej teorii.
Pełna analiza smarowania hydrostatycznego, uwzględniająca wiele zjawisk towarzyszących, pozwala opracować wytyczne umożliwiające prawidłowe zaprojektowanie i eksploatowanie łożyska.
6.7.3. Łożysko ślizgowe wzdłużne
Matematyczna analiza ślizgowych łożysk wzdłużnych smarowanych hydrostatycznie jest stosunkowo prosta w porównaniu z analogiczną analizą łożysk poprzecznych. Nie ma tu żmudnych wyprowadzeń, a wystarczy jedynie zastosowanie elementarnych
równań przepływu.
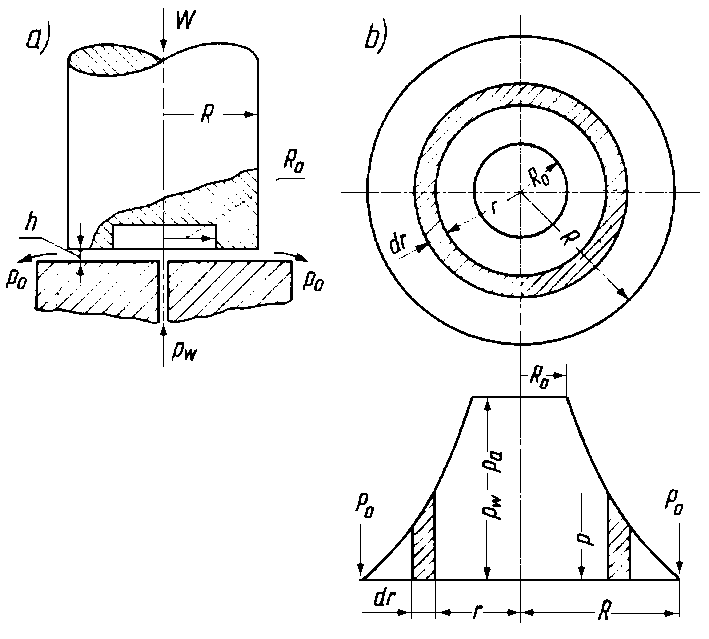 | |
Rys. 6.80. Łożysko ślizgowe wzdłużne stopowe: a) schemat łożyska, b) rozkład ciśnienia
|
Na rys. 6.80 podano przykład hydrostatycznego łożyskowania wału obciążonego osiową siłą W. Łożysko wykonano ze stopów metali. Wał o promieniu R ma na powierzchni czołowej wycięcie o promieniu R0. Ciecz jest doprowadzona pod ciśnieniem ( pw - pa) przez kanał umieszczony w środku łożyska. Następnie wypływa ona promieniowo na zewnątrz przez pierścieniową szczelinę o wysokości h. Ciśnienie cieczy na wylocie szczeliny ma wartość ciśnienia otoczenia p0. Rozkład ciśnienia cieczy w szczelinie można wyznaczyć z równania Reynoldsa. Zakreskowany na rys. 6.80b pierścień przedstawia elementarną szczelinę o szerokości 2 πr i długości dr. Podstawiając
otrzymuje się zależność na natężenie przepływu cieczy przepływającej przez zakreskowany obszar
|
Q = - |
h³ 2π r
12 η |
d p
d x
| (6.294)
|
znak (-) oznacza, że (d p/d r) jest ujemne.
Równanie to można przekształcić następująco
|
d p = |
6 η Q
π h³ |
d r
r
| (6.295)
|
Po scałkowaniu uzyskuje się
|
p = - |
6 η Q
π h³ |
ln r + C
| (6.296)
|
Stałą całkowania można wyznaczyć z warunku brzegowego
czyli
|
C = |
6 η Q
π h³ |
ln R + pa
| (6.297)
|
Po podstawieniu do (6.296) otrzymuje się
|
p - pa = |
6 η Q
π h³ |
ln |
R
r
| (6.298)
|
Z zależności tej można obliczyć wartość ciśnienia pw na wlocie do łożyska. Odpowiedni warunek brzegowy ma w tym przypadku następującą postać
czyli
|
pw - pa = |
6 η Q
π h³ |
ln |
R
R0
| (6.299)
|
Dzieląc równania (6.298) i (6.299) stronami otrzymuje się rozkład ciśnienia p w cieczy wzdłuż promienia r
|
p - pa = (pw - pa) |
| (6.300)
|
Wyznaczając obciążalność łożyska należy uwzględnić to, że całkowita siła nośna składa się z siły wywieranej przez ciecz o ciśnieniu (pw - p0) na powierzchnię wgłębienia o promieniu R0 oraz z siły wywieranej przez wypływającą ciecz o zmiennym ciśnieniu (pw - p0) na powierzchnię progu łożyska. Uwzględniając powyższe zależności otrzymuje się
| |
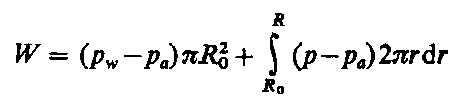
| (6.301)
|
Funkcja (pw - p0) jest dana równaniem (6.300), a stąd
| |
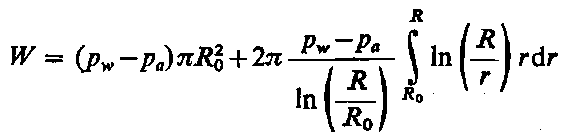
| (6.302)
|
Po scałkowaniu otrzymuje się następujące wyrażenie na obciążalność
Natężenie przepływu można wyznaczyć z równania (6.294) przekształcając je do postaci
Równania (6.303) i (6.304) wiążą ze sobą podstawowe parametry łożyska, jak: grubość warstewki cieczy h oraz wymiary geometryczne R0 i R z ciśnieniem cieczy, natężeniem przepływu i obciążalnością. Stanowią one więc wystarczającą informację dotyczącą prawidłowości zaprojektowania i eksploatowania łożyska. Na rys. 6.81 przedstawiono orientacyjne zależności obciążalności hydrostatycznego łożyska wzdłużnego od jego wymiarów geometrycznych i ciśnienia zasilania.
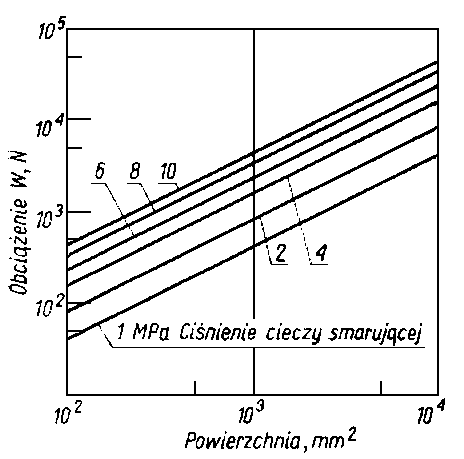 |
Rys. 6.81. Obciążalność wzdłużnego łożyska ślizgowego, smarowanego hydrostatycznie w funkcji pola powierzchni oporowej i ciśnienia zasilania
|
Podobnie jak analogiczne zależności dla łożyska poprzecznego, tak i te zależności zostały sporządzone przy założeniu określającym relację ciśnienia na wlocie i średniego nacisku jednostkowego na powierzchnię łożyska. Ciśnienie na wlocie musi być co najmniej czterokrotnie większe od średniego nacisku jednostkowego na powierzchnię łożyska. Reguła ta jest także powszechnie stosowana w praktyce do orientacyjnego oszacowania obciążalności łożyska wzdłużnego smarowanego hydrostatycznie.
Wymagania dotyczące układów zasilania łożysk wzdłużnych są podobne do odpowiednich wymagań dla łożysk poprzecznych. Także i tu muszą być ściśle spełnione warunki dotyczące natężenia przepływu i ciśnienia zasilania. Na rys. 6.82 przedstawiono dwa typowe układy smarowania łożysk wzdłużnych, tj. układ ze stałym natężeniem przepływu oraz układ ze stałym ciśnieniem zasilania. Układ ze stałym natężeniem przepływu składa się z wysokociśnieniowej pompy, która podaje ciecz przy stałym natężeniu przepływu, niezależnie od ciśnienia w przestrzeni smarującej. Układ ze stałym ciśnieniem zasilania oprócz pompy ma zawór regulujący ciśnienie oraz element wyrównawczy, najczęściej rurkę kapilarną lub kryzę.
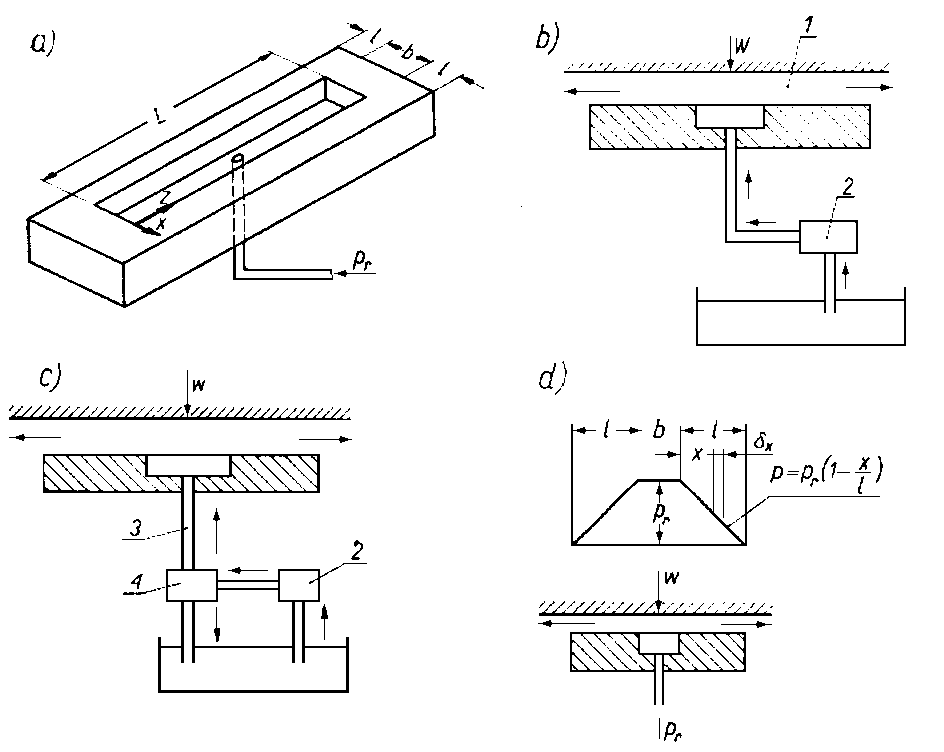 |
Rys. 6.82. Układy smarowania hydrostatycznego:
- płytka oporowa,
- układ ze stałym natężeniem przepływu,
- układ ze stałym ciśnieniem zasilania,
- rozkład ciśnienia w szczelinie;
- warstwa cieczy smarującej,
- pompa,
- element kompensujący,
- ciśnieniowy zawór kontrolny,
W- obciążenie
|
Zastosowanie elementów regulujących parametry przepływu cieczy ma głównie za zadanie polepszenie adaptacji łożyska do nowych warunków pracy przy zmianach obciążenia. Charakterystyką ilościową, opisującą zdolność adaptacyjną łożyska, jest czułość warstwy cieczy smarującej na zmianę obciążenia. Dla przykładu przedstawionego na rys. 6.82a zależność taka ma następującą postać
| |
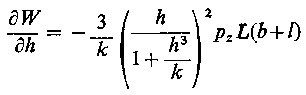
| (6.305)
|
przy czym
gdzie: W - obciążenie w N, h - grubość warstwy cieczy smarującej w m, p - ciśnienie pompy (zasilanie) w Pa, d-średnica rurki kapilarnej w m, lt - długość rurki kapilarnej w m, l, h, L - wymiary łożyska wg rysunku.
Z równania (6.305) wynika, że czułość grubości warstwy cieczy na zmianę obciążenia, zależy od jej grubości, ciśnienia zasilania oraz wymiarów geometrycznych kapilary i łożyska. Z zależności tej wynika więc możliwość kształtowania zdolności adaptacyjnej łożyska przez odpowiedni dobór parametrów układu zasilania.
6.8. Smarowanie gazodynamiczne
Smarowanie gazodynamiczne charakteryzuje się tym, że między odpowiednio ukształtowanymi powierzchniami znajdującymi się we względnym ruchu tworzy się warstwa gazu, całkowicie oddzielająca te powierzchnie, w której powstaje dynamiczne ciśnienie równoważące zewnętrzne obciążenie.
Z definicji wynika, że zasada smarowania gazodynamicznego jest analogiczna do zasady smarowania hydrodynamicznego. Jednak ze względu na to, że substancją smarującą jest tu płyn ściśliwy, istnieją różnice w stosunku do smarowania cieczą, którą można uznać za nieściśliwą. Różnice te są omówione w następujących punktach.
Rozkład ciśnienia. W warstwie cieczy powstającej przy smarowaniu hydrodynamicznym tworzy się nadciśnienie, a więc ciśnienie większe od ciśnienia otoczenia, oraz podciśnienie, czyli ciśnienie mniejsze od ciśnienia otoczenia pa. Wartość tych wzrostów i spadków ciśnienia jest niezależna od wartości ciśnienia otoczenia. W przeciwieństwie do tego przy smarowaniu gazodynamicznym, zmiany ciśnienia są zależne od wartości ciśnienia otoczenia pa. Dlatego przy analizie smarowania gazodynamicznego konieczne jest uwzględnienie w równaniu Reynoldsa bezwzględnego ciśnienia gazu.
Jednakże oczywiste jest to, że przy rozpatrywaniu rozkładu ciśnienia przy smarowaniu gazodynamicznym w układzie odniesienia służącym do analizy hydrodynamicznej, tzn. w stosunku do ciśnienia otoczenia pa, wystąpią również obszary podciśnienia i nadciśnienia. W łożyskach smarowanych gazodynamicznie, ze względu na ciągłość przepływu gazu, na całym obwodzie obszar podciśnienia stanowi dopełnienie do kąta 2π. Zjawisko to jest pożyteczne ponieważ strefa podciśnienia zwiększa nośność łożyska. Powoduje ono odciążenie wału przez działanie ssące w obszarze przeciwległym do obszaru podwyższonego ciśnienia. Typowy rozkład ciśnienia przy smarowaniu gazodynamicznym łożyska poprzecznego przedstawiono na rys. 6.83.
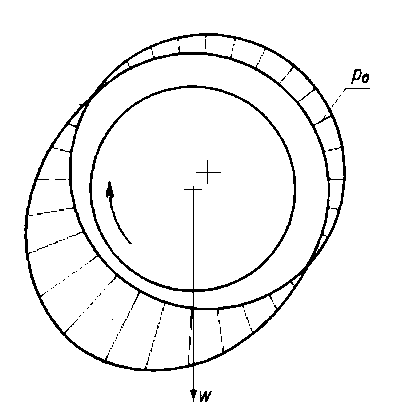 |
Rys. 6.83. Rozkład ciśnienia na obwodzie gazodynamicznego ślizgowego łożyska poprzecznego z pełną panwią
|
Zmiany gęstości. W analizie smarowania gazodynamicznego konieczne jest uwzględnienie zmian gęstości gazu. W tabl. 6.11 podano wpływ ściśliwości gazu na charakterystyki łożyska. Występują tu wyraźne rozbieżności między danymi eksperymentalnymi a teorią płynów nieściśliwych zastosowaną do smarowania gazem.
Przytoczone wyniki teoretyczne dotyczą powietrza traktowanego jako płyn nieściśliwy przy założeniu, że jego gęstość jest stała, równa gęstości w warunkach otoczenia. Teorię płynów nieściśliwych można wykorzystywać do oceny właściwości łożysk smarowanych gazodynamicznie tylko przy bardzo małych (zbliżonych do zera) wartościach parametru łożyska
|
Λ = |
6 η ω
pa |
( |
R
c |
)²
| (6.306)
|
gdzie: η - lepkość w Pa • s, ω - prędkość kątowa w l /s, R - promień czopa w m, c - luz promieniowy w m.
Zmiany lepkości. Lepkość gazu wzrasta ze wzrostem temperatury w przeciwieństwie do lepkości cieczy. Zazwyczaj w analizie smarowania gazodynamicznego zakłada się izotermiczne warunki pracy. Założenie to jest możliwe do przyjęcia dla średnich prędkości, przy których straty tarcia są małe i nie powodują dużego wzrostu temperatury. Przy dużych prędkościach konieczne jest uwzględnienie w równaniu Reynoldsa zmian lepkości związanych ze zmianą temperatury.
Zaburzenia przepływu. W łożyskach gazodynamicznych nie występują zaburzenia przepływu tego typu, jak w łożyskach hydrodynamicznych. Upraszcza to znacznie warunki brzegowe. Jednakże w szczególnych przypadkach pojawiają się inne odstępstwa od teorii ciągłego przepływu. Jeżeli grubość warstwy smarującej staje się porównywalna ze średnią drogą swobodną cząsteczek gazu, wówczas prze-
Tablica 6.11. Charakterystyki łożyska ślizgowego z uwzględnieniem ściśliwości oleju
n obr/min
u cm/s
ε | 230
182,9
0,39 | 805
641,3
0,1625 | 1730
1377,9
0,091 | |
Wartość | doświadczalna | teoretyczna | doświadczalna | teoretyczna | doświadczalna | teoretyczna | |
p0-pa, kPa | 536,13 | 555,45 | 301,53 | 689,60 | 301,53 | 880,6 | |
pmin-pa, kPa | -407,10 | -555,45 | -325,68 | -689,60 | -349,83 | -808,68 | |
p0-pmin, kPa | 943,23 | 1110,9 | 627,21 | 1380 | 651,36 | 1617,36 | |
θ0-180, stopnie | -28 | -57 | -43 | -76 | -43 | -82 | |
θmin-180, stopnie | 51 | 57 | 96 | 76 | 129 | 82 | |
θmin-θmin, stopnie | 79 | 114 | 139 | 152 | 172 | 164 |
|
n- | prędkość obrotowa, obr/min, | |
u- | prędkość obwodowa czopa, cm/s, | |
ε- | mimośrodowość względna, | |
p0- | ciśnienie maksymalne w szczelinie smarowej, kPa, | |
pa- | ciśnienie zasilania, kPa, | |
pmin- | ciśnienie w szczelinie smarowej przy minimalnej grubości warstwy oleju, kPa, | |
θ0- | kąt określający ciśnienie maksymalne względem obciążenia normalnego, stopnie, | |
θmin- | kąt określający minimalną grubość warstwy oleju względem obciążenia normalnego, stopnie. |
| |
Dokładność wykonania. Warstwy smarujące gazu powstające podczas smarowania gazodynamicznego są dużo cieńsze niż analogiczne warstwy przy smarowaniu cieczą. Ich grubość jest często tego samego rzędu co chropowatość powierzchni czopa i panewki. Dokładność wykonania i chropowatość współpracujących powierzchni wpływa więc zasadniczo na efektywność ich oddzielenia za pomocą warstwy smarującej. Wszelkie błędy kształtu takich powierzchni powodują na przemian ściskanie i rozszerzanie gazu. Na skutek tego w warstwie gazu powstają obszary podwyższonych i obniżonych ciśnień, które zniekształcają rozkład ciśnienia i pozostałe parametry przepływu.
Przenoszenie ciepła. Ze względu na małe straty spowodowane ścinaniem ilość odprowadzanego ciepła z łożysk smarowanych gazodynamicznie jest mniejsza niż z łożysk smarowanych hydrodynamicznie. Dlatego uwzględnianie wpływu zjawisk cieplnych ma znaczenie tylko przy bardzo dużych prędkościach.
Reasumując należy stwierdzić, że chociaż stała lepkość i mniej skomplikowane warunki brzegowe upraszczają analizę łożysk smarowanych gazodynamicznie, to jednak konieczność uwzględnienia zmian gęstości stanowi znaczne jej utrudnienie. Nawet przy zastosowaniu idealnych zależności gazodynamiki otrzymuje się trudne do rozwiązania równania różniczkowe nieliniowe.
Wykorzystując zależności dla gazu doskonałego równanie Reynoldsa można przedstawić następująco
| |
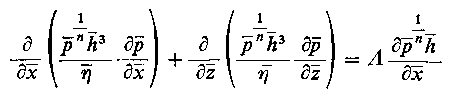
| (6.307)
|
przy czym
|
Λ = |
6 η ω
pa |
( |
R
c |
)² ; | |
p = |
p
pa | ; | |
h = |
h
h2 |
|
|
η = |
η
η0 | ; |
x = |
x
R | ; |
z = |
z
R
| (6.308)
|
gdzie: n-wykładnik politropy, η0-lepkość w warunkach otoczenia w Pa•s, pa - ciśnienie otoczenia w Pa, h2 - grubość warstwy, przy której wartość ciśnienia dynamicznego spada do pa w m (rys. 6.83), pozostałe oznaczenia jak w dotychczasowych rozważaniach.
Równanie (6.307) można przekształcić następująco
| |
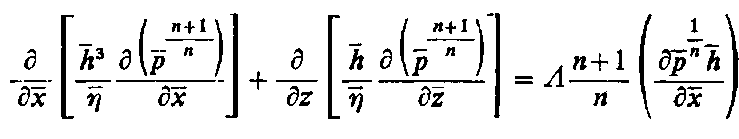
| (6.309)
|
Dla warunków izotermicznych (n = l) zależność tę można zredukować do postaci
| |
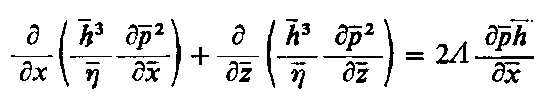
| (6.310)
|
Równanie (6.310) ma postać identyczną jak równanie (6.309) dla smarowania cieczami. Rozwiązanie słuszne dla cieczy można więc wykorzystać do analizy smarowania gazem. Konieczne jest przy tym jednak ustalenie zależności między p² i 2p h dla gazu oraz p i h dla cieczy. Dla bardzo małych wartości tych parametrów, bliskich zeru, rozkład ciśnienia i obciążalność warstwy gazu można uzyskać z rozwiązania dla smarowanych cieczą łożysk o skończonych wymiarach. Przy bardzo dużych wartościach L rozwiązanie problemu smarowania aerodynamicznego jest natomiast zbliżone do rozwiązania dla nieskończenie długiego łożyska smarowanego cieczą. Ponieważ ciśnienie p musi mieć wartość skończoną, dlatego z warunku Λ → ∞ wynika warunek
| |
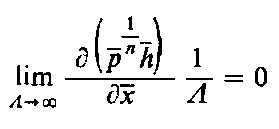
| (6.311)
|
bowiem tylko wtedy jest możliwe istnienie skończonej granicy prawej strony równania (6.310).
Z warunku tego wynika
gdzie: a = h1, h1 - grubość warstwy, przy której rozpoczyna się wzrost ciśnienia dynamicznego powyżej wartości pa w m, h2 - grubość warstwy, przy której kończy się spadek ciśnienia dynamicznego do wartości pa, w m.
Dla dużych wartości Λ obciążalność w bardzo małym stopniu zależy od prędkości i dąży asymptotycznie, przy Λ → ∞, do wartości
| |
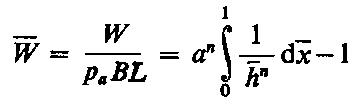
| (6.313)
|
Postęp wiedzy w zakresie działania łożysk smarowanych gazodynamicznie doprowadził w ostatnim piętnastoleciu do ich rozpowszechnienia w szerokim zakresie w wielu gałęziach przemysłu.
Ideę zastosowania gazu jako substancji smarującej zaproponował po raz pierwszy Hirn już w 1854 r. Dopiero jednak w 1897 r. Kingsbury skonstruował pierwsze łożysko smarowane gazem. Współcześnie łożyska gazodynamiczne są w szerokim zakresie stosowane w maszynach przepływowych, we wrzecionach obrabiarek, w urządzeniach kontrolno-pomiarowych, w żyroskopach i w wiertarkach dentystycznych.
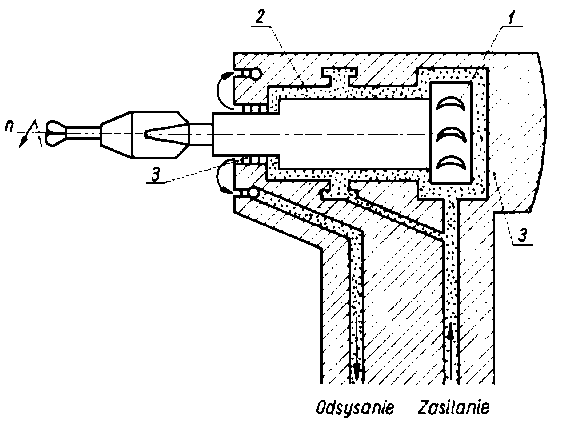 |
Rys. 6.84. Smarowanie gazodynamiczne i gazostatyczne łożysk wrzeciona wiertarki dentystycznej ;
- - turbina,
- - łożysko gazodynamiczne,
- - łożysko gazostatyczne,
n = 420 000 obr/min
|
Na rys. 6.84 podano przykład zastosowania smarowania powietrzem łożysk wrzeciona wiertarki dentystycznej. Prędkość obrotowa wrzeciona n wynosi 420000 obr/min, a wydajność powietrza 2040 dm³/s, przy ciśnieniu zasilania 0,36 MPa (3,5 at). Zalety decydujące o rozpowszechnieniu smarowania gazem są następujące: małe opory tarcia, dostępność substancji, niezanieczyszczanie powierzchni łożyska, możliwość stosowania w szerokim zakresie temperatury w przeciwieństwie do cieczy, której zastosowanie jest ograniczone ze względu na niebezpieczeństwo jej wrzenia czy zamarzania.
Smarowanie gazodynamiczne ma jednak i poważne wady, jak: mała nośność (ciśnienie w łożyskach gazodynamicznych jest rzędu 105 Pa w porównaniu z wartościami rzędu 107 Pa przy smarowaniu hydrodynamicznym), mała stabilność pracy, duże wymagania w zakresie dokładności wykonania i chropowatości powierzchni.
Łożyska gazodynamiczne mogą być wykonywane jako wzdłużne i poprzeczne (rys. 6.85).
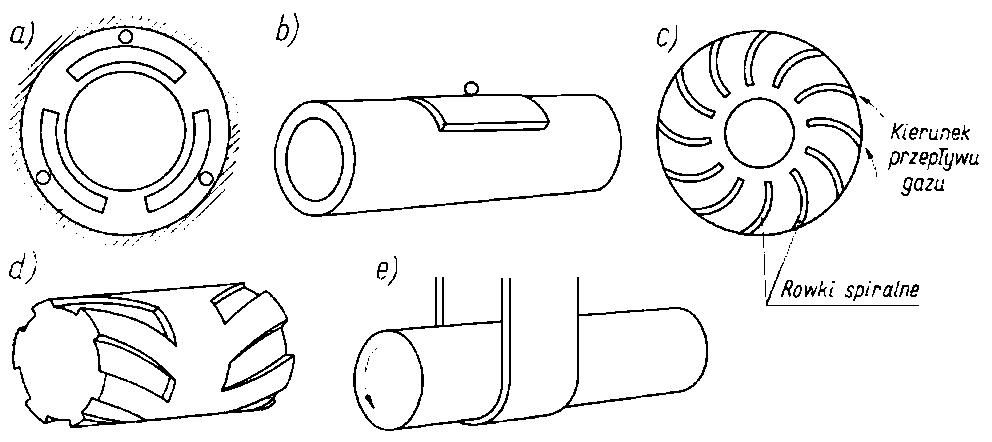
Rys. 6.85. Łożyska gazodynamiczne:
a, b) łożyska z wahliwymi płytkami panwiowymi,
c) łożyska wzdłużne ze spiralnymi rowkami,
d) łożysko poprzeczne ze spiralnymi rowkami,
e) łożysko foliowe
|
6.9. Smarowanie gazostatyczne
Smarowanie gazostatyczne charakteryzuje się tym, że między współpracującymi powierzchniami, znajdującymi się we względnym spoczynku, tworzy się warstwa gazu całkowicie oddzielająca te powierzchnie, w której powstaje statyczne ciśnienie występujące na skutek ciągłego krążenia gazu pod wpływem oddziaływania ciśnienia, wytwarzanego przez odpowiednie źródło, równoważącego zewnętrzne obciążenie.
Zjawiska fizyczne stanowiące o istocie smarowania (dynamiczne lub statyczne oddziaływanie substancji smarującej) są jednakowe. Różnice między smarowaniem cieczą a smarowaniem gazem są jedynie ilościowe i dotyczą głównie wartości lepkości, gęstości oraz ich zmian. Natomiast wady i zalety smarowania gazodynamicznego są identyczne, jak smarowania hydrodynamicznego.
Zasada smarowania gazodynamicznego jest często demonstrowana za pomocą łożyska (rys. 6.86). Składa się ono z podstawy z wgłębieniem w kształcie czaszy kulistej oraz z metalowej kuli. Opór tarcia w takim łożysku jest niezwykle mały.
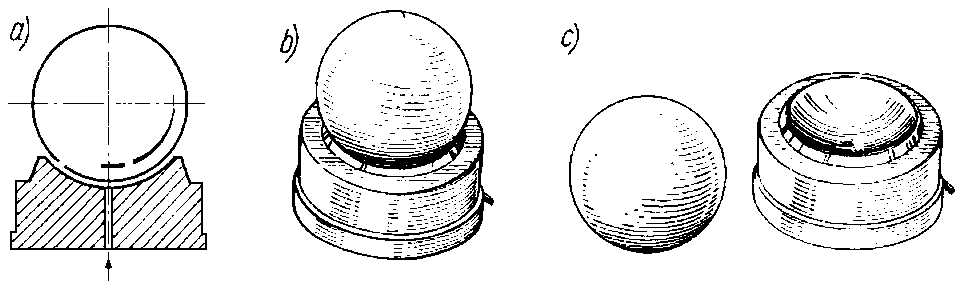
Rys. 6.86. Model łożyska gazostatycznego:
a) przekrój,
b) widok ogólny,
c) elementy łożyska
|
Dzięki temu kulę można swobodnie obracać. Utrzymuje ona swój ruch przez długi czas po zlikwidowaniu siły wymuszającej.
Natężenie przepływu potrzebne do wytworzenia warstwy smarującej, oddzielającej całkowicie współpracujące powierzchnie, jest stosunkowo niewielkie. Dla kuł o masie ok. 15 kg wynosi ono jedynie 0,75 dm³/min przy ciśnieniu zasilania zaledwie 0,015 MPa (0,15 at).
Analiza smarowania gazostatycznego opiera się, ze względu na podobieństwo zjawisk, na tych samych zasadach, co analiza smarowania hydrostatycznego. Z rozważań przeprowadzonych dla smarowania hydrostatycznego wynika, że zależności opisujące smarowanie łożysk poprzecznych są zdecydowanie bardziej skomplikowane niż odpowiednie zależności dla łożysk wzdłużnych, charakteryzujące się wyjątkowo prostym opisem analitycznym. Dlatego też ze względów dydaktycznych będzie omówiony przypadek, jako bardziej interesujący, smarowanego gazostatycznie ślizgowego łożyska poprzecznego z uwzględnieniem analogii do smarowania hydrostatycznego.
Równanie Reynoldsa jest słuszne dla płynów nieściśliwych i ściśliwych. Korzystając z równania stanu dla gazu idealnego o warunkach izotermicznych ( (p/r) =const) oraz zakładając warunki brzegowe V = U1 = U2 = 0, można równanie Reynoldsa przekształcić do postaci
| |
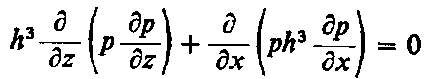
| (6.314)
|
skąd, po zróżniczkowaniu i podstawieniu wyrażeń na grubość warstwy smarującej h otrzymuje się dla łożyska poprzecznego
| |
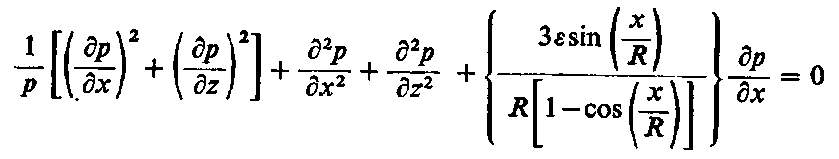
| (6.315)
|
Uwzględniając powyższe zależności równanie Reynoldsa można przedstawić następująco
| |
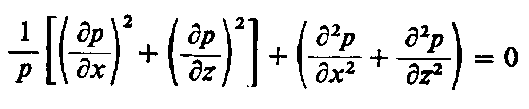
| (6.316)
|
Wprowadzając pomocniczą zmienną pˆ określoną zależnością
| |
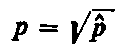
| (6.317)
|
można równanie (6.316) przedstawić w postaci
| |
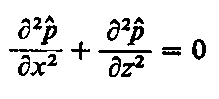
| (6.318)
|
Warunek brzegowy jest dla rozwiązywanego równania następujący
| |
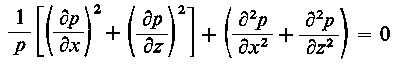
|
|
Przy powyższych założeniach rozwiązanie równania (6.318) jest określone zależnością (6.316). Podstawiając do równania λ = ΛL½L uzyskuje się rozwiązanie równania (6.318) jako funkcję pomocniczej zmiennej pˆ
| |
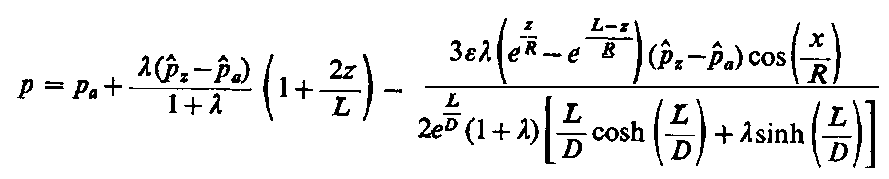
| (6.319)
|
W analizie łożysk gazostatycznych wygodne jest stosowanie wielkości względnych, odniesionych do ciśnienia otoczenia pa. W dalszych rozważaniach wielkości takie będą oznaczane poziomą kreską umieszczoną nad symbolem wielkości, np. pz - względne ciśnienie zasilania.
Dokonując odwrotnej transformacji zmiennych oraz pomijając wyrażenia drugiego i wyższych rzędów ze względu na małe wartości ε, otrzymuje się rozwiązanie równania opisującego smarowanie gazostatyczne
| |
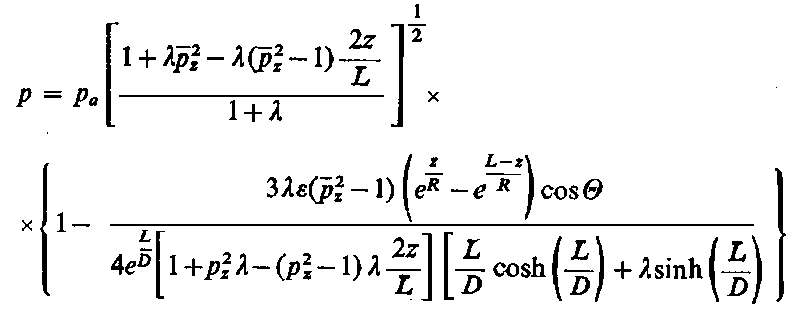
| (6.320)
|
gdzie pz = (pz/pa) - względne ciśnienie zasilania.
Równanie (6.320) wyznacza poszukiwany rozkład ciśnienia p( z, 0 ). Całkując je po powierzchni łożyska można określić nośność łożyska
| |
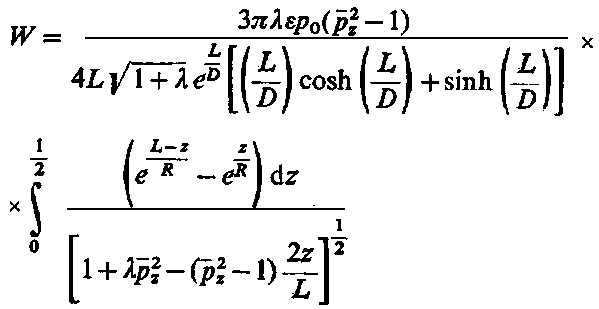
| (6.321)
|
Całkę występującą w równaniu (6.321) można obliczyć podstawiając
oraz korzystając z całek Gaussa
| |
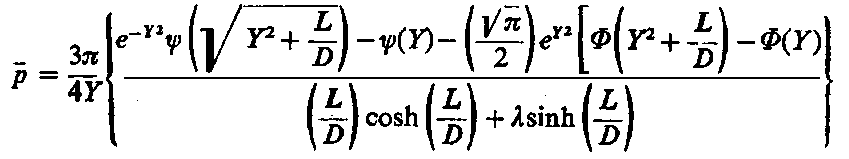
| (6.322)
|
przy czym
zaś p = (p/paε) - względna nośność. Równanie (6.322) można także przedstawić następująco:
| |
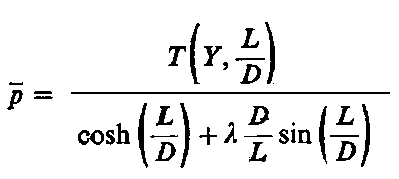
| (6.323)
|
przy czym T(Y, L/D) jest funkcją zmiennych Y oraz (L/D) daną w postaci
| |
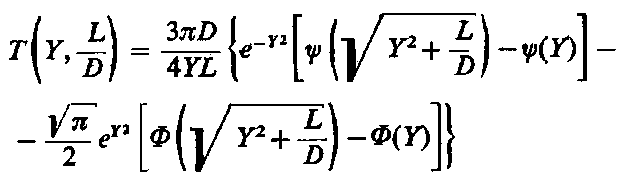
| (6.324)
|
Zależność wartości funkcji T(Y, L/D) od zmiennej Y dla różnych wartości stosunku - przedstawiono na rys. 6.87. Zamieszczone na tym rysunku wykresy umożliwiają na podstawie równania (6.321) dobranie odpowiednich wartości λ przy założonym stosunku ciśnień pz (lub odwrotnie), a następnie wyznaczenie z równania (6.322) względnej nośności p. Z równania (6.322) można także wyznaczyć optymalną wartość λopt przez podstawienie w miejsce Y i wielkości Yopt oraz (L/D)opt
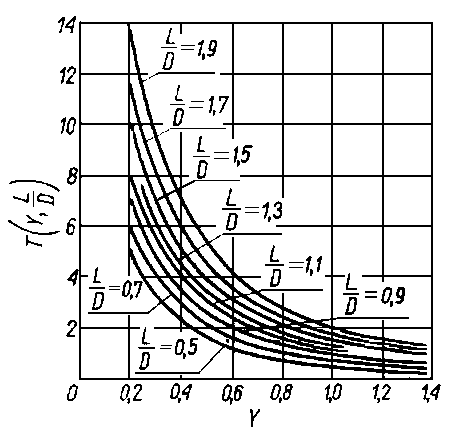 |
Rys. 6.87. Zależność funkcji F(Y, L/D) od Y dla różnych wartości (L/D)
|
| |
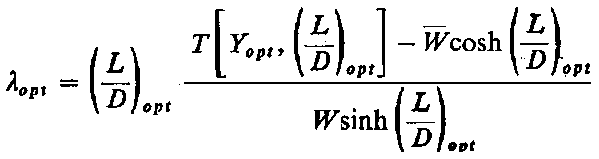
| (6.325)
|
Optymalną wartość względnego ciśnienia zasilania można określić z równania
| |
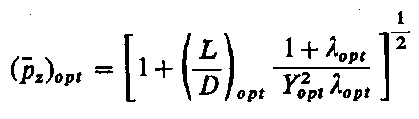
| (6.326)
|
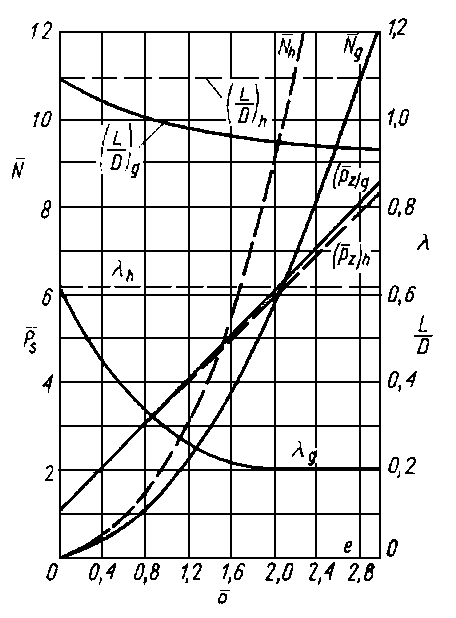 |
Rys. 6.88. Porównanie charakterystyk łożysk hydrostatycznych i gazostatycznych; h- smarowanie hydrostatyczne, g - smarowanie gazostatyczne
|
Równanie (6.326) służy za podstawę do graficznego przedstawienia następujących zależności:
| |
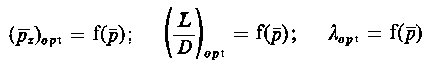
| (6.327)
|
Funkcje te przedstawiono na rys. 6.88. Na wykresie tym podano także zależność względnego zapotrzebowania mocy N = (N/paε) od względnej nośności. Oprócz oznaczonych indeksem g wyników dotyczących smarowania gazostatycznego, zamieszczono na rysunku także, dla porównania, krzywe wyróżnione indeksem h, opisujące smarowanie hydrostatyczne. Przytoczone zależności analityczne oraz wykresy przedstawione na rys. 6.88 pozwalają określić wartości podstawowych wielkości charakteryzujących smarowanie gazostatyczne. Podobnie jak w poprzednich rozdziałach, w których omówiono pozostałe rodzaje smarowania płynnego, tak i tu, informacje dotyczące konstrukcji nieodłącznie są związane z informacjami dotyczącymi technologii i eksploatacji, tworząc złożoną całość, którą należy rozpatrywać kompleksowo.
6.10. Smarowanie elastohydrodynamiczne
Smarowanie elastohydrodynamiczne jest przypadkiem tarcia płynnego przy styku kontaktowym (Hertza). Przy smarowaniu elastohydrodynamicznym pod wpływem wysokich ciśnień występują duże zmiany lepkości oraz znaczne odkształcenia współpracujących elementów.
6.10.1. Zasada smarowania elastohydrodynamicznego
W warunkach smarowania hydrodynamicznego, np. w większości łożysk ślizgowych, współpracujące powierzchnie są oddzielone całkowicie warstwą substancji smarującej. Do połowy lat dwudziestych naszego stulecia uważano, że przy istnieniu oddziaływań naprężeń kontaktowych (koła zębate, łożyska toczne itp.) smarowanie hydrodynamiczne nie może występować. Pogląd ten opierał się na wnioskach wyciągniętych z klasycznej teorii hydrodynamicznej zakładającej, że grubość warstwy cieczy jest niewystarczająca do oddzieleni nierówności powierzchni nawet w warunkach szczególnie sprzyjających. Za podstawę analizy brano lepkość cieczy wchodzącej w strefę styku bez uwzględnienia zmian lepkości związanych z działaniem wysokich ciśnień w strefie styku kontaktowego. Jednak długotrwała praca wielu przekładni zębatych przy minimalnych efektach zużycia sugerowała istnienie innej warstwy niż graniczna, oddzielającej całkowicie współpracujące powierzchnie. W rzeczywistości w kołach zębatych i łożyskach tocznych występuje specyficzna, odmienna niż w łożyskach ślizgowych, forma smarowania hydrodynamicznego, zwana smarowaniem elastohydrodynamicznym.
Klasyczna teoria smarowania hydrodynamicznego (Reynoldsa) opierała się na wielu założeniach upraszczających. Do najważniejszych z nich należą:
- stała lepkość oleju znajdującego się pomiędzy współpracującymi powierzchniami,
- nieodkształcalność (idealna sztywność) współpracujących powierzchni.
Założenia te odpowiadają z grubsza warunkom pracy łożysk ślizgowych, lecz nie można ich jednak odnieść do styku kontaktowego Hertza.
Począwszy od 1940 r. wielu badaczy usiłowało zmodyfikować klasyczną teorię hydrodynamiczną stosując ją do styków kontaktowych. Powszechnie zgadzano się, że grubość przewidywanej warstwy hydrodynamicznej wzrasta dwu lub trzykrotnie, jeżeli uwzględnić wzrost lepkości oleju pod ciśnieniem w styku. Nie było to jednak wystarczające wytłumaczenie występowania w kołach zębatych i łożyskach tocznych tarcia płynnego. Dalsze prace wykazały istnienie zjawiska sprężystego odkształcenia powierzchni współpracujących, wywołanego dużym ciśnieniem w warstwie cieczy.
Pierwsze prace teoretyczne, będące podstawą zmodyfikowanej teorii smarowania hydrodynamicznego, nazwanej później teorią smarowania elastohydrodynamicznego, opublikowali w latach 1949-1951 Grubin i Petrusewicz. Zgodnie z ich analizą powierzchnie współpracujące stają się w obszarze styku, w czasie jego trwania, w przybliżeniu równoległe, przy czym w obszarze tym rozkład ciśnienia jest zbliżony do rozkładu nacisków Hertza. Na krańcu obszaru styku kształt zdeformowanej sprężyście powierzchni implikuje gwałtowną zmianę wartości ciśnienia cieczy. Na rys. 6.89 przedstawiono kształt warstwy elastohydrodynamicznej, zaś na rys. 6.89b - rozkład ciśnienia wg Grubina i Petrusewicza.
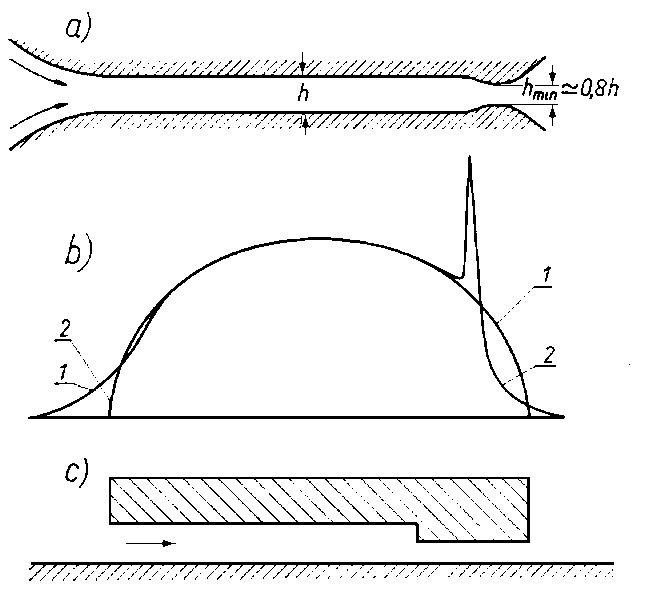 |
Rys. 6.89. Charakterystyki styku elastohydrodynamicznego:
a) kształt warstwy cieczy smarującej,
b) rozkład ciśnienia,
c) łożysko Rayleigha;
1-styk niesmarowany,
2 - styk smarowany
|
Wykonane następne doświadczenia wykazały, że grubość warstwy smarującej jest nieznacznie zależna od obciążenia. W 1958 r. Crook przedstawił bezpośrednią metodę pomiaru grubości elastohydrodynamicznej warstwy cieczy w urządzeniu odtwarzającym współpracę dwóch walców. Stwierdził on, że zmiana obciążenia wpływa nieznacznie na grubość warstwy smarującej, zgodnie z analizą Grubina.
Badania smarowania elastohydrodynamicznego wskazały na interesującą analogię między optymalnym kształtem ślizgacza łożyska wzdłużnego a kształtem warstwy elastohydrodynamicznej. Przy styku kontaktowym powierzchnie przyjmują kształt zbliżony do optymalnego (optymalna nośność) kształtu Rayleigha zgodnie z zasadą Le Chateliera-Brauna.
Odkształcenia sprężyste powierzchni i wzrost lepkości cieczy w strefie styku jest przykładem nakładania się zjawisk i sumowania ich skutków. W tabl. 6.12 przedstawiono porównanie nośności warstwy elastohydrodynamicznej z wartościami obliczonymi na podstawie kolejnych modyfikacji teorii hydrodynamicznej. Nośność jest tu wyrażona przez siłę przypadającą na jednostkę długości styku zębów smarowanej pary kół zębatych.
Tablica 6.12. Porównanie nośności warstw smarujących|
Założenia teorii | Nośność
kN/m | |
Nieodkształcalność ciał smarowanych i stała lepkość | 236 | |
Uwzględnienie zmian lepkości w strefie styku | 512 | |
Uwzględnienie odkształceń sprężystych powierzchni | 946 | |
Teoria elastohydrodynamiczna | 8055
| |
6.10.2. Geometria styku kontaktowego
Styk wielu powierzchni elementów maszyn można przedstawić modelowo za pomocą powierzchni cylindrycznych. Transformacja taka daje dobrą zgodność geometryczną dla nieodkształconych ciał w bezpośrednim sąsiedztwie styku.
W przypadku łożysk wałeczkowych (rys. 6.90) kształty stykających się elementów są dokładnie cylindryczne. Na bieżni wewnętrznej styk jest utworzony
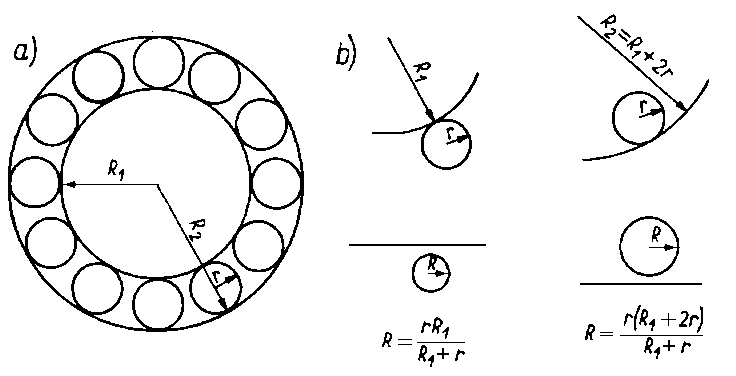
Rys. 6.90. Cylindry równoważne dla łożyska wałeczkowego:
a) schemat łożyska,
b) współpracujące elementy łożyska, i cylindry równoważne
|
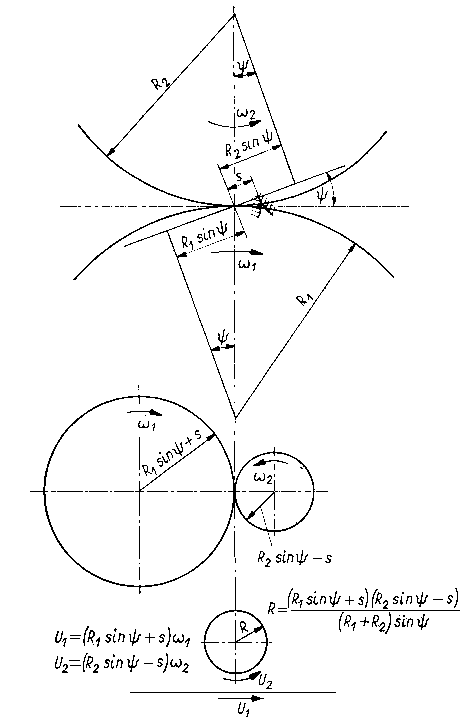 |
Rys. 6.91. Cylindry równoważne dla zębów o zarysie ewolwentowym
|
przez dwie zewnętrzne powierzchnie cylindryczne o promieniach R1 i r, natomiast na bieżni zewnętrznej styk istnieje między zewnętrzną powierzchnią cylindryczną wałeczka o promieniu r a wewnętrzną, wklęsłą powierzchnią cylindryczną bieżni o promieniu R1 + 2r.
Dla kół zębatych o zębach ewolwentowych można wykazać, że styk w odległości s od środka przyporu (rys. 6.91) można przedstawić przez dwa cylindry obracające się z prędkościami kątowymi ω1 i ω2 o promieniach
|
R1 sin ψ + s | ; |
R1 sin ψ - s
| (6.328)
|
gdzie ψ przyporu.
Przedstawiony sposób odwzorowania krzywizn kół zębatych jest stosowany w modelach współpracy kół zębatych. Umożliwia on pomiar sił oraz grubości warstw smarujących.
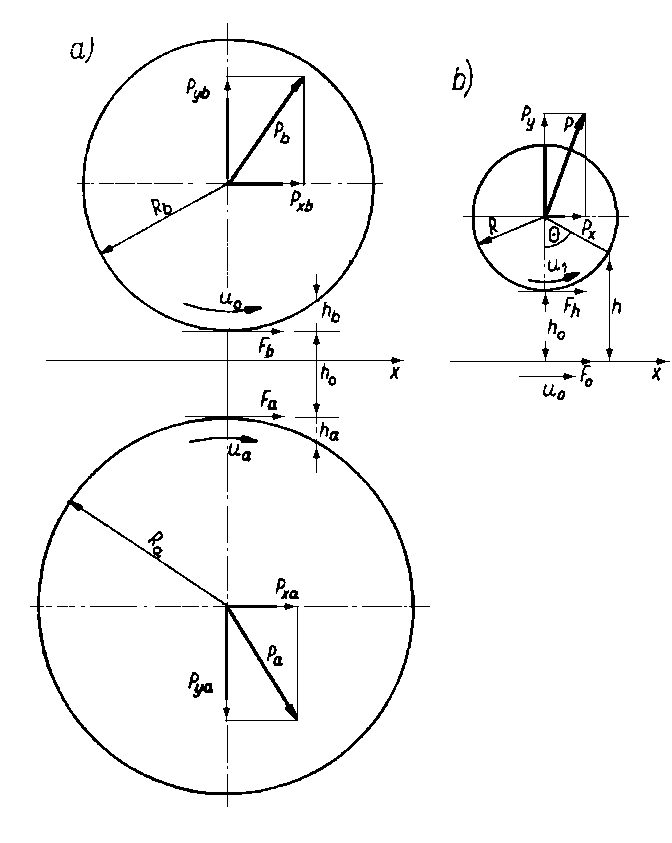 |
Rys. 6.92. Transformacja układu cylinder-cylinder
(a) na układ cylinder-płaszczyzna
(b) Fa, Fb, Fh, Fo siły styczne
|
Styk między dwoma cylindrami (rys. 6.92) można wystarczająco opisać przez równoważny styk cylindra z płaszczyzną. W tym celu musi być ustalona odpowiednia odległość między odwzorowywanymi cylindrami oraz odległość między równoważnym cylindrem a płaszczyzną. Muszą one być jednakowe dla tych samych wartości x. Konfiguracja cylinder-płaszczyzna czyni zadość temu warunkowi przy małych wartościach x. Ograniczenie to nie podważa słuszności analizy, ponieważ przy zjawiskach elastohydrodynamicznych x nie osiąga dużych wartości.
Z rys. 6.92 wynikają następujące zależności
|
h = h0 + ha + hb
| (6.329a)
|
|
h ≈ h0 + |
x²
2Ra |
+ |
x²
2Rb |
= h0 + |
x²
2 |
( |
1
Ra |
+ |
1
Rb |
)
| (6.329b)
|
Dla cylindra równoważnego (rys. 6.92)
Stąd odległość między odwzorowywanymi cylindrami będzie równa odległości między cylindrem a płaszczyzną dla każdej wartości x, jeżeli
Promień cylindra równoważnego jest więc równy
Jeżeli środki obydwu cylindrów leżą po tej samej stronie wspólnej stycznej przechodzącej przez punkt styku oraz jeżeli Ra > Rb to promień cylindra równoważnego wynosi
Składowe normalne sił Pa, Pb, P przedstawione na rys. 6.92a, b, wynikają ze wzoru
|
Pya = Pyb = Py = | ∫ | p dx
| (6.334)
|
6.10.3.Smarowanie hydrodynamiczne obszaru styku kontaktowego
Przedstawienie styku kontaktowego rzeczywistych elementów maszyn jako styku dwóch cylindrów oraz przekształcenie konfiguracji cylinder-cylinder w układ cylinder-płaszczyzna pozwala na zastosowanie teorii hydrodynamicznej.
Rozwiązanie zagadnienia dotyczącego smarowania tego skojarzenia, z wykorzystaniem podstawienia Sommerfelda, umożliwia wyznaczenie względnej grubości warstwy cieczy odniesionej do promienia cylindra
Układ współrzędnych oraz oznaczenia zachowano zgodnie z rys. 6.92b. Równanie wyprowadzono przy założeniu idealnej sztywności, a więc nieodkształcalności układu, oraz stałej lepkości.
W przypadku smarowania kół zębatych typowe wartości lepkości, prędkości i obciążenia w środku przyporu zazębienia są następujące
|
η = 0,075 Pa•s | ; |
U1 = U2 = 5 m/s | ; |
U = ½(U1 + U2) = 5 m/s | ; |
Py = 2500 kN/m .
| (6.336)
|
Względna grubość warstwy cieczy smarującej wynosi przy tych założeniach
|
h0
R |
= 0,67 •10 -6
| (6.337)
|
Zakładając wartość R = 20 mm, jako wartość promienia zastępczego cylindra odwzorowującego styk zębów koła zębatego, otrzymuje się z zależności (6.337) grubość warstwy cieczy przewidywanej dla tego przypadku przez klasyczną teorię hydrodynamiczną
ho = 0,013 µm.
Grubość warstwy cieczy jest znikomo mała nawet w stosunku do wysokości nierówności powierzchni o największych gładkościach. Praktycznie nie można potwierdzić tego wniosku. Oznacza to, że klasyczna teoria hydrodynamiczna nie może być wykorzystywana do oceny zachowania się substancji smarującej koła zębate.
Podobne rozumowanie można przeprowadzić dla łożyska tocznego. Rozważane łożysko wałeczkowe ma następujące parametry: prędkość obrotowa wału n = 5000 obr/min, średnica bieżni pierścienia wewnętrznego R1 = 32 mm, średnica wałeczka r = 8 mm, obciążenie jednostkowe wałeczka p = 300 kN/m, lepkość cieczy smarującej η = 0,01 Pa • s.
Promień zastępczego cylindra R przy tych założeniach wynosi
|
R |
= |
Ra Rb
Ra + Rb |
= |
3,2 • 0,8
3,2 + 0,8 |
= 0,64 cm
| (6.338)
|
Prędkość U można obliczyć na podstawie analizy kinematyki łożyska tocznego z następującej zależności
Wynosi ona dla tego przypadku U = 10,4 m/s.
Względna grubość warstwy smarującej wyraża się przy tych założeniach zależnością
skąd dla danego promienia R
ho = 0,010 µm.
Obliczona grubość warstwy smarującej jest zbyt mała w porównaniu z wysokością nierówności, podobnie jak w kołach zębatych, aby mogła wystarczyć do całkowitego oddzielenia współpracujących powierzchni.
6.10.4. Elastohydrodynamiczna teoria smarowania
Teoria elastohydrodynamiczna powstała jako uogólnienie klasycznej teorii hydrodynamicznej przy uwzględnieniu warunków styku kontaktowego w celu wyznaczenia rozkładu ciśnienia w strefie styku, które wpływa na właściwości cieczy smarującej i odkształcenie współpracujących elementów. Wyznacza się w tym celu kształt i grubość warstwy smarującej oraz jej nośność. Założenia, na których opiera się teoria elastohydrodynamiczna są następujące:
1) przemieszczenia są obliczane wg modelu półprzestrzeni sprężystej ciała stałego uważanego za continuum materialne;
2) pomija się istnienie upływów bocznych, co jest uzasadnione wymiarami obszaru wytwarzanego ciśnienia dynamicznego - szerokość strefy wpływu tego ciśnienia jest mała w porównaniu z długością cylindra, czyli pochodna (∂ p/∂ z) ma więc pomijalnie małą wartość;
3) warunki brzegowe są następujące: p = 0 na wlocie, w dużej odległości od strefy wysokiego ciśnienia, p = (∂ p/∂ z) = 0 na wylocie;
4) smar jest nieściśliwy;
5) pomija się zmiany lepkości i objętości cieczy smarującej spowodowane zmianami temperatury.
Przy uwzględnieniu powyższych założeń zagadnienie sprowadza się do rozwiązania układu równań
|
d
d x |
( |
h³
η |
d p
d x |
) |
= 12 U |
d h
d x |
|
η = η (p) ; | |
h = h0 + |
x²
2 R |
+ v |
| (6.341)
|
przy czym prędkość hydrodynamiczna U = ½(U1 + U2)
Suma odkształceń sprężystych dwóch stykających się ciał stałych
| |
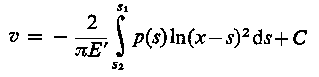
| (6.342)
|
przy czym
1
E' |
= |
1
2 |
( |
1 - ν1²
E1 |
+ |
1 - ν2²
E2 |
)
|
gdzie: E1, E2 - współczynniki sprężystości wzdłużnej stykających się materiałów (moduł Younga) w Pa, ν1, ν2 -liczba Poissona stykających się materiałów. E' - zastępczy współczynnik sprężystości wzdłużnej w Pa, s - dodatkowa współrzędna wzdłuż osi x.
Zależność lepkości od ciśnienia przedstawia równanie
gdzie: ηo - lepkość przy ciśnieniu p = 0 w Pa•s, η - lepkość przy ciśnieniu p w Pa•s, α - ciśnieniowy współczynnik (piezo współczynnik) lepkości w Pa-1
Przy tym założeniu wygodnie jest zastąpić w równaniu Reynoldsa ciśnienie p przez tzw. ciśnienie zredukowane
|
η = |
1
α |
( 1 -e -α p)
| (6.344)
|
wówczas
|
d q
d x |
= e -α p |
d p
d x
| (6.345)
|
Układ równań (6.341) tworzy tzw. izotermiczne zagadnienie smarowania elastohydrodynamicznego. Dotychczas nie znaleziono jego ogólnego rozwiązania, otrzymano natomiast wiele rozwiązań numerycznych. Główna trudność w uzyskaniu rozwiązania numerycznego polega na tym, że iteracja: ,,ciśnienie → odkształcenie → kształt warstwy oleju → ciśnienie" nie zawsze jest zbieżna.
6.10.5. Analiza wymiarowa smarowania elastohydrodynamicznego
Zmienne charakteryzujące proces smarowania elastohydrodynamicznego są następujące: zastępczy promień krzywizny R w m, zastępczy współczynnik sprężystości wzdłużnej E' w Pa, charakterystyki lepkościowe cieczy η w Pa • s, a w Pa-1, obciążenie przypadające na jednostkę długości styku W w N/m, prędkość U w m/s, grubość warstwy smaru n w m.
Ustaleniem ilości zmiennych niezależnych opisujących dane zjawisko oraz ich wymiarów zajmuje się analiza wymiarowa.
Wymiar każdej wielkości fizycznej można przedstawić jako iloraz potęg wymiarów wielkości podstawowych (długość, masa, czas). W analizie wymiarowej oznaczone one są odpowiednio jako: wymiar długości L, wymiar masy M i wymiar czasu T.
Uwzględniając podane oznaczenia można wydzielić w omawianym procesie smarowania siedem zmiennych niezależnych o następujących wymiarach:
|
q | R | E' | η0 | α | W | U
| |
L | L | M
LT | M
LT | L T²
M | M
T² | L
T
|
Charakteryzują one geometrię (h, R) kinematykę (U), dynamikę (W), materiał elementów smarowanych (E') oraz ciecz smarującą (ηo, a ).
Celem teorii smarowania elastohydrodynamicznego jest ustalenie zależności pomiędzy wyszczególnionymi powyżej zmiennymi. Zwłaszcza ważna jest relacja grubości warstwy smarującej do pozostałych zmiennych. Informacje dotyczące wpływu obciążenia i prędkości na grubość warstwy h pozwalają ocenić możliwość spełniania, założonej w procesie konstruowania, roli warstwy smarującej. Można to oszacować przez porównanie wartości h z wysokością nierówności.
Wychodząc z przytoczonych przesłanek na podstawie analizy wymiarowej można określić trzy bezwymiarowe stosunki, w funkcji których wyznacza się względną, odniesioną do promienia zastępczego, grubość warstwy smarującej
|
h
R |
= f |
( |
W
E' R' |
, |
η0 U
E' R' |
, |
α E'
)
| (6.346)
|
Zredukowanie liczby zmiennych do czterech znacznie upraszcza sposób przedstawienia zależności w porównaniu z pierwotnie rozważaną liczbą siedmiu zmiennych. Parametry bezwymiarowe w tak przyjętym układzie są zdefiniowane w następującej kolejności:
parametr grubości warstwy smarującej, parametr obciążenia, parametr prędkości i parametr materiałowy
Tablica 6.13. Charakterystyka bezwymiarowych parametrów określających proces smarowania elastohydrodynamicznego|
Parametr | Wielkości składowe | |
Ozna- czenie | wartość | obciążenie jednostkowe styku W
kN/m | promień zastępczy R
m | zastępczy moduł sprężystości E
MPa | α
1/Pa | U, m/s
przy mPa•s | |
3 | 30 | 300 | |
U | 10-13
10-12
10-11
10-10
10-9
10-8 | - | 13 | 2,3•105
stal/stal | - | 0,1
1
10
100
-
- | -
0,1
1
10
100
- | -
-
0,1
1
10
100 | |
W | 3•10-5
3•10-4 | 90
900 | 13
- | 2,3•105
stal/stal | - | - | |
G | 5000
2500
| - | - | 2,3•105
stal/stal1,15•105
brąz/brąz | 2,2•10-3 | -
| |
Powszechnie spotykane wartości parametrów W, U oraz G podano w tabl. 6.11. Najbardziej znaczący wpływ na proces smarowania ma parametr prędkości U, dlatego też w tabl. 6.11 przedstawiono szeroki zakres jego zmienności, obejmujący aż pięć rzędów wielkości, tj.: 10-8÷10-13.
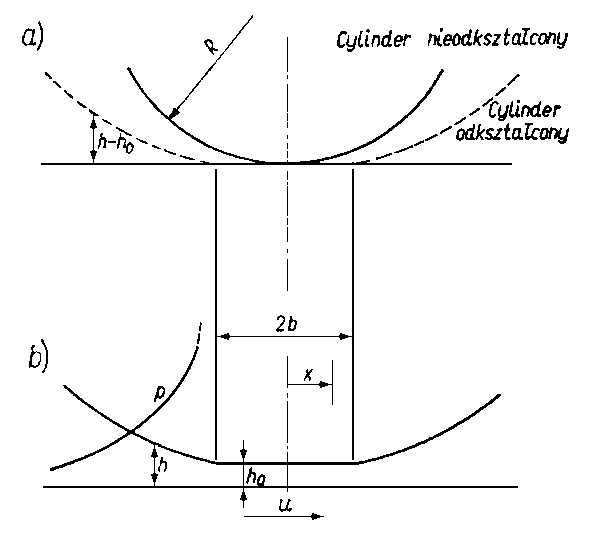 |
Rys. 6.93. Geometria styku kontaktowego:
a) powierzchnie niesmarowane,
b) powierzchnie smarowane
|
Wspomniane uprzednio prace Grubina nad smarowaniem styków kontaktowych doprowadziły do sformułowania elastohydrodynamicznej teorii smarowania. W późniejszym okresie przedstawiono wiele modyfikacji teorii elastohydrodynamicznej. Wszystkie one jednak zgadzają się w ogólnych zarysach z teorią Grubina. Najbardziej interesujące prace w tej dziedzinie przedstawili w 1961 r. Dowson i Higginson, autorzy wydanej w 1966 r. obszernej monografii smarowania elastohydrodynamicznego.
Teoria Grubina zakłada, że odkształcenie smarowanego cylindra jest takie same, jak w przypadku styku niesmarowanego. Geometrię styku sprężystego cylindra i nieodkształcalnej płaszczyzny pokazano na rys. 6.93. Z teorii sprężystości wynika następujące wyrażenie na przemieszczenie w ciele stałym na zewnątrz strefy styku Hertza (dla |x| > 0)
|
H - H0 = |
h - h0
R |
= |
4 W
π |
{
X (X² - 1)½ - ln [X + (X² - 1)½ ] }
| (6.347)
|
gdzie:
Scałkowane równanie Reynoldsa ma następującą postać
|
d p
d x |
= 12η U ( |
h - h0
h³ | )
| (6.348)
|
Wprowadzając ciśnienie zredukowane q
|
d q
d x |
= 12η0 U ( |
h - h0
h³ | )
| (6.349)
|
a następnie względne ciśnienie zredukowane
oraz korzystając z zależności określającej wymiar styku
uzyskuje się równanie Reynoldsa w postaci bezwymiarowej
|
d Q
d X |
= 48 ( |
W
2 π |
)½ |
U |
H - H0
H³
| (6.352)
|
Ciśnienie zredukowane powstające na krawędzi styku Hertza wynosi
| |
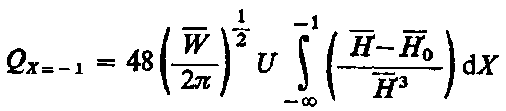
| (6.353)
|
Grubin przeprowadził całkowanie numeryczne tego wyrażenia otrzymując
|
Qx = -1 = 48 ( |
W
2 π |
)² |
U ( |
π
W |
)² |
• 0,0986 ( |
π H0
2 W |
)11/6
| (6.354)
|
Następnie Grubin oszacował lewą stronę równania (6.354) i stwierdził, że ciśnienie na krawędzi styku, tzn. przy X = - l, musi mieć wartość porównywalną z maksymalnym naciskiem Hertza. W zakresie praktycznych obciążeń oznacza to, że q ≈ (1/a ), ponieważ e - α p « l .
Z określenia Q wynika, że
|
Qx = -1 = |
q
E' |
≈ |
1
α E' |
= |
1
G
| (6.355)
|
Podstawiając oszacowaną wartość Qx = -1 do równania (3.354) oraz przekształcając je odpowiednio, otrzymuje się wartość parametru grubości warstwy smarującej
|
H0 = |
1,95 (G U)8/11
W1/11
| (6.356)
|
Pomimo prostych rozważań towarzyszących rozumowaniu Grubina, wartości grubości warstwy smarującej uzyskane z równania (6.356) są bardzo zbliżone do wartości obliczonych za pomocą innych, dokładniejszych metod oraz do wartości uzyskanych eksperymentalnie.
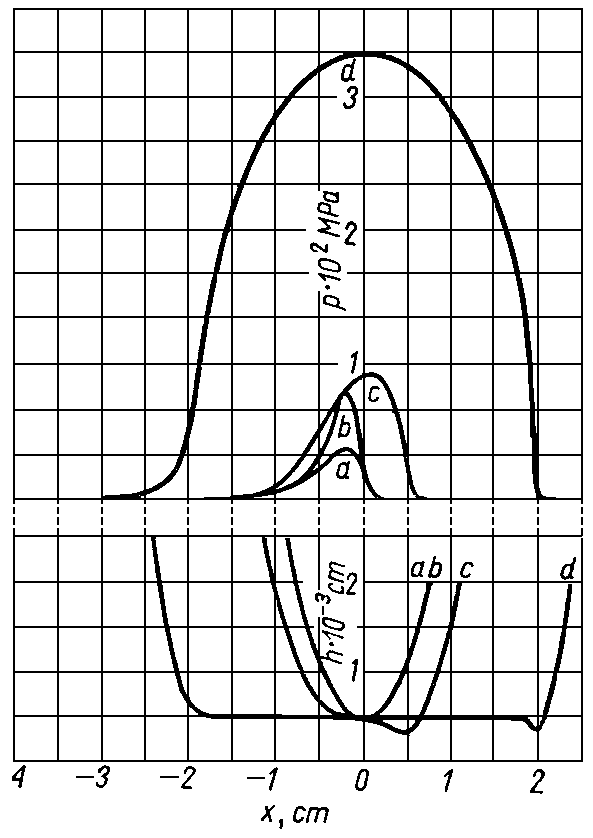 |
Rys. 6.94. Rozkład ciśnienia i kształt warstwy smarującej styku kontaktowego;
- - lepkość stała, cylindry nieodkształcalne,
- - lepkość zależna od ciśnienia, cylindry nieodkształcalne,
- - lepkość stała, cylindry sprężyste,
- - lepkość zależna od ciśnienia, cylindry sprężyste
|
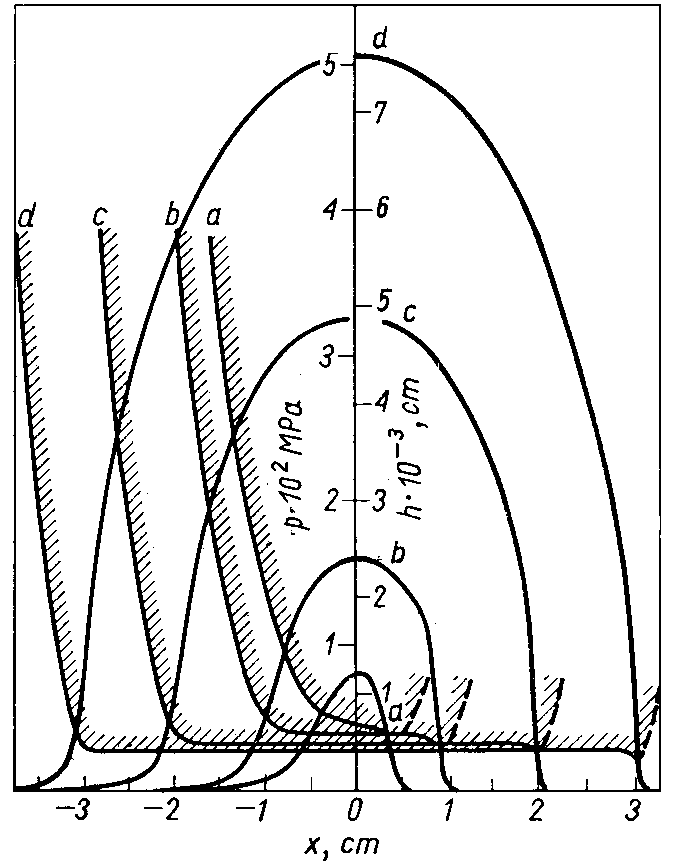 |
Rys. 6.95. Rozkład ciśnienia i kształt warstwy elastohydrodynamicznej dla różnych obciążeń zewnętrznych; objaśnienie oznaczeń patrz rys. 6.94
|
Rozwiązania zagadnienia smarowania elastohydrodynamicznego są podawane na ogół wyłącznie w postaci bezwymiarowej. Zadaniem rozwiązań jest uzyskanie zależności dotyczących wpływu obciążenia, prędkości i właściwości oleju na rozkład ciśnienia oraz grubość warstwy smarującej.
Na rys. 6.94 podano zależności charakteryzujące wpływ, jaki ma uwzględnienie oddzielnie zmian lepkości i odkształcenia sprężystego na rozkład ciśnienia i kształt warstwy smarującej. Wykresy te sporządzono przy założeniu, że grubość warstwy elastohydrodynamicznej dla x = 0 jest jednakowa we wszystkich przypadkach.
Interesującym wnioskiem z analizy krzywych przedstawionych na rys. 6.94 jest istnienie sygnalizowanego uprzednio, łącznego wpływu zmian lepkości na skutek wzrostu ciśnienia oraz sprężystości powierzchni na wielkość ciśnienia dynamicznego. Na rys. 6.95 przedstawiono zmianę kształtu krzywej ciśnienia wraz ze wzrostem obciążenia. Wyniki te uwzględniają istnienie równoczesnego wpływu zmian lepkości na skutek wzrostu ciśnienia oraz smarowanych powierzchni. Wnioski te wynikają z teorii elastohydrodynamicznej. Krzywa c na rys. 6.95 ma identyczny kształt i wartość jak krzywa J na rys. 6.94, ponieważ obydwa rysunki dotyczą tych samych warunków; E = 2,15 • 105 MPa; ν = 0,3; R = 200 cm; U = l m/s; ηo = 0,137 Pa • s. Na rys. 6.95 podano także zmianę grubości warstwy smarującej wraz ze zmianą obciążenia. Zależność tę można przedstawić w innej postaci. Na rys. 6.96 podano zmianę grubości w funkcji nacisku jednostkowego, odniesionego do
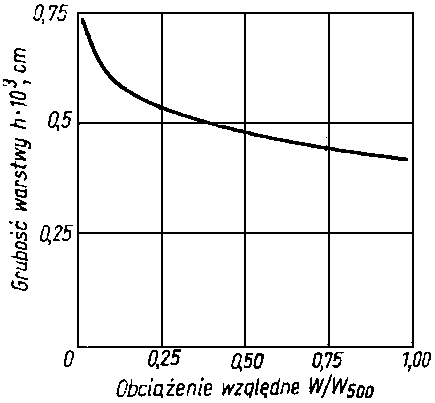 |
Rys. 6.96. Zmiana grubości warstwy elastohydrodynamicznej z obciążeniem
|
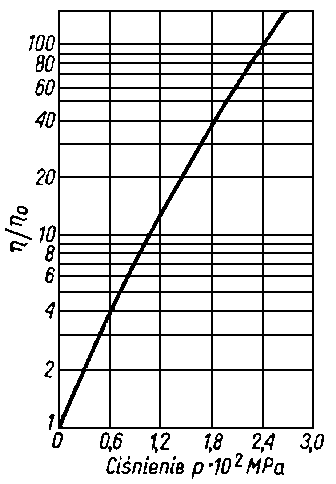 |
Rys. 6.97. Eksperymentalna zmiana lepkości oleju mineralnego η od ciśnienia względem ηo = 0,137 Pa•s
|
nacisku W500 wywołującego ciśnienie p = 500 MPa. Grubość warstwy zależy w znikomym stopniu od zmian obciążenia. Nieczułość grubości warstwy elastohydrodynamicznej na zmianę obciążenia jest jednym z najistotniejszych wniosków teorii elastohydrodynamicznej. Wszystkie trzy rys. 6.94 do 6.96 opracowano przy założeniu zmian lepkości wg zależności z rys. 6.97. Jest to typowa doświadczalna krzywa dla przeciętnego oleju mineralnego.
W celu uzyskania modelu uwzględniającego równanie gradientu ciśnienia dla oleju o lepkości zależnej od ciśnienia, z uwzględnieniem odkształceń obszarów trybologicznych, zastosowano rozwiązanie numeryczne.
Model izotermicznej warstwy oleju podczas smarowania elastohydrodynamicznego opiera się na równaniu gradientu ciśnienia i równaniu stanu. Uwzględniając wykładniczą zależność lepkości od ciśnienia można uzyskać związek między ciśnieniem rzeczywistym w warstwie elastohydrodynamicznej oleju a ciśnieniem zredukowanym, i stąd charakterystykę rozkładu ciśnienia rzeczywistego w warstwie oleju na podstawie krzywej zredukowanego ciśnienia obliczonego przy stałej lepkości. Wartość współczynnika określającego zmiany lepkości oleju w zależności od zmian ciśnienia (piezowspółczynnika) mieści się w przedziale 001 ÷ 004 m²/MN. Zatem przy małych wartościach ciśnienia, obliczanie ciśnienia rzeczywistego na podstawie ciśnienia zredukowanego nie sprawia większych trudności. Jeśli natomiast ciśnienie zredukowane ma wartość około kilkudziesięciu MN/m², to wtedy wartość ciśnienia rzeczywistego dąży do nieskończoności.
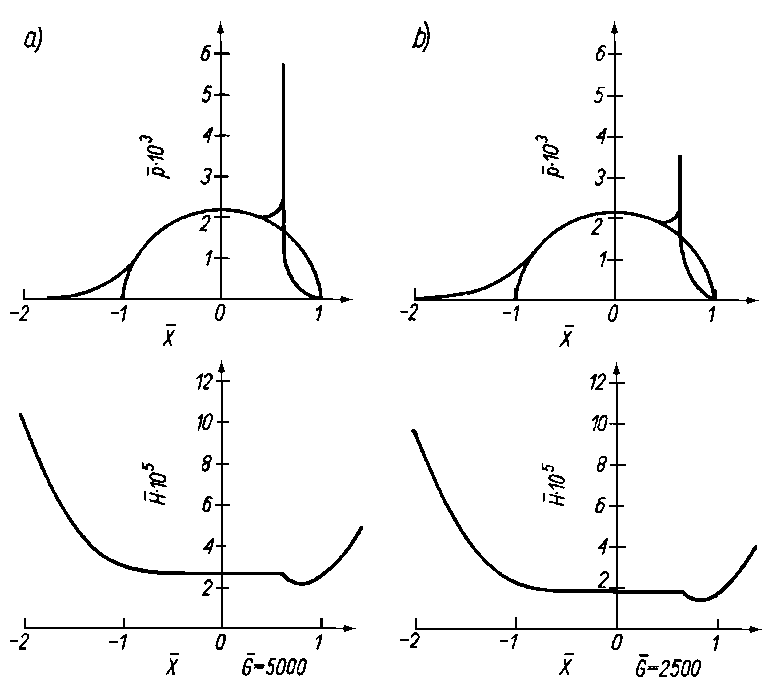 |
Rys. 6.98. Rozkład ciśnienia i kształt warstwy elastohydrodynamicznej dla różnych wartości parametrów;
- W= 3. 10 -5 - parametr obciążenia,
- U = 10 -11 - parametr prędkości,
- G - parametr materiałowy,
- H - parametr przemieszczenia w ciele stałym,
- X- parametr długości obszaru styku
|
W dalszych rozważaniach wykorzystywano wykładniczą zależność lepkości od ciśnienia, a wartości parametrów bezwymiarowych będą odpowiadały przeciętnym wartościom stosowanym w praktyce.
Na rys. 6.98 i 6.99 podano rozkłady ciśnienia wyrażonego w formie bezwymiarowej, jako p = (p/E), oraz kształty warstw elastohydrodynamicznych dla
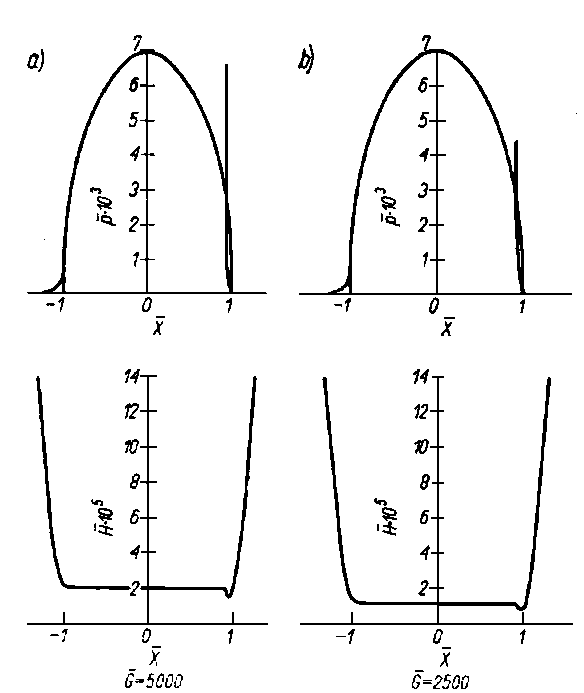 |
Rys. 6.99. Rozkład ciśnienia i kształt warstwy elastohydrodynamicznej dla różnych wartości parametru materiałowego;
- W = 3•10 -5,
- U = 10 -11,
- pozostałe oznaczenia - patrz rys. 6.98
|
różnych wartości parametrów bezwymiarowych W, U, G. We wszystkich czterech przypadkach występuje gwałtowny wzrost ciśnienia, tzw. szczyt ciśnienia po stronie wylotowej. Szczytu takiego nie obserwuje się na rys. 6.94, ponieważ wartości parametrów G i U, na podstawie których przedstawiono tam krzywe, są za małe do wytworzenia dostatecznego wzrostu ciśnienia. Z rys. 6.98 i 6.99 wynika, że wartość szczytu ciśnienia zależy przede wszystkim od wartości parametru materiałowego G, natomiast nieznacznie tylko od wartości parametru obciążenia W.
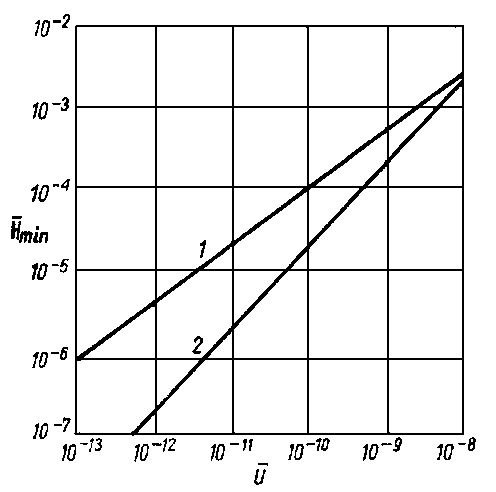 |
Rys. 6.100. Zależność grubości warstwy H smarującej od parametru U dla W =3•10 -5; G =5000;
- -teoria elastohydrodynamiczna,
- - teoria hydrodynamiczna
|
Podobnie grubość warstwy elastohydrodynamicznej wyraźnie zależy od parametru materiałowego G, natomiast w niewielkim stopniu jest zależna od parametru obciążenia W. Ponieważ jednak praktyczny zakres zmienności G jest niewielki w porównaniu z zakresem zmienności parametru prędkości U, dlatego można przyjąć, że grubość warstwy smarującej zależy głównie od parametru prędkości U. Na rys. 6.100 podano zmianę minimalnej grubości warstwy Hmin = (xmin/R) w funkcji U. Z wykresu tego wynika proporcjonalność
Dla porównania przedstawiono także grubość warstwy smarującej przewidywaną przez klasyczną teorię hydrodynamiczną.
Na rys. 6.101 podano wpływ parametru prędkości U na rozkład ciśnienia b w warstwie elastohydrodynamicznej. W miarę wzrostu wartości parametru prędkości U rozkład ciśnienia odbiega od rozkładu Hertza. Wartości szczytu ciśnienia mogą przy tym przekraczać kilkakrotnie wartość nacisku Hertza.
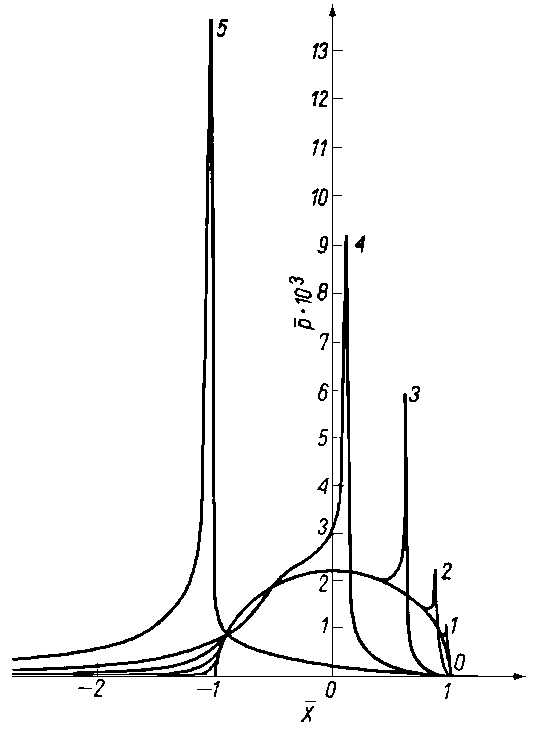 |
Rys. 6.101. Wpływ parametru prędkości U na rozkład ciśnienia w warstwie elastohydrodynamicznej przy W = 3•10 -5, G= 5000,
0 - U = 0,
1 - U = 10 -13,
2 - U = 10 -12,
3 - U = 10 -11,
4 - U = 10 -10,
5 - U = 10 -9,
|
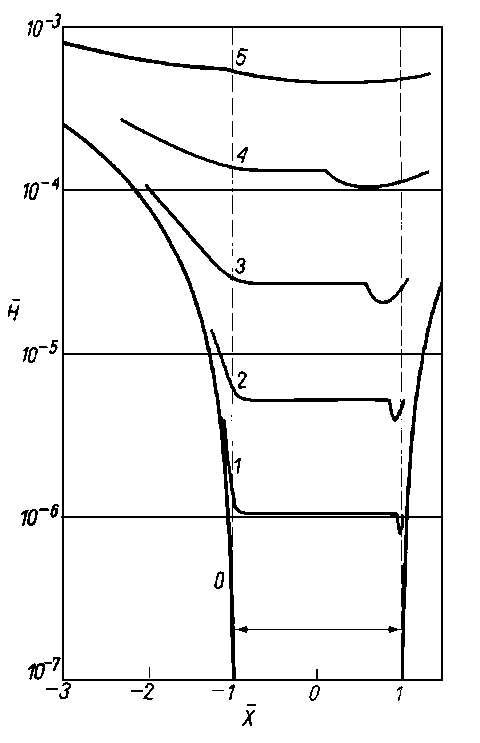 |
Rys. 6.102. Wpływ parametru prędkości U na kształt i grubość warstwy elastohydrodynamicznej, przy W = 3•10 -5, G = 5000,
0 - U = 0,
1 - U = 10 -13,
2 - U = 10 -12,
3 - U = 10 -11,
4 - U = 10 -10,
5 - U = 10 -9,
|
Na rys. 6.102 przedstawiono kształty elastohydrodynamicznej warstwy cieczy odpowiadające funkcjom ciśnienia z rys. 6.101. Obwiednie linii przedstawiających kształt warstw smarujących, dla różnych wartości parametru U (oznaczona przez 0), ograniczają obszar styku niesmarowanego, tzn. styku, jaki powstaje przy U = 0. Cechą charakterystyczną kształtu warstw elastohydrodynamicznych jest przewężenie po stronie wylotowej. Wraz ze wzrostem wartości U przewężenie to obejmuje coraz większą część strefy styku Hertza; przy najwyższej wartości U zaczyna. się ono już przed strefą styku Hertza. We wszystkich przypadkach minimalna grubość warstwy wynosi 0,7÷0,8 grubości w punkcie maksymalnego ciśnienia. Z przedstawionej analizy wynika, że parametr prędkości U jest dominującą zmienną niezależną.
Dotychczasowa analiza nie uwzględniała ściśliwości cieczy smarującej. Ciecz uznawano za idealnie nieściśliwą. Ze względu jednak na duże ciśnienia w strefie styku kontaktowego konieczne jest uwzględnienie zmian gęstości ze zmianą ciśnienia. Przy małym ciśnieniu zmiany te można uznać za liniowe. Typową eksperymentalną zależność wzrostu gęstości od ciśnienia dla oleju mineralnego przedstawiono na rys. 6.103. Zmiana gęstości na skutek wzrostu ciśnienia wpływa przede wszystkim na szczytową wartość ciśnienia.
Porównanie rys. 6.101 i 6.104 wykazuje, że we wszystkich przypadkach uwzględniających ściśliwość wartość ciśnienia szczytowego zmniejsza się i przesuwa w kierunku +x. Zmniejszenie to jest szczególnie wyraźne przy dużych wartościach parametru prędkości.
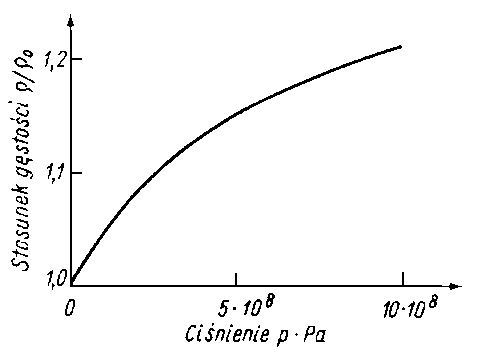 |
Rys. 6.103. Zależność gęstości od ciśnienia dla typowego oleju mineralnego
|
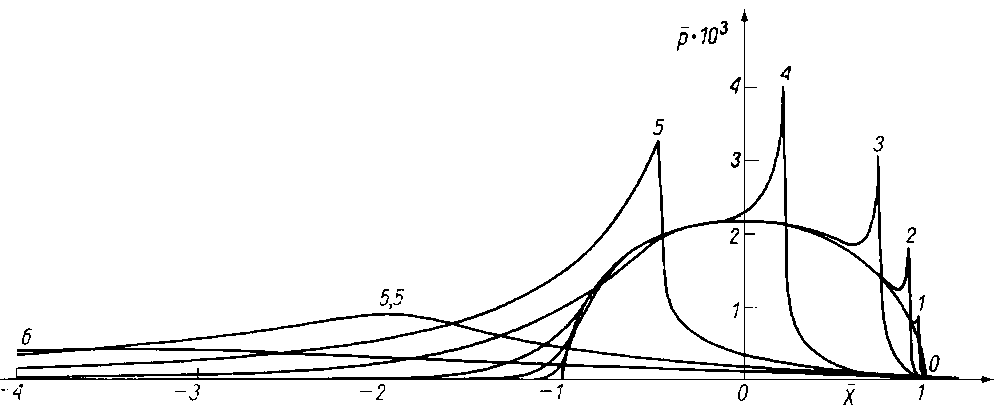 | |
Rys. 6.104. Wpływ parametru prędkości U = na rozkład ciśnienia w elastohydrodynamicznej warstwie cieczy ściśliwej, przy W = 3•10 -5, G = 5000,
0 - U = 0,
1 - U = 10 -13,
2 - U = 10 -12,
3 - U = 10 -11,
4 - U = 10 -10,
5 - U = 10 -9,
|
Uwzględnienie ściśliwości cieczy nie wpływa zasadniczo na kształt warstwy smarującej. Na rys. 6.105 przedstawiono kształt warstwy elastohydrodynamicznej dla cieczy nieściśliwej 1 oraz dla cieczy ściśliwej 2.
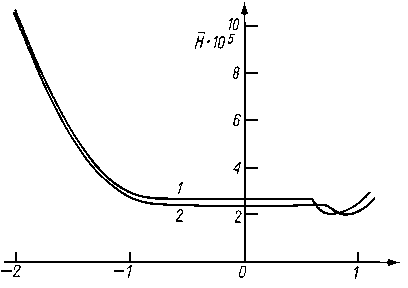 |
Rys. 6.105. Wpływ ściśliwości cieczy smarującej na kształt i grubość warstwy elastohydrodynamicznej;
l - warstwa nieściśliwa,
2 - warstwa ściśliwa
|
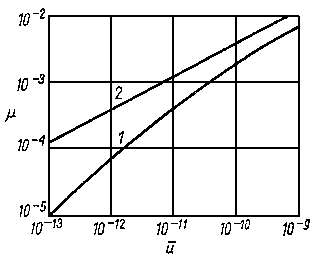 |
Rys. 6.106. Zależność współczynnika tarcia µ od parametru prędkości w obszarze styku kontaktowego przy W = 10 -5, G = 5000:
1 - teoria elastohydrodynamiczna,
2 - teoria hydrodynamiczna
|
Siła tarcia powstająca przy smarowaniu elastohydrodynamicznym jest niezależna od parametru obciążenia W i zmienia się wraz z parametrem prędkości U w taki sam sposób jak grubość warstwy. W pierwszym przybliżeniu można więc przyjąć, że siła tarcia przy czystym toczeniu jest wprost proporcjonalna do grubości warstwy smarującej. Na rys. 6.106 przedstawiono zmiany współczynnika tarcia, co przy niezależności siły tarcia od obciążenia odpowiada zmianom siły tarcia wraz z parametrem prędkości U.
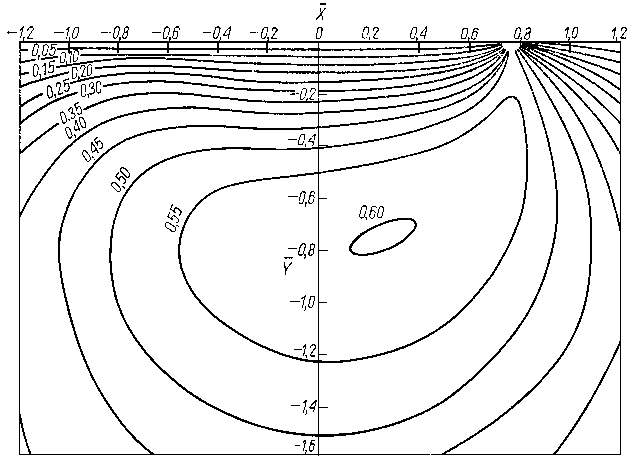 |
Rys. 6.107. Rozkład naprężeń w obszarze styku smarowanego elastohydrodynamicznie
|
Dla celów porównawczych naniesiono na nim zależność otrzymaną na podstawie klasycznej teorii hydrodynamicznej.
Rozkład naprężeń w ciele stałym powstający w warunkach smarowania styku Hertza przedstawiono na rys. 6.107. Krzywe podane na tym rysunku odpowiadają jednakowym wartościom stosunku maksymalnych naprężeń głównych do maksymalnych naprężeń Hertza. Rozkład ten dotyczy czystego toczenia, a niesymetria rozkładu naprężeń względem osi V jest wywołana istnieniem rozkładu ciśnienia dynamicznego w cieczy.
Przedstawione wyniki pozwalają określić ogólne prawidłowości smarowania elastohydrodynamicznego w sposób następujący:
1) dla danego obciążenia i prędkości toczenia, w zakresie praktycznych wartości, minimalna grubość warstwy elastohydrodynamicznej jest znacznie większa niż wynika to z klasycznej teorii hydrodynamicznej;
2) w zakresie, w którym powierzchnie odkształcają się sprężyście, grubość warstwy elastohydrodynamicznej zależy w niewielkim stopniu od obciążenia;
3) wpływ parametru materiałowego G na grubość warstwy jest tego samego rzędu, co wpływ parametru prędkości U, ponieważ zakres zmienności G jest w praktyce niewielki, dlatego U jest zmienną dominującą;
4) wraz ze wzrostem wartości parametru obciążenia W lub ze zmniejszeniem wartości parametru prędkości U, rozkład ciśnienia w cieczy przesuwa się od rozkładu hydrodynamicznego dla idealnie sztywnych cylindrów w stronę rozkładu Hertza dla suchych cylindrów;
5) dla warunków i materiałów stosowanych w praktyce występuje gwałtowny wzrost wartości ciśnienia po stronie wylotowej;
6) w przypadku czystego toczenia siła tarcia jest niezależna od parametru obciążenia W i zmienia się wraz z parametrem prędkości U w taki sam sposób, jak grubość warstwy smarującej.
Teoria smarowania elastohydrodynamicznego sformułowana przez Grubina określa w postaci bezwymiarowej przewidywaną grubość warstwy smarującej dla danych warunków współpracy stykających się materiałów. Dowson i Higginson przedstawili inną zależność, podobną jednak w ogólnych zarysach do wzoru Grubina, na grubość warstwy smarującej
|
H = |
1,6 G 0,6 U 0,7
W 0,13
| (6.358)
|
Rozbieżności między wynikami Grubina oraz Dowsona i Higginsona, co wynika z budowy wyrażeń, nie przekraczają 20%. Interesujące jest zapisanie wzoru (6.358) za pomocą wielkości mianowanych
|
h = |
1,6 α 0,6 (η0 U) 0,7 E' 0,03 R 0,043
W 0,13
| (6.359)
|
Z wyrażenia tego wynika, że grubość warstwy nieznacznie zależy od obciążenia. Wyjątkowo mały jest także inny wpływ, a mianowicie współczynnika sprężystości wzdłużnej (modułu Younga). Wykładnik 0,03 oznacza, że praktycznie grubość warstwy elastohydrodynamicznej jest niezależna od sprężystości materiału.
Ten teoretyczny wynik potwierdziły doświadczenia, w których współpracowały ze sobą szklana i stalowa tarcza. Doświadczenia te wykazały, że grubość warstwy cieczy powstającej w takim układzie jest prawie identyczna jak pomiędzy tarczami stalowymi w tych samych warunkach pracy. Oczywiście, szerokość strefy styku i rozkład ciśnień zależą w znacznym stopniu od właściwości sprężystych stykających się materiałów.
Stosowanie wzorów na grubość warstwy elastohydrodynamicznej jest ograniczone do przypadków, w których smarowane ciała są metalami, zaś ciecz smarująca podlega wykładniczej zależności lepkości od ciśnienia.
6.10.6. Elastohydrodynamiczne smarowanie przekładni zębatych
Przykładem zastosowania teorii elastohydrodynamicznej do rzeczywistych elementów maszyn może być smarowanie przekładni zębatej walcowej z zębami prostymi o zarysie ewolwentowym. Wnioski z analizy smarowania takiej przekładni przenoszą się po niewielkich modyfikacjach na inne rodzaje przekładni. Analizę tę można uznać za reprezentatywną dla większości przekładni zębatych. Uwzględnienie kinematyki i dynamiki przekładni zębatej w analizie smarowania elastohydrodynamicznego jest zagadnieniem skomplikowanym. Praca przekładni składa się z kolejno po sobie następujących cykli przyporu (zazębiania i wyzębiania). W czasie każdego z cykli następuje zmiana wartości i kierunku siły stycznej, wartości i kierunku prędkości oraz promieni krzywizny w punkcie przyporu. Dlatego teoria określona dla stanu ustalonego nie uwzględnia wszystkich czynników charakteryzujących przebieg procesu smarowania w czasie. Przyjęcie promieni krzywizny stykających się powierzchni oraz ich transformacja na dwa cylindry, a następnie na cylinder i płaszczyznę, odwzorowuje jedynie jeden wybrany punkt przyporu. Podobne ograniczenie dotyczy także prędkości i obciążenia. Z powyższych przyczyn pełna analiza powinna uwzględniać zmiany, jakim podlega warstwa elastohydrodynamiczna wzdłuż odcinka przyporu. Zgodnie z rys. 6.91 odległość pomiędzy osiami kół zębatych wynosi
gdzie R1, R2 - promienie kół zębatych.
Przełożenie przekładni wyraża się następującym wzorem
gdzie ω1, ω2 - prędkości kątowe kot zębatych.
W dalszym ciągu, dla uproszczenia rozważań matematycznych, i zawsze oznaczać będzie liczbę większą od jedności. Indeks l będzie dotyczyć zębnika (koła mniejszego), zaś indeks 2 koła większego
|
R1 = |
A
i + 1 | ; |
R2 = |
i A
i +1
| (6.362)
|
Odległość środków cylindrów równoważnych stykowi zębów jest stała i wynosi
gdzie ψ - kąt przyporu.
Oczywiście promienie krzywizny zębów w punkcie styku, a więc także promienie równoważnych cylindrów zmieniają się wzdłuż odcinka przyporu. Zgodnie z rys. 6.91 zastępczy promień krzywizny dla dowolnej odległości s od środka przyporu można więc określić następująco,
|
R = |
(R1 sin ψ + s) (R2 sin ψ - s)
(R1 + R2) sin ψ
| (6.364)
|
Prędkości toczenia walców są określone zależnościami
|
U1= |
π n1
30 |
(R1 sin ψ + s)
| (6.365a)
|
|
U2= |
π n2
30 |
(R2 sin ψ - s)
| (6.365b)
|
Prędkości te są równe prędkościom obwodowym cylindrów równoważnych, co wynika z zasady odwzorowania.
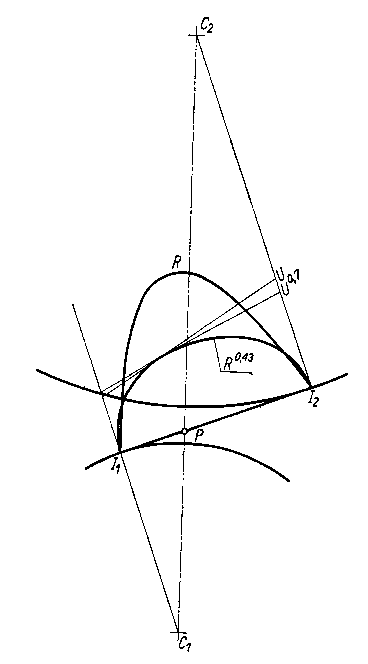 |
Rys. 6.108. Zmiana zastępczego promienia krzywizny R oraz średniej prędkości toczenia U = ½ (U1 + U2) wzdłuż odcinka przyporu
|
A więc prędkość hydrodynamiczna
|
U = ½ (U1 + U2) = |
π n1
30 |
[ R1 sin ψ - ½ (s -1) ]
| (6.366)
|
Z zależności tej wynika, że jedynie dla i = l prędkość U jest stała wzdłuż całego odcinka przyporu; dla ; i < 1 U jest funkcją chwilowego położenia punktu przyporu na linii przyporu.
Równania (6.366) i (6.367) wskazują na to, że zarówno promień cylindra zastępczego R, jak i prędkość U zależą od chwilowego położenia punktu przyporu. Jeżeli rozważania ograniczyć do określonego materiału kół zębatych (E' = idem) oraz określonej substancji smarującej (a = idem, ho = idem), to zgodnie ze wzorem (6.359) po pominięciu mało znaczącego wpływu W okaże się, że Uoraz R są jedynymi zmiennymi określającymi grubość warstwy smarującej. Charakter zmian U oraz R wzdłuż odcinka przyporu pokazano na rys. 6.108. Podano tam również przebieg występujących w równaniu (6.338) funkcji U0,7 oraz R0,43. Z wykresów tych wynika charakter zmian h wzdłuż linii przyporu. Na rys. 6.109 pokazano przykład takiej zależności dla przekładni o następujących parametrach: odległość osi kół zębatych A = 0,3 m, przełożenie przekładni i = 5.
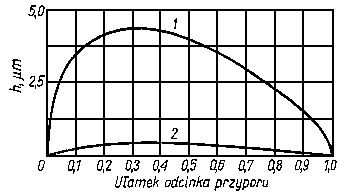 |
Rys. 6.109. Zmiana grubości h warstwy smarującej wzdłuż odcinka przyporu;
1 - teoria elastohydrodynamiczna,
2 - teoria hydrodynamiczna
|
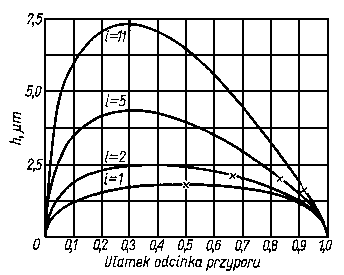 |
Rys. 6.110. Zmiana grubości h warstwy elastohydrodynamicznej wzdłuż odcinka przyporu dla przekładni o różnych położeniach
|
Na wykresie tym naniesiono dla porównania krzywą dla idealnie sztywnych zębów i oleju o stałej lepkości.
Cechą charakterystyczną rozkładu grubości warstwy elastohydrodynamicznej wzdłuż linii przyporu są większe grubości warstwy po stronie styku głowy zęba zębnika z powierzchnią zęba współpracującego oraz mniejsze grubości po stronie styku głowy zęba koła większego z powierzchnią zęba zębnika.
Na rys. 6.110 przedstawiono wpływ przełożenia przekładni na rozkład grubości warstwy smarującej wzdłuż odcinka przyporu. Grubość warstwy w środku przyporu, tzn. na kole podziałowym, w przybliżeniu jest stała, niezależnie od przełożenia. Z tego względu grubość ta jest dogodnym parametrem charakterystycznym warstw elastohydrodynamicznych powstających w różnych warunkach pracy przekładni.
Jeśli na kole podziałowym poślizg jest równy zeru, to z warunku tego wynikają następujące zależności na U oraz R
|
U = |
π n1
30 |
R1 sin ψ |
= |
π n1
30 |
i A
i + 1 |
sin ψ
| (6.367)
|
|
R = |
i A
(i + 1)² |
sin ψ
| (6.368)
|
Jeżeli
|
h = |
k (η0 U) 0,7R 0,043
W 0,13 | i |
k = 1,6 α 0,6 E' 0,03
|
to grubość warstwy elastohydrodynamicznej na kole podziałowym
|
hp = k |
(Asin ψ )1,13
W 0,13 |
( |
η0 π n1
30 |
)0,7 |
i 1,13
(i + 1)1,56
| (6.370)
|
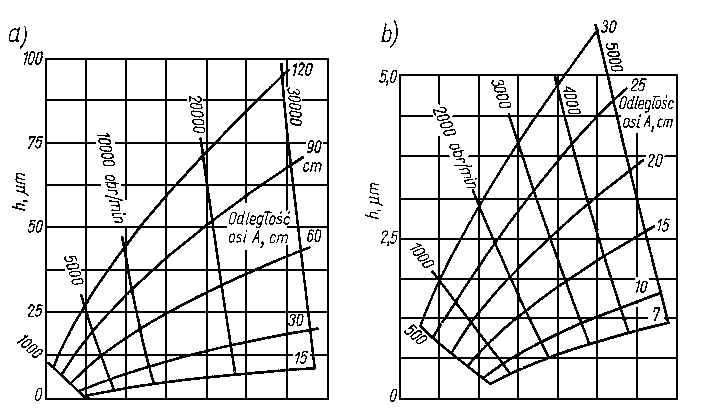
Rys. 6.111. Zależność grubości h warstwy elastohydrodynamicznej na kole podziałowym od prędkości obrotowej nwiększego koła przekładni zębatej oraz od odległości między osiami kół zębatych
|
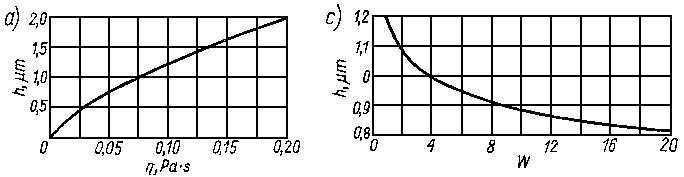 |
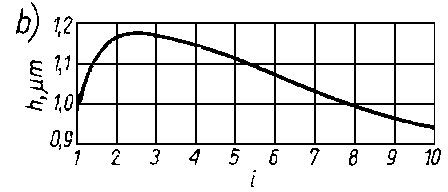 Rys. 6.112. Współczynniki korekcyjne uwzględniające wpływ:
- a) lepkości,
- b) przełożenia,
- c) obciążenia
na grubość h warstwy elastohydrodynamicznej
|
Na rys. 6.111 przedstawiono zależności grubości warstwy elastohydrodynamicznej na średnicy podziałowej od prędkości obrotowej większego koła i wielkości przekładni dla następujących parametrów: przełożenie przekładni i = l, obciążenie W = 400 kN/m, lepkość substancji smarującej η = 0,075 Pa • s.
Grubość warstwy smarującej uzyskaną z rys. 6.111 dla wyżej wymienionych wartości i, W oraz ηo można wykorzystać do wyznaczenia grubości warstwy powstającej przy innych (niż wyszczególnione powyżej) wartościach przełożenia, obciążenia i lepkości. W tym celu należy grubość warstwy wyznaczoną z rys. 6.112 pomnożyć przez odpowiednie współczynniki korekcyjne, uwzględniające wpływ lepkości, przełożenia i obciążenia. Uzyskaną w ten sposób wartość należy porównać z chropowatością powierzchni. Pozwala to ocenić efektywność, z jaką warstwa elastohydrodynamiczna oddziela od siebie współpracujące powierzchnie zębów.
|