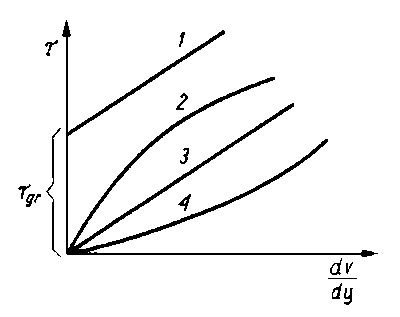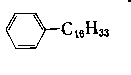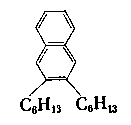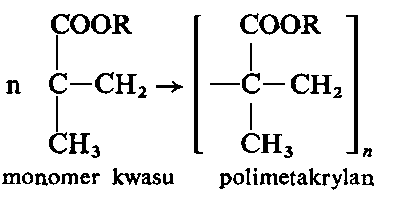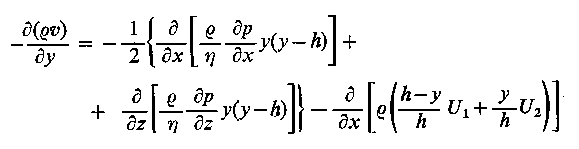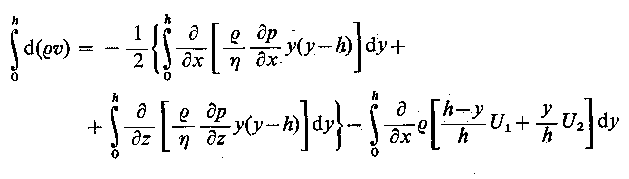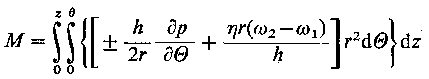Contents
Spis treści

    

6. Tarcie płynne

6.1. Smarowanie przy różnych rodzajach tarcia

Tarcie płynne występuje w obszarach styku ciał stałych, jeśli te obszary są rozdzielone warstwą substancji smarującej, a tarcie zewnętrzne zostało zastąpione tarciem wewnętrznym w tej substancji. Tarcie wewnętrzne w płynie powoduje zmniejszenie oporów tarcia zmniejszenie intensywności zużywania oraz zwiększenie tłumienia drgań. Substancja smarująca przepływająca przez obszar tarcia zwiększa intensywność odprowadzania ciepła i odprowadzania produktów zużycia oraz przeciwdziała korozji.
Grubość i charakter warstwy smarującej określają rodzaj smarowania. Kryterium podziału smarowania może być względna grubość warstwy smarującej, definiowana następująco:
R = grubość warstwy smarującej
średnie odchylenia od linii środkowej nierówności współpracujących powierzchni		 = h
Ra1 + Ra2 		(6.1)

Rodzaje smarowania elementów maszyn sklasyfikowane wg wartości kryterium R podano na rys. 6.1.
Smarowanie przy tarciu granicznym R < l. Opory tarcia i zużywanie powierzchni współpracujących w warunkach tarcia granicznego zależą od własności powierzchni oraz od aktywności powierzchniowej substancji smarnej. Lepkość cieczy ma znikomy wpływ na warunki tarcia granicznego (rys. 6.2). Grubość powstającej
Rys. 6.1. Rodzaje smarowania elementów maszyn

    Rys. 6.2. Model tworzenia warstwy smarującej przy tarciu granicznym;
  1. warstwa podłoża,
  2. warstwa tlenków lub związków ochronnych,
  3. smarowanie, graniczne

na powierzchni ciała stałego warstwy izolującej jest mała w porównaniu z chropowatością powierzchni.

Smarowanie przy tarciu płynnym 5 < R < 100. Całkowite wyeliminowanie zużycia elementów maszyn na skutek tarcia, można uzyskać przez stosowanie smarowania płynnego. Wytwarzana pomiędzy współpracującymi powierzchniami warstwa cieczy lub gazu oddziela je całkowicie, eliminując oddziaływanie nierówności

Rys. 6.3. Model warstwy przy smarowaniu płynnym:
a) uproszczony model warstwy powstającej podczas smarowania płynnego,
b) porównanie warstwy oddzielającej powierzchnie podczas smarowania płynnego i elastohydrodynamicznego;
  1. - warstwa ochronna lub graniczna,
  2. - ciecz smarna,
  3. - ciało sprężyste,
  4. - ciało stałe*
* - ciało stałe o pomijalnym odkształceniu w zakresie stosowanych obciążeń.

(rys. 6.3). Ciśnienie w tej warstwie wytwarza się na skutek względnego ruchu powierzchni (smarowanie hydrodynamiczne i gazodynamiczne) lub też zewnętrznego źródła zasilającego (smarowanie gazostatyczne i hydrostatyczne).

Grubość warstwy wielokrotnie przewyższa grubość warstwy granicznej i sumaryczną chropowatość obu powierzchni. Płyn (ciecz lub gaz) ma własności pozwalające stosować klasyczne prawa przepływu lepkiego. Lepkość substancji smarującej jest więc najważniejszą cechą charakteryzującą tarcie płynne. Na przebieg tarcia płynnego wpływa także gęstość stosowanego płynu. Zwłaszcza ważna jest ona wtedy, gdy czynnikiem smarującym jest gaz, a więc przy smarowaniu gazostatycznym i gazodynamicznym.
Przyjmuje się, że dla całkowitego oddzielenia nierówności powierzchni, grubość warstwy powinna co najmniej pięciokrotnie przewyższać sumę wartości Ra, czopa i panewki (Ra1 + Ra2 ). Spotykane powszechnie substancje smarujące uniemożliwiają uzyskanie grubości warstwy większej niż h = 100(Ra1 + Ra2 ), dlatego też ograniczono smarowanie hydrodynamiczne do zakresu 5 ≤ R ≤ 100.
Smarowanie przy tarciu elastohydrodynamicznym l ≤ R ≤ 10. Klasyczna teoria hydrodynamiczna, która opisuje tarcie płynne, nie uwzględnia odkształceń sprężystych powierzchni. Odkształcenia takie należy uwzględnić w warunkach działania dużych obciążeń na zakrzywione powierzchnie.
Powstająca pomiędzy takimi powierzchniami warstwa jest nazywana warstwą elastohydrodynamiczną. Na skutek działania dużych obciążeń wzrasta lokalnie (w strefie styku) lepkość cieczy tworzącej warstwę elastohydrodynamiczną. Uwzględnienie obydwu wymienionych czynników, a więc odkształceń sprężystych powierzchni i zmiany lepkości ze wzrostem ciśnienia, pozwala zastosować teorię hydrodynamiczną do łożysk tocznych, przekładni zębatych oraz krzywek.
Smarowanie przy tarciu mieszanym R ≤ 5. W większości spotykanych elementów maszyn występuje jednocześnie tarcie graniczne, płynne i elastohydrodynamiczne. Występuje także często zjawisko powstawania mikroklinów związanych z oddziaływaniem pojedynczych nierówności, dodatkowo podwyższające obciążalność warstwy. Zespół tych zjawisk występujących równocześnie nazywa się tarciem mieszanym (rys. 6.4).
    Rys. 6.4. Model warstwy przy tarciu mieszanym;
  1. - warstwa graniczna,
  2. - ciecz, smarna

Rozważania dotyczące tarcia mieszanego muszą zatem uwzględniać zarówno fizyczne własności cieczy (lepkość, gęstość, ściśliwość itp.), jak i jej własności fizykochemiczne (zdolność do adsorpcji i chemisorpcji, powinowactwo chemiczne dodatków względem powierzchni) oraz własności fizyczne i chemiczne elementów trących.
Grubość warstwy oleju powstającej w warunkach tarcia mieszanego przewyższa na ogół dwa do pięciu razy sumę (Ra1 + Ra2 ). Rodzaj tarcia zależy głównie od jakości substancji smarującej, prędkości i obciążenia obszarów tarcia. Własności substancji smarującej charakteryzują głównie jej własności reologiczne.
    

6.2. Własności Reologiczne ciekłych substancji smarnych

6.2.1. Ciecze newtonowskie i nienewtonowskie

Zasadniczą różnicą pomiędzy trzema podstawowymi stanami skupienia materii: gazowym, ciekłym i stałym są wzajemne odległości między cząsteczkami, określające wartość sił spójności (kohezji).
W cieczach odległości międzycząsteczkowe są małe. Cząsteczki podlegają znacznym siłom przyciągania i mogą swobodnie przesuwać się względem siebie. Przemieszczanie poszczególnych cząstek lub warstw cząstek ciała względem siebie napotyka na opór sił spójności. Im większe siły spójności, tym większe są opory tarcia wewnętrznego ciała (rys. 6.5).

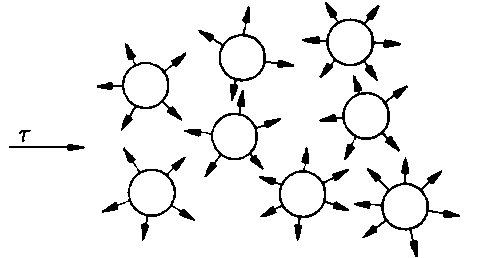
Rys. 6.5. Oddziaływanie międzycząsteczkowe w cieczy powodujące opory tarcia

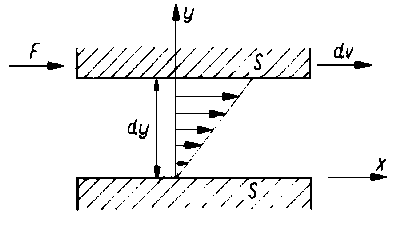
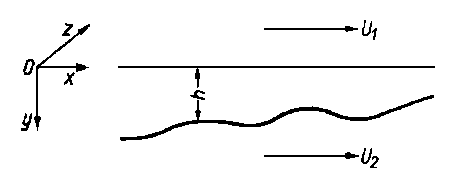
Rys. 6.6. Ruch cieczy między dwiema płytkami

Przepływ można określić jako proces ścinania cieczy. Jeżeli odkształcenie spowodowane przez ścinanie oznaczymy przez g, to prędkość ścinania
vśc d y
d t 		(6.2)

gdzie t = czas w s.

Prędkość ścinania charakteryzująca powstawanie odkształceń w czasie jest funkcją naprężenia stycznego t
vśc = f( t ) (6.3)

Jest to najogólniejsze równanie reologiczne¹.

Na rys. 6.6 przedstawiono warstewkę cieczy znajdującą się między dwiema równoległymi płytkami o powierzchni S. Dolna płytka jest nieruchoma, natomiast górna może się przesuwać względem płytki dolnej. Do niej przykładamy stycznie siłę F powodującą ruch cieczy. Naprężenie ścinające t wywołujące ruch cieczy jest określone wzorem
t = F
S 		(6.4)

Jeżeli naprężenie ścinające t jest proporcjonalne do gradientu prędkości cieczy, wówczas ogólne równanie reologiczne przybiera postać równania Newtona
t = h d v
d y		 lub F = h S d v
d y 		(6.5)

¹ Reologia jest nauką o płynięciu i deformacji wszystkich form materii pod wpływem naprężeń.

Współczynnik proporcjonalności h jest nazywany dynamiczną lepkością newtonowską. Liczbowo jest on równy sile stycznej działającej na jednostkę powierzchni warstewek cieczy, które znajdują się w jednostkowej od siebie odległości i poruszają się względem siebie z prędkością różniącą się o jednostkę. Współczynnik h wtedy jest równy jedności, gdy siła jednego niutona przypadająca na l m² powierzchni cieczy spowoduje różnice prędkości l m/s między dwiema warstewkami cieczy odległymi od siebie o l m.
Ciecze stosujące się do równania Newtona są nazywane cieczami newtonowskimi. Prędkość ścinania vśc w cieczach newtonowskich jest równoznaczna z gradientem prędkości warstewki cieczy
vśc = d v
d y 		(6.6)

a więc charakteryzuje rozkład prędkości w warstwie cieczy. Dla cieczy newtonowskiej lepkość jest tylko funkcją temperatury i ciśnienia, a nie zależy od prędkości ścinania.
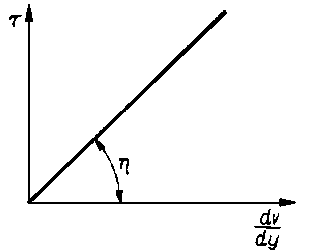
    Rys. 6.7. Krzywe płynięcia cieczy newtonowskich;
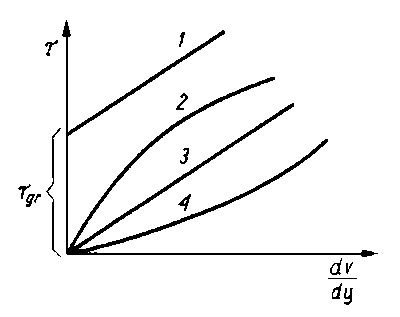
    Rys. 6.8. Linia płynięcia cieczy nienewtonowskiej
  1. - ciecz binghamowska,
  2. - ciecz pseudoplastyczna,
  3. - ciecz newtonowska,
  4. - ciecz dylatacyjna

Krzywą płynięcia cieczy newtonowskiej jest linia prosta (rys. 6.7). Ciecze o małej i średniej masie cząsteczkowej oraz roztwory substancji o małej masie cząsteczkowej są cieczami newtonowskimi.

Ciecze nienewtonowskie są to ciecze, których krzywe płynięcia nie są liniami prostymi. Ich lepkość często jest nazywana lepkością pozorną lub strukturalną.
Przedstawiony podział cieczy na newtonowskie i nienewtonowskie ma charakter umowny, gdyż każda ciecz newtonowska zachowuje się w określonych warunkach (temperatury, ciśnienia, prędkości ścinania itp.) jak ciecz nienewtonowska.
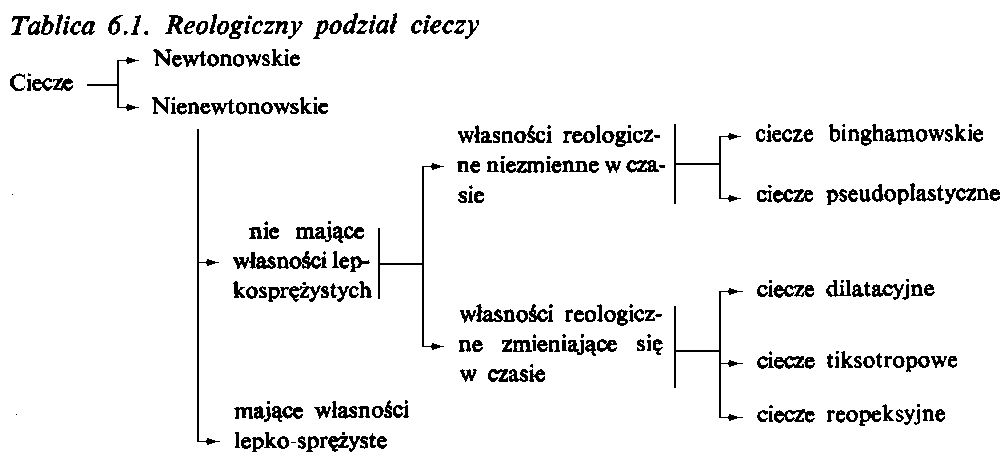
Ciecze nienewtonowskie można podzielić na trzy zasadnicze grupy (tabl. 6.1):
  • ciecze, których własności reologiczne nie zmieniają się w czasie (prędkość ścinania jest funkcją naprężenia ścinającego; charakter krzywych płynięcia tej grupy cieczy przedstawiono na rys. 6.8);
  • ciecze, których własności reologiczne zmieniają się w czasie (prędkość ścinania jest funkcją naprężenia ścinającego i czasu);
  • ciecze lepkosprężyste, wykazujące oprócz własności lepkościowych i efekty sprężyste.
Ciecz binghamowska (ciecz Binghama, ciecz plastyczna) - ciecz, która zaczyna płynąć dopiero wówczas, gdy naprężenie styczne t między dwiema warstewkami cieczy przekroczy pewną wartość graniczną tgr.
Przykładem takiej cieczy mogą być różnego rodzaju pasty, zawiesiny itp. Po przekroczeniu tgr struktura wewnętrzna ulega zniszczeniu i ciecz zachowuje się jak ciecz newtonowska. Z chwilą gdy naprężenie styczne zmniejszy się poniżej tgr to struktura wewnętrzna zostaje odbudowana.
Ciecz pseudoplastyczna - nie ma granicy płynięcia, lepkość pozorna maleje ze wzrostem prędkości ścinania. Ciecze takie mają zazwyczaj niesymetrycznie zbudowane cząstki (np. o wydłużonym kształcie liniowym). W miarę zwiększania prędkości ścinania cząstki te przyjmują uporządkowane ułożenie, wskutek czego zmniejszają się opory tarcia, a więc i lepkość pozorna.
Ciecz dylatacyjna - nie ma granicy płynności. Lepkość pozorna rośnie w miarę wzrostu prędkości ścinania (przykładem może być mokry piasek).
Podczas szybkiego ścinania zawiesiny, ciecz spełniająca rolę smaru między cząstkami zawiesiny zostaje wyparta i opory ścinania rosną.

Ciecze o własnościach reologicznych zmieniających się w czasie

Ciecz tiksotropowa - pod wpływem ścinania następuje rozpad struktury wewnętrznej. Im dłuższy czas działa naprężenie ścinające, tym większe następuje zniszczenie struktury. Pozostawienie cieczy tiksotropowej w spokoju powoduje odbudowę struktury wewnętrznej. Typowym przykładem cieczy tiksotropowej są smary plastyczne, których lepkość pozorna zmniejsza się, gdy poddamy je oddziaływaniom mechanicznym. Ciecz tiksotropowa można uważać za taką ciecz pseudoplastyczna, której uporządkowanie cząsteczek podczas przepływu zachodzi w czasie.
Ciecze reopeksyjne - pod wpływem ścinania następuje tworzenie struktury wewnętrznej. Z cieczami takimi spotykamy się w praktyce bardzo rzadko.
Ciecze lepkosprężyste. Do tej grupy cieczy należą ciecze o bardzo dużej lepkości, a równocześnie wykazujące pewne własności sprężyste. Przykładem takiego rodzaju cieczy mogą być różnego rodzaju żywice, smoły, asfalty, niektóre polimery itp. Ciecz lepkosprężysta jako bardzo lepka ciecz zachowuje się zgodnie z prawem Newtona, a ze względu na własności sprężyste - również z prawem Hooke'a.

6.2.2. Jednostki lepkości

Opierając się na wzorze Newtona można lepkość określić następującym wzorem
h = F
S		 d y
d v 		(6.7)

Jednostką lepkości dynamicznej, określoną na podstawie powyższego wzoru za pomocą jednostek układu CGS, jest l puaz (l P). Ciecz ma lepkość jednego puaza wówczas, gdy dwie warstewki cieczy o powierzchni l cm², oddalone od siebie o l cm, pod działaniem siły l dyny poruszają się z prędkością l cm/s.

W układzie CGS jednostkę lepkości dynamicznej określa się więc z zależności
[
g • cm
cm²		 • s
cm²
 ]
1 P = [ dyna • s
cm²		 ] = = [ g
cm • s		 ] (6.8)

W układzie SI jednostką lepkości dynamicznej jest paskalosekunda
1 Pa • s = [ N • s
m²		 ] = [ kg
m •s		 ] (6.9)

Ponieważ paskalosekunda Pa • s jest jednostką dużą, dlatego też w praktyce używa się jednostki 1000 razy mniejszej zwanej milipaskalosekundą mPa- s
1 mPa • s = 1 cP
Odwrotność lepkości dynamicznej h nazywa się płynnością F
F = 1
h		 [ cm • s
g		 ] = [ 10 m • s
kg		 ] (6.10)

W obliczeniach hydrodynamicznych posługujemy się najczęściej lepkością kinematyczną
n = h
r 		(6.11)

gdzie q - gęstość cieczy.

Jednostką lepkości kinematycznej w układzie CGS jest l stokes (St).
Ciecz ma lepkość l St, jeżeli jej gęstość jest równa l g/cm³ i do wzajemnego przesunięcia z prędkością l cm/s dwóch jej warstw o powierzchni l cm² odległych od siebie o l cm trzeba użyć siły l dyny
1 St = [
dyna
cm²		 • s
g
cm³ 		] = [ cm²
s		 ] = [ 10-4 m²
s		 ] (6.12)

Częściej używane są jednostki mniejsze, centistokesy (cSt) i milistokesy (mSt).
W układzie SI wymiarem lepkości kinematycznej jest: m²/s = 104 • St = 106 cSt (l cSt = 1 mm ²/s). Lepkość wyrażona w jednostkach układu CGS lub SI nazywa się lepkością bezwzględną.
Dla celów praktycznych, gdy chodzi tylko o porównanie cieczy posługujemy się pojęciem lepkości względnej lub lepkości umownej.
Lepkość względna może być liczbą bezwymiarową, gdy np.: porównuje się lepkość dynamiczną danej cieczy z lepkością dynamiczną cieczy wzorcowej, np. wody:
hwzgl = hc
hw 		(6.13)

gdzie: hc - lepkość dynamiczna cieczy w temperaturze tc w Pa • s, hw - lepkość dynamiczna cieczy wzorcowej (wody) w temperaturze tw w Pa • s.

Jeżeli lepkość względna jest wyrażona jako stosunek lepkości dynamicznej cieczy do lepkości dynamicznej wody w temperaturze 20,2°C, to wtedy liczbowo równa się lepkości dynamicznej danej cieczy wyrażonej w mPa • s, gdyż w temperaturze 20,2°C lepkość dynamiczna wody jest równa l mPa • s.
Najczęściej jednak lepkość wyraża się w jednostkach umownych, które stanowią zwykle stosunek czasu wypływu badanej cieczy do czasu wypływu cieczy wzorcowej w ściśle znormalizowanych warunkach pomiaru lub po prostu określają czas wypływu badanej cieczy ze znormalizowanego aparatu w znormalizowanych warunkach.
W Polsce i w większości krajów europejskich, lepkość względną określa się za pomocą stopni Englera (°E). Lepkość w stopniach °E jest to stosunek czasu wypływu 200 cm³ badanej cieczy w danej temperaturze do czasu wypływu tej samej ilości wody destylowanej w temperaturze 20°C przez znormalizowaną kapilarę aparatu Englera.
W Wielkiej Brytanii i USA określa się lepkość względną za pomocą sekund Redwooda. Jest to czas wypływu 50 cm³ badanej cieczy w sekundach. Ponieważ istnieją dwa rodzaje lepkościomierzy Redwooda, rozróżnia się dwa rodzaje sekund Redwooda (sekundy Redwooda handlowe i sekundy Redwooda Admirality). We Francji stosowane są stopnie Barbe (°B), które określają ile cm³ cieczy wypłynie w ciągu godziny z lepkościomierza Barbego.
W USA powszechnie stosowane jest wyrażenie lepkości za pomocą sekund Saybolta określających czas wypływu 60 cm³ badanej cieczy z lepkościomierza Saybolta.
Ponieważ lepkościomierz ma 2 wymienne kapilary, z których jedną stosuje się dla cieczy o małej lepkości, a drugą dla cieczy o dużej lepkości, rozróżnia
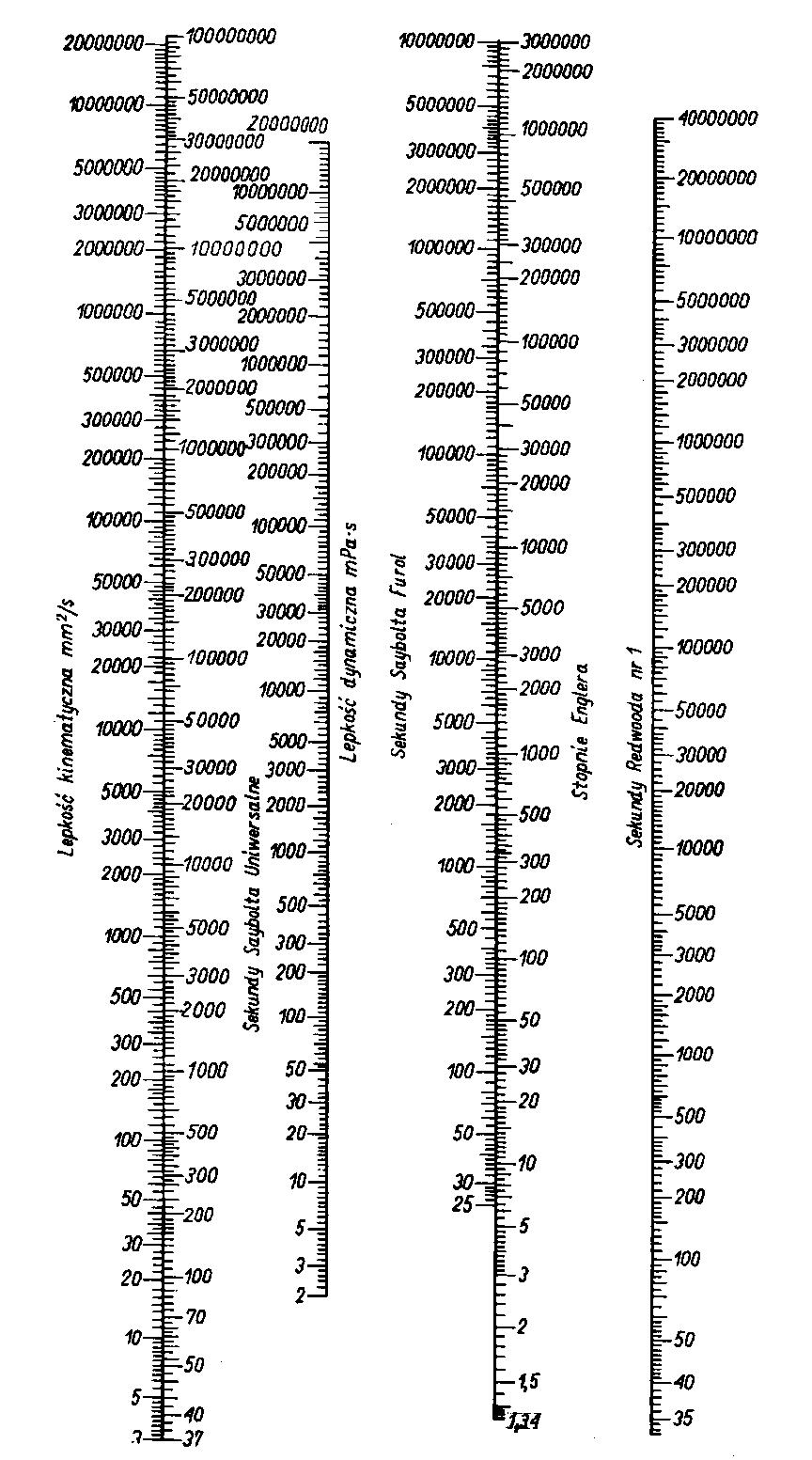Rys. 6.9. Nomogram do przeliczania jednostek lepkości

Tablica 6.2. Przeliczanie jednostek lepkości

Lepkość ki-
nematyczna
mm²/s		Lepkość względnaw stopniach
Englera
(°E)
w sekundach Saybolta
Uniwersalnych (S.U.S)
w temperaturze		w sekundach Redwooda
(handlowe)
w temperaturze
37,8°
(100°F)		54,4°C
(130°F)		98,9°C
(210°F)		21,1°C
(70°F)		60°C
(140°F)		93,3°C
(200°F)
232,032,732,830,231,031,21,140
336,036,136,332,733,433,71,224
439,139,239,435,335,936,31,308
542,342,442,637,938,538,91,400
645,545,645,840,541,141,51,481
748,748,849,043,243,744,11,563
852,052,152,446,046,346,91,653
955,455,555,848,949,149,71,746
1058,858,959,251,752,052,61,837
1162,362,462,754,855,055,61,928
1265,966,066,457,958,158,72,020
1369,669,770,161,061,361,92,120
1473,473,573,964,464,665,22,219
1577,277,377,767,767,968,72,323
1681,181,381,771,071,472,22,434
1785,185,385,774,774,975,82,540
1889,289,489,878,178,579,42,644
1993,393,594,081,782,183,12,755
2097,597,798,285,485,886,92,870
21101,7101,9102,489,289,590,72,984
22106,0106,2106,792,993,394,53,10
23110,3110,5111,196,797,198,33,22
24114,6114,8115,4100,4100,9102,23,34
25118,9119,1119,7104,2104,7106,13,46
26123,3123,5124,2108,1108,6110,03,58
27127,7127,9128,6111,9112,5114,03,70
28132,1132,4133,0115,8116,5118,03,82
29136,5136,8137,5119,7120,4122,03,95
30140,9141,2141,9123,7124,4126,04,07
31145,3145,6146,3127,5128,3130,14,20
32149,7150,0150,8131,5132,3134,14,32
33154,2154,5155,3135,4136,3138,14,45
34158,7159,0159,8139,3140,2142,24,57
35163,2163,5164,3143,3144,2146,24,70
36167,7168,0168,9147,2148,2150,34,83
37172,2172,5173,4151,2152,2154,24,96
38176,7177,0177,9155,2156,2158,35,08
39181,2181,5182,5159,2160,3162,55,21
40185,7186,0187,0163,2164,3166,75,34
Uwaga:
Wartość lepkości kinematycznej nie zależy od temperatury w jakiej została wyznaczona (tak np. 10 mm²/s jest zawsze 10 mm²/s), lepkość względna natomiast zwłaszcza ta, która jest równa czasowi wypływu cieczy z aparatu, zależy nieznacznie od temperatury pomiaru (rozszerzalność cieplna aparatu, dyszy wypływowej itp.). Dla lepkości względnej w °E błędy wynikające z różnic temperatury są zmniejszone w znacznym stopniu przez odnoszenie czasu wypływu oleju do czasu wypływu wody.

się dwa rodzaje sekund Saybolta. Saybolt Uniwersal Seconds i Saybolt Furol Seconds (SUS i SFS). W celu przeliczenia jednostek umownych na jednostki bezwzględne stosowane są różnego rodzaju zależności przedstawione za pomocą empirycznych wzorów lub nomogramów.

Wykres na rys. 6.9 jest stosowany do przeliczania poszczególnych rodzajów jednostek umownych na jednostki bezwzględne.
Nomogramy i podane wzory przeliczeniowe mają jedynie charakter mniej lub więcej przybliżony i gdy chodzi o dużą dokładność w określeniu lepkości, należy ją określać bezpośrednio w jednostkach bezwzględnych (tabl. 4.2).

6.2.3. Pomiary lepkości

Ciecz przeciwstawia się przesuwaniu jej warstewek względem siebie zarówno przy ruchu cieczy względem dowolnego ciała znajdującego się w tej cieczy, jak i ruchu tego ciała względem cieczy. Obydwa przypadki wykorzystane są do mierzenia lepkości. W celu dokładnego wyznaczenia lepkości cieczy przy jej ruchu, ruch ten powinien być ruchem warstwowym, a przynajmniej jak najbardziej zbliżonym do tego rodzaju ruchu. Ruch taki odbywa się jedynie przy małych prędkościach w przewodach o bardzo małej średnicy (zwanych kapilarami).
Pomiar lepkości, wykorzystujący przepływ cieczy przez kapilary, opiera się na prawie Hagena-Poiseuille'a
h = pr4Dp t
8 l V 		(6.14)
gdzie: r - promień kapilary w cm, l - długość kapilary w cm, t - czas płynięcia w s, Dp - różnica ciśnień powodująca przepływ cieczy w Pa, V - objętość cieczy przepływającej w czasie t w cm³.

Jeżeli ciecz przepływa przez kapilarę tylko pod działaniem własnego ciężaru, wówczas różnicę ciśnienia Dp wyraża się wzorem
p = h1 - h2
2 		r g (6.15)

gdzie: h1 - h2 - różnica poziomów cieczy w cm, r -gęstość cieczy w g/cm³, g - przyspieszenie grawitacyjne w cm/s².

Zatem wzór (6.14) przybierze postać
h = pr4 ( h1 - h2 ) g
16 l V 		r t (6.16)

Jeżeli przyjmie się
pr4 ( h1 - h2 ) g
16 l V 		= K (6.17)

to w rezultacie otrzyma się wzór o prostszej postaci
h = K t r (6.18)
gdzie K - stała kapilary niezależna od temperatury.

Dzieląc obie strony równania przez r otrzymuje się wzór na lepkość kinematyczną
n = K t (6.19)

Tak więc w metodach opartych na przepływie cieczy przez kapilary, wystarcza przy pomiarze lepkości kinematycznej wyznaczyć jedynie czas przepływu cieczy przez kapilarę.

Spośród najbardziej rozpowszechnionych lepkościomierzy (wiskozymetrów) przepływowych należy wymienić lepkościomierze: Ostwalda, Ostwalda-Pinkiewicza, Vogel-0ssaga i Ubbelohde'a (rys. 6.10). Służą one do oznaczania lepkości kinematycznej dla celów eksploatacyjnych oraz naukowo-badawczych.
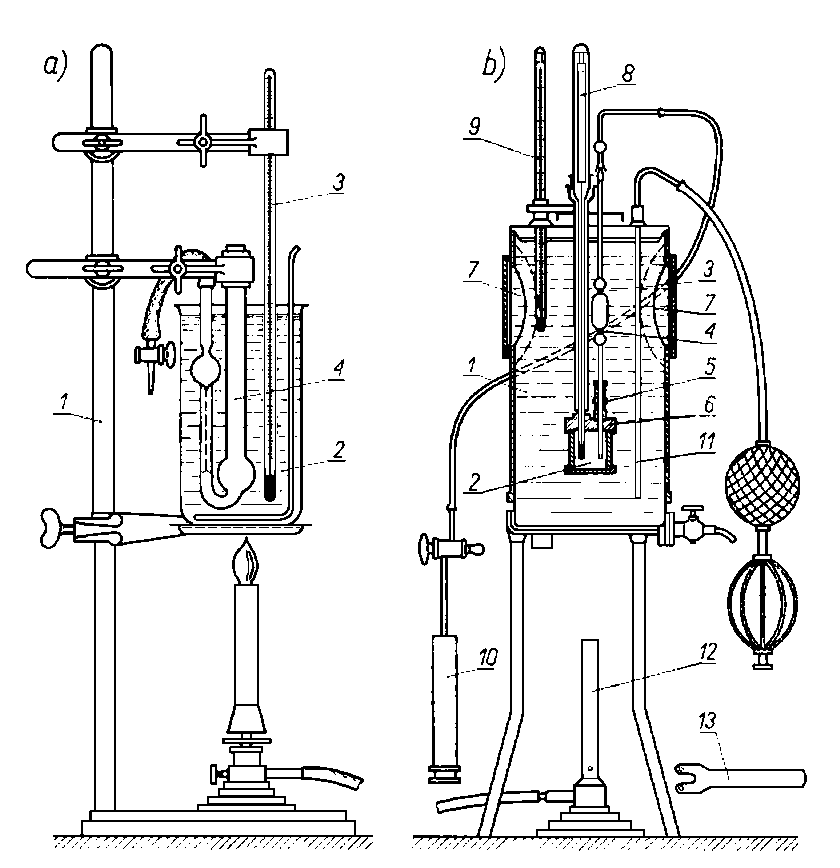    Rys. 6.10. Lepkościomierze kapilarne:
  1. lepkościomierz Ostwalda-Pinkiewicza;
  1. lepkościomierz Vogel-0ssaga;
    1. - statyw,
    2. - łaźnia,
    3. - termometr,
    4. - lepkościomierz;
    1. - termostat,
    2. - zbiorniczek oleju,
    3. - kreski na kapilarze,
    4. - kreski na kapilarze,
    5. - oprawka z gwintem,
    6. - pokrywka,
    7. - wzierniki,
    1. - termometr oleju,
    2. - termometr termostatu,
    3. - pompka olejowa,
    4. - mieszadło powietrza,
    5. - palnik gazowy,
    6. - klucz do przykręcania kapilary

W przypadku ruchu ciał stałych w ośrodkach ciekłych w grę wchodzi jedynie tarcie wewnętrzne między warstewkami cieczy, ponieważ na powierzchni ciała stałego jest zaadsorbowana warstewka cieczy.
Do obliczania lepkości stosuje się wiele wzorów uwzględniających zarówno charakter ruchu i kształt poruszającego się ciała.
Przy opadaniu ciał kulistych stosuje się prawo Stokesa. Pomiar lepkości opartej na tej metodzie polega na zmierzeniu czasu opadania kulki o znanych wymiarach i gęstości, w badanym ośrodku ciekłym. Jeżeli kulka porusza się ze stałą prędkością w ośrodku ciekłym, to opór na skutek wewnętrznego tarcia cieczy można wg Stokesa wyrazić równaniem
P = 6 p r h v (6.20)
gdzie: r - promień kuli w m, h - lepkość dynamiczna w Pa•s, v - prędkość opadania kulki w m/s.

Na kulkę opadającą w cieczy wypełniającej naczynie działają trzy siły: ciężar kulki Pk, wypór cieczy równy ciężarowi wypartej przez kulkę cieczy Pc i siła tarcia wewnętrznego cieczy P. Ciężar kulki Pk i wypór cieczy Pk wyraża się analogicznymi wzorami
Pk = 4
3		 p r ³ r k g (6.21)
Pc = 4
3		 p r ³ r c g (6.22)

gdzie: g - przyspieszenie grawitacyjne w m/s², rc, rk -gęstość cieczy i gęstość materiału kulki w kg/m³.

Ze wzoru Stokesa wynika, że opór cieczy przeciwdziałający ruchowi kulki jest proporcjonalny do prędkości kulki. Po osiągnięciu przez kulkę odpowiedniej prędkości opór ten zrównoważy pozorny ciężar kulki. Od tej chwili ruch kulki będzie jednostajny
P = Pk - Pc (6.23)

Po podstawieniu ze wzorów (6.20) do (6.22) odpowiednich wartości na P, Pk i Pc otrzymuje się
6 p r h v = 4
3		 p r ³ ( r k - r c ) g (6.24)

a stąd
h = 2 r ² ( r k - r c ) g
9 v 		(6.25)
gdzie v - prędkość opadania kulki.

Podstawiając z kolei
v = l
t		 i 2 r ² g
9 l		 = K (6.26)

otrzymamy
h = 2 r ² ( r k - r c ) g t
9 l 		(6.27)

lub
h = K ( r k - r c ) t (6.28)

gdzie: l - droga przebyta przez kulkę w m, t - czas opadania kulki w s, K - wielkość stała dla danego przyrządu.

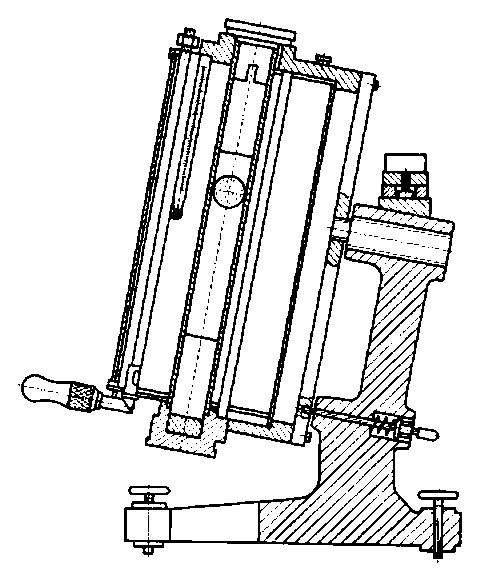
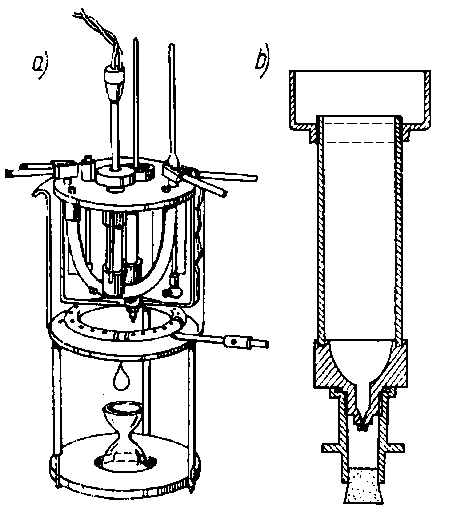
    Rys. 6.11. Lepkościomierz Höplera
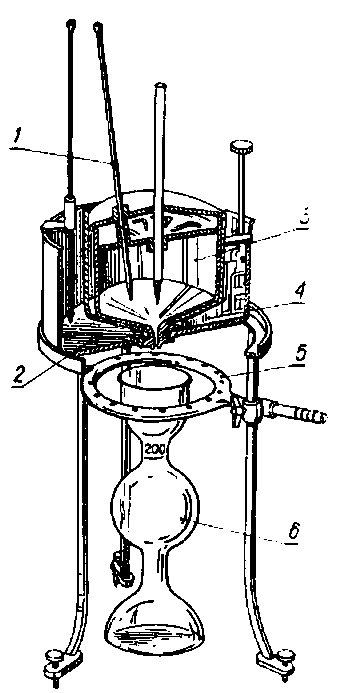
    Rys. 6.12. Lepkościomierz Englera:
  1. - termometr,
  2. - łaźnia wodna,
  3. - naczynie pomiarowe,
  4. - mieszadło,
  5. - palnik gazowy,
  6. - kolba

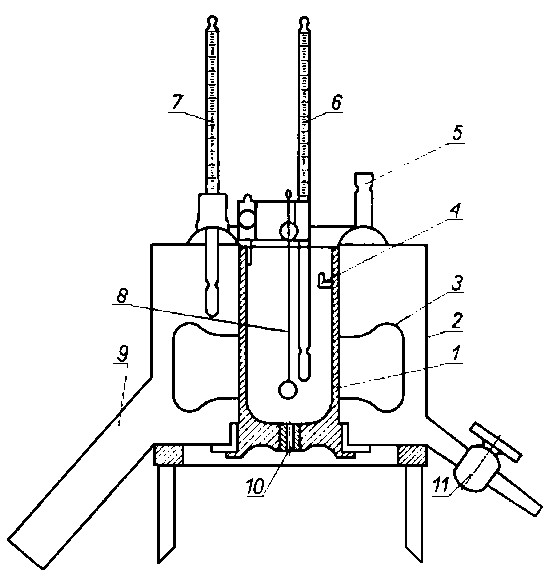    Rys. 6.13. Lepkościomierz Saybolta:
  1. widok ogólny,
  2. naczynie pomiarowe
    Rys. 6.14. Lepkościomierz Redwooda;
  1. - naczynie na olej,
  2. - łaźnia grzejna,
  3. - mieszadło,
  4. - wskaźnik poziomu,
  5. - wlew,
  6. - termometr oleju,
  7. - termometr do łaźni,
  8. - zatyczka,
  9. - rękaw grzejny,
  10. - otwór wypływowy,
  11. - kurek spustowy

Praktycznie więc pomiar sprowadza się do zmierzenia czasu opadania odpowiednio dobranej kulki oraz na wyznaczeniu gęstości badanej cieczy.
Najbardziej rozpowszechnionym typem lepkościomierzy opartym na tej metodzie jest lepkościomierz Höplera (rys. 6.11).
Dla celów technicznych, zwłaszcza w przemyśle naftowym, opracowano wiele lepkościomierzy do szybkich i łatwych pomiarów lepkości względnej.
Lepkościomierze tego typu odznaczają się dużą trwałością i prostą obsługą. Pomiar lepkości jest oparty na wyznaczeniu czasu wypływu badanej cieczy przez kalibrowany otwór z naczynia o określonej pojemności (rys. 6.12, 6.13 i 6.14).
Wszystkie typy lepkościomierzy mają łaźnie pozwalające utrzymywać stałą temperaturę podczas pomiaru. Istnieją jeszcze inne sposoby pomiarów lepkości olejów rzadziej stosowane, oparte na zanikaniu wahań ciała stałego w badanej cieczy, na tłumieniu drgań skrętnych tarczy zanurzonej w badanej cieczy, na zasadzie pomiaru oporu stawianego cieczy obracającemu się w niej walcowi itp. Do pomiarów cieczy o konsystencji półstałej (lepkość 105 - 1014 mPa) służą konsystometry (najczęściej Höplera rys. 6.15). Pomiar polega na oznaczeniu czasu i drogi, którą przebędzie kulka odpowiednio obciążona i zanurzona w badanej substancji o określonej temperaturze.
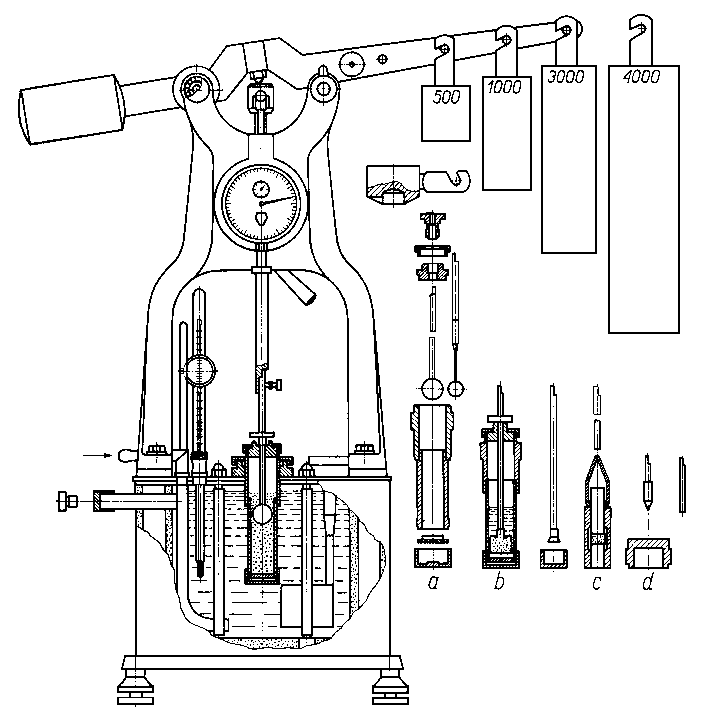    Rys. 6.15. Konsystometr Höplera:
  1. urządzenie do wyznaczania lepkości normalnej,
  2. urządzenie do wyznaczania lepkości strukturalnej,
  3. urządzenie do wyznaczania modułu elastyczności,
  4. urządzenie do wyznaczania twardości

Przyrządy te umożliwiają również wyznaczanie granicznych naprężeń ścinających w przypadku układów koloidalnych.

6.2.4. Zależność lepkości od ciśnienia

Wywarcie na ciecz ciśnienia powoduje zbliżenie jej cząsteczek do siebie i zwiększenie oddziaływań międzycząsteczkowych powodujące zwiększenie lepkości. Wpływ ciśnienia na lepkość przedstawiono schematycznie na rys. 6.16. Małe ciśnienie powoduje nieznaczny wzrost lepkości, przy większym ciśnieniu przyrost ten jest znaczny.
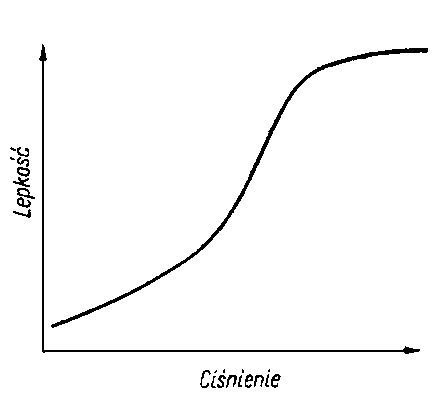Rys. 6.16. Zależność lepkości od ciśnienia

Przy ciśnieniach rzędu kilku tysięcy MPa zaznacza się już wpływ odpychania międzycząsteczkowego i krzywa przyrostu lepkości ze wzrostem ciśnienia staje się bardziej płaska, zbliżając się asymptotycznie do pewnej stałej wartości.

Rozpatrywanie zależności lepkości od ciśnienia nie jest zagadnieniem wyłącznie teoretycznym, lecz ma duże znaczenie praktyczne. W skojarzeniach trących maszyn bardzo często występują ciśnienia rzędu kilku tysięcy MPa. W przekładniach zębatych naciski w obszarach zazębienia osiągają wartość kilkuset, a nawet kilku tysięcy MPa. Najczęściej przyjmuje się, że do około 25 MPa zależność ta ma charakter liniowy i do obliczenia zmian lepkości w tych zakresach można się posłużyć wzorem
hp = ho ( 1 + a p ) (6.29)
gdzie: hp - lepkość dynamiczna przy ciśnieniu p w Pa • s, ho - lepkość dynamiczna przy ciśnieniu atmosferycznym w Pa • s, a - stała dla danego oleju.

Dla ciśnień powyżej 25 MPa zaznacza się bardzo znaczny przyrost lepkości i stosuje się wzory uwzględniające wykładniczą zależność lepkości od ciśnienia
hp = ho ap (6.30)

lub wzór Barusa
hp = ho ea p (6.31)
gdzie: a - stała (dla olejów mineralnych rzędu 1,002-1,004, dla olejów roślinnych i zwierzęcych rzędu 1,001-1,0015, gdy p jest w kG/cm² ), a - ciśnieniowy współczynnik lepkości w 1/Pa.

Ostatni wzór jest najczęściej stosowany w rozważaniach teoretycznych. Ze względu na duże znaczenie praktyczne zależności lepkości od ciśnienia, przeprowadzono w różnych ośrodkach szczegółowe badania dla olejów z ropy naftowej i różnych cieczy stosowanych do smarowania maszyn. W roku 1953 ukazało się na ten temat obszerne sprawozdanie Amerykańskiego Stowarzyszenia Inżynierów Mechaników - ASME (13). Badania prowadzono aż do zakresu ciśnień 980,665 • 106 Pa w temperaturze 0°C. 25°C, 37,7°C, 99°C, 218°C. Okazało się, że wzór wykładniczy daje dobre rezultaty tylko w zakresie umiarkowanych ciśnień, natomiast przy wysokich ciśnieniach wartości lepkości olejów obliczone z wzoru wykładniczego i zmierzone, różnią się 500 razy. Znaczne różnice występują również w różnych zakresach
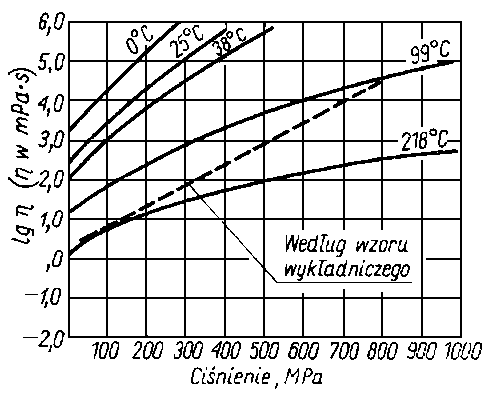Rys. 6.17. Zależność lepkości od ciśnienia dla oleju 32G (krzywe wyznaczone eksperymentalnie i krzywa obliczona)

temperatury, czego wzór wykładniczy nie uwzględnia (rys. 6.17). Różnice te uwydatniają się zwłaszcza w przypadku olejów o charakterze parafinowym.

Hersey i Hopkins (24) wykonali dla ASME studium problemu zależności lepkości od ciśnienia ze sprawozdaniem z wyników badań oraz pełnym bardzo szczegółowym opracowaniem literatury. Obszerne badania nad zależnością lepkości od ciśnienia przeprowadzono w Laboratorium Ciśnieniowym Instytutu Naftowego w Hanowerze (Institut für Erdolforschung) przez Kussa (27). Kuss zmodyfikował równanie wykładnicze wprowadzając wzór
hp = ho e( a p + b p² ) (6.32)
gdzie: hp,  ho - jak we wzorze (6.29), a, b   współczynniki mające różne wartości dla różnych olejów (a   w 1/Pa, b   w 1/Pa²).

F. Hotte (17) sprawdził przydatności istniejących wzorów i rozrzut błędów, jakie powstają przy obliczeniach w stosunku do pomiarów dla 413 substancji (147 czystych substancji, 68 olejów syntetycznych i 198 olejów z ropy naftowej).
Wzór na zależność lepkości od ciśnienia opracował również Blok
lg hp
ho		 = B lg ( 1 + p
b		 ) (6.33)
gdzie: b, B stale dla danego oleju przy określonej temperaturze.

Roelands podał trzy wzory na zależność lepkości od ciśnienia
lg hp
ho		 = K1p
1 + c1p 		(6.34)

lg hp
ho		 = K2 pc2 (6.35)

lg hp = ( lg ho +1,2) • (1 + p
2000		 )z (6.36)
gdzie: K1, c1, K2, c2, z - stałe dla danego oleju przy określonej temperaturze.

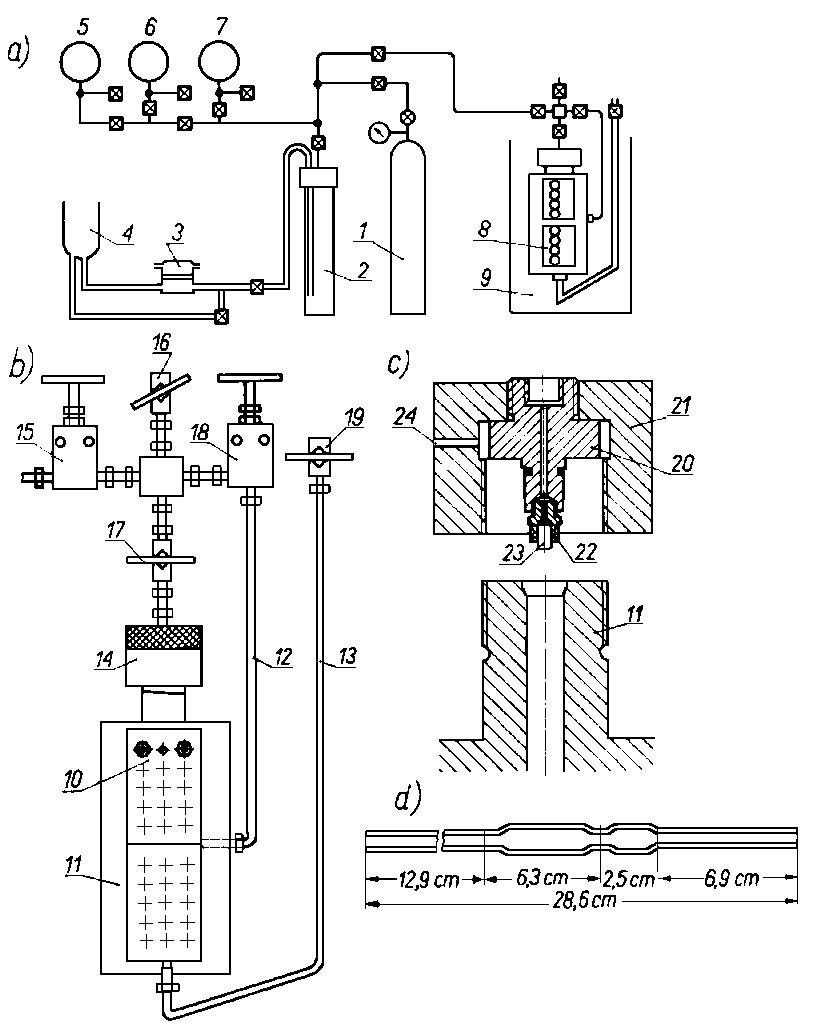Rys. 6.18. Urządzenie do pomiaru lepkości przy wysokim ciśnieniu:
a) schemat urządzenia pomiarowego;
1 - zasilająca butla gazowa,
2 - pojemnik manipulacyjny,
3 - pompa oleju,
4- zbiornik oleju,
5 do 7 - zawory wysokociśnieniowe,
8 - lepkościomierz ciśnieniowy,
9 - łaźnia do utrzymania stałej temperatury;
 b) lepkościomierz ciśnieniowy;
10-okienka wziernikowe,
11 - pojemnik ciśnieniowy,
12 - przewód wyrównawczy,
13 - przewód napełniania,
14 - głowica zamykająca,
15 do 19 - zawory ciśnieniowe;
 c) głowica zamykająca (14);
20 - wewnętrzna głowiczka ciśnieniowa,
21 - zdejmowana przykrywka,
22 - uchwyt kapilarny,
23 - kapilara,
24-zawór bezpieczeństwa;
d) kapilara (23)

Wielu autorów, jak Witt (16), Roelands, Noack (25) opracowało wzory uwzględniające równocześnie zależność lepkości od ciśnienia i temperatury. Ma to szczególnie duże znaczenie przy określeniu zachowania się oleju w węzłach tarcia. Bardzo wnikliwe badania nad zależnością lepkości od ciśnienia przeprowadził Cameron (7). Stwierdził on, że wzór wykładniczy Barusa (6.31) może scharakteryzować zależność od ciśnienia tylko dla olejów o charakterze naftenowym (punkt anilinowy poniżej 90°C). Współczynnik ciśnieniowy lepkości a można obliczyć z zależności
a = ( 0,6 + 0,9565 lg ho ) • 10-8 1/Pa (6.37)
gdzie ho - lepkość dynamiczna przy ciśnieniu atmosferycznym w mPa • s.

Dla olejów o charakterze parafinowym (punkt anilinowy powyżej 90°C) Cameron ustalił następującą zależność
(lg hp )3/2 = m ( p + b ) (6.38)

przy czym stałą m można obliczyć ze wzoru
m = (1,3 +7,1 lg ho ) • 10-2 (6.39)

a stałą b z zależności (lg ho)3/ = m b, a dla lepkości ho powyżej 6 mPa • s wystarczająco dokładna jest zależność:
m = 0,076 lg ho (6.40)

gdzie: ho - w mPa • s, p - w tysiącach funtów/cal² (funt/cal² = 6,896 • 10³ Pa), b - w cal²/1000 funtów.

Lepkość przy wysokich ciśnieniach wyznacza się w ciśnieniowych kapilarnych lepkościomierzach (rys. 6.18). Przy pomiarach lepkości pod ciśnieniem rzędu kilku tysięcy MPa Cameron stosował metodę optyczną (prążki interferencyjne).

6.2.5. Zależność lepkości od temperatury

6.2.5. l. Zmienność lepkości cieczy wraz ze zmianami temperatury

Lepkość cieczy wraz ze wzrostem temperatury maleje, natomiast lepkość gazów rośnie. Obniżenie temperatury powoduje odwrotny skutek. Wyjaśnienia tego zjawiska należy szukać w charakterze ruchu poszczególnych cząsteczek oraz działających na nie sił. Im wyższa jest temperatura, tym większa jest energia kinetyczna cząsteczek i tym większe prawdopodobieństwo wystąpienia bezładnych zderzeń cząsteczek, co powoduje zwiększenie lepkości, czyli oporów tarcia wewnętrznego.
Przy podwyższaniu temperatury wzrasta jednocześnie odległość między poszczególnymi cząsteczkami. Jest to równoznaczne ze zmniejszeniem wzajemnego oddziaływania, a więc zmniejszeniem lepkości. Jeżeli cząsteczki występują w ośrodku blisko siebie, jak w cieczach, zasadniczą rolę w zmianach lepkości spełnia oddalenie cząsteczek od siebie. W miarę większego oddalania cząsteczek, oddziaływanie między nimi maleje szybko do zera i wtedy dominujący wpływ na lepkość ma ruch cieplny. Obserwuje się to w gazach, których lepkość wzrasta z podwyższeniem temperatury.
Jak widać z powyższego rozważania, na zmianę lepkości cieczy wraz ze zmianami temperatury ma wpływ przede wszystkim wzajemne oddziaływanie cząsteczek. Ogólnie rzecz biorąc im cząsteczki cieczy są większe i im bliżej siebie, tym ciecz ma większą lepkość. Tym też tłumaczy się wpływ ciśnienia na lepkość (zmniejszenie odległości cząsteczek) oraz wpływ ilości i wielkości cząsteczek, a więc wpływ asocjacji na lepkość.
Dotychczas nie udało się ustalić ogólnej zależności między lepkością a masą cząsteczkową cieczy oraz zmienności lepkości wraz ze zmianami temperatury.

6.2.5.2. Zmienności lepkości olejów wraz ze zmianami temperatury

Oleje smarne podobnie jak inne ciecze zmieniają swoją lepkość wraz ze zmianą temperatury. Zjawisko to może powodować groźne w skutkach konsekwencje podczas eksploatacji urządzeń ze względu na zaburzenia w procesie smarowania. Zmniejszenie lepkości oleju, a więc zmniejszenie oporów tarcia wewnętrznego, ułatwia wyciskanie oleju spomiędzy trących elementów maszyn. Może to doprowadzić do zatarcia, a więc zniszczenia urządzenia. Wzrost lepkości przy obniżaniu temperatury eksploatacji powoduje wzrost strat na pokonywanie tarcia wewnętrznego cieczy. Może to doprowadzić również do trudności w uruchamianiu maszyny lub też to uruchomienie uniemożliwić.
Jeżeli olej oprócz funkcji cieczy smarującej spełnia również funkcje cieczy roboczej w różnego rodzaju serwomechanizmach, układach automatycznych sterowania lub układach hydraulicznych, wówczas zmiana jego lepkości może spowodować poważne zaburzenia w pracy tych urządzeń. Z tego względu ciecz smarująca powinna, charakteryzować się możliwie najmniejszą zmiennością lepkości w zakresie temperatury występującej w czasie eksploatacji danego urządzenia. Tak więc dla eksploatującego ważna jest nie tylko odpowiednio dobrana lepkość oleju, ale również jej zmiany wraz ze zmianami temperatury. Im mniejsze zmiany lepkości wykazuje dany olej, tym wyższa jest jego wartość użytkowa.
Zakwalifikowanie oleju jako cieczy smarującej z określonym przeznaczeniem eksploatacyjnym wymaga zorientowania odbiorcy nie tylko w lepkości oleju, ale również w jej zmianach wraz ze zmianami temperatury.
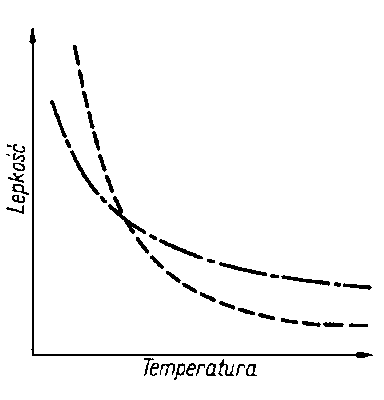Rys. 6.19. Dwie przykładowe krzywe zależności lepkości od temperatury

Rys. 6.20. Nomogram do wyznaczania lepkości oleju w zależności od temperatury

Zależność lepkości oleju od temperatury można przedstawić w postaci wzoru lub wykresu. Obydwie formy są do codziennych celów praktycznych zbyt skomplikowane i wymagają pewnego przygotowania teoretycznego. Zarówno w czasie produkcji, jak i do celów eksploatacyjnych, konieczne jest przedstawienie tej zależności w postaci możliwie najprostszej, zrozumiałej nawet dla niewykwalifikowanego personelu, a równocześnie jednoznacznej. Najlepszym sposobem byłoby przedstawienie tej zależności za pomocą jakiejś jednej liczby charakterystycznej.
Przy graficznym przedstawieniu wyników oznaczeń lepkości oleju w różnych temperaturach otrzymuje się krzywą wykładniczą (rys. 6.19).
Matematycznie zależność lepkości od temperatury przedstawia wzór Walthera (38)
(nt + c) T m = k (6.41)
gdzie: nt - lepkość kinematyczna w mm²/s, T - temperatura w K, c, k, m - stałe.

Po zlogarytmowaniu otrzymuje się
m lg T + lg lg (nt + c) = lg lg k (6.42)

W literaturze i normach (DIN) przyjmuje się c = 0,8, w normach amerykańskich c -= 0,65 - 0,75. W zależności od charakteru chemicznego i masy cząsteczkowej oleju odpowiednio dobrane wartości c zapewniają uzyskanie wyników obliczeń zgodnych z wynikami pomiarów.

Jeżeli przyjmie się lg lg k = A i m = B, c = 0,8, to
lg lg (nt + 0,8) = A - B lg T (6.43)

Po graficznym przedstawieniu zależności lepkości od temperatury otrzymuje się w układzie logarytmicznym, linię prostą nachyloną do osi temperatury pod pewnym kątem. Im kąt ten jest mniejszy, tym olej ma lepkość wykazującą mniejsze zmiany przy zmianach temperatury, a więc jest lepszy. W Stanach Zjednoczonych A.P. wykres taki nazywa się wykresem lepkości ASTM, a kąt nachylenia - kątem nachylenia prostej ASTM (ASTM - Slope).
Wzór Walthera służy do wyznaczenia prostej lepkości w układzie logarytmicznym, gdy jest znana lepkość oleju w co najmniej dwóch temperaturach. Z wyznaczonej prostej można znaleźć wartości lepkości dla temperatury, w której nie była ona mierzona. Opierając się na wzorze Walthera skonstruowano wykres w układzie współrzędnych IgTi lglg(ł'+0,8) służący do wyznaczania lepkości oleju w różnych temperaturach (rys. 6.20).
Nachylenie prostej lepkości m można obliczyć z następującej zależności
m = tg a = lg lg (n1 + 0,8) - lg lg (n2 + 0,8)
lg T1 - lg T2 		(6.44)

Oznaczając
w = lg lg (n + 0,8) (6.45)

otrzymamy
m = w1 - w2
lg T1 - lg T2 		(6.46)

Znając lepkość w dwóch temperaturach T1 i T2 można obliczyć lepkość w temperaturze T3 (K), wykorzystując zależność
w3 = m ( lg T1 - lg T3 ) + w1 = w1 - w2
lg T1 - lg T2		 ( lg T1 - lg T3 ) + w1 (6.47)

W tabl. 6.3 przedstawiono dokładność wyników uzyskiwanych z obliczeń. W podwyższonych temperaturach dokładność jest zadowalająca, natomiast w niskich temperaturach odchylenia są znaczne.

Tablica 6.3. Różnice między wartościami lepkości dwóch olejów obliczonych z wzoru Walthera a zmierzonymi

Temperatura °COlej 1Olej 2
lepkość kinematyczna, mm²/slepkość kinematyczna, mm²/s
zmierzonaobliczonaróżnicazmierzonaobliczonaróżnica
-17,729002300+60033005300-2000
25173,10165,00+8,10193,10192,00+1,10
3895,91--98,43--
5552,2953,0-0,7148,2949,00-0,71
9916,67--12,91--
12111,6111,10+0,518,448,10+0,34
1497,737,20+0,535,365,10+0,26
1775,475,10+0,373,763,52+0,24
2054,003,80+0,20---

6.2.5.3. Wysokość biegunowa

Jeżeli wykreśli się w układzie logarytmicznym proste lepkości dla wielu olejów otrzymanych z tej samej ropy, to po odpowiednim przedłużeniu w zakres niskiej temperatury proste te przetną się w jednym punkcie. Punkt ten zwany jest biegunem lepkości, rzędna tego punktu nazywa się wysokością biegunową (rys. 6.21). Wysokość biegunowa jest to lepkość jaką mają oleje tego samego pochodzenia w biegunie lepkości. Jeżeli podobne wykresy sporządza się dla olejów otrzymanych z innej ropy, to otrzyma się nową wiązkę prostych mających również swój biegun. Różne serie olejów będą więc miały różne bieguny lepkości leżące w przybliżeniu na jednej prostej zwanej prostą biegunową. Im większa jest wartość wysokości biegunowej, tym większa zmienność lepkości wraz ze zmianami temperatury olejów należących do danej serii. Wysokość biegunowa określa więc pochodzenie oleju niezależnie od jego lepkości.
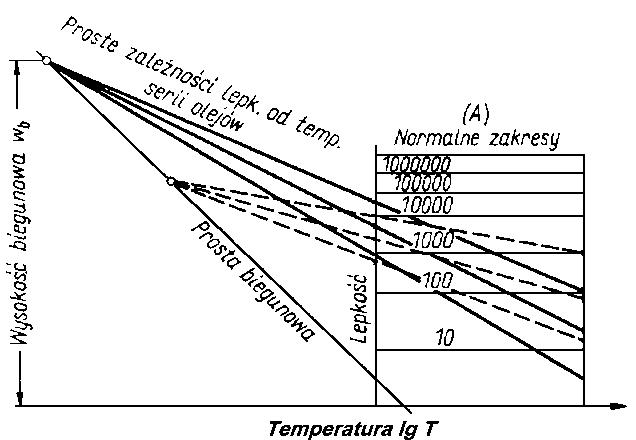Rys. 6.21. Zależności lepkości od temperatury; wysokość biegunowa; A -obszar zależności lepkości od temperatury zwykle przedstawiany na wykresach

Wysokość biegunową Wb można wyznaczyć z wykresu lub też obliczyć ze wzoru znając lepkość w dwóch dowolnych temperaturach
Wb = m ( lg T1 - 2,410 )+ w1
1 - 0,194 m 		(6.48)

6.2.5.4. Wskaźnik lepkości (indeks wiskozowy)

Wskaźnik lepkości jest wielkością charakteryzującą zmiany lepkości wraz ze zmianami temperatury. Jest to wielkość bezwymiarowa, gdyż zmiany lepkości badanego oleju są odnoszone do zmian lepkości olejów wzorcowych. Wielkość tę wprowadzili Dean i Davis w roku 1929 (35). Stopniowo została ona znormalizowana przez Komitety Normalizacyjne większości państw. Dean i Davis otrzymali dwie serie olejów wzorcowych z dwóch rop różniących się między sobą w zasadniczy sposób składem chemicznym.

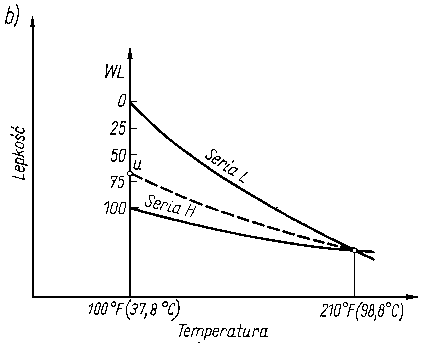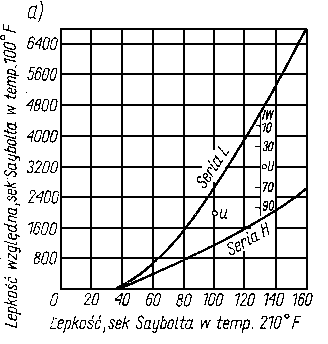
    Rys. 6.22. Graficzne przedstawienie sposobu wyznaczania wskaźnika lepkości WL:

    a) w układzie lepkości w 100°F i 210°F,

    b) w układzie temperatura-lepkość

Serię olejów o małej lepkości, ale i o małych zmianach lepkości wraz ze zmianami temperatury otrzymano z ropy pensylwańskiej o charakterze parafinowym. Oleje te nazwano olejami serii H (H = high = wysoki), o wysokiej odporności na zmiany temperatury, i przyjęto dla nich umownie wartość wskaźnika lepkości równą 100 jednostek.
Drugą serię olejów o dużej lepkości, ale i o dużych zmianach lepkości otrzymano z ropy kalifornijskiej o charakterze naftenowo-aromatycznym. Oleje te nazwano olejami serii L (L = Iow = niski), o niskiej odporności na zmiany temperatury, i przyjęto dla nich umownie wartość wskaźnika lepkości równą zero.
Dla olejów obu serii oznaczono lepkość (w sekundach Saybolta) w temperaturze 100 i 210°F, a otrzymane wyniki naniesiono na wykres o współrzędnych lepkości w 210°F i lepkości w 100°F (rys. 6.22a).
Opierając się na współrzędnych punktów ustalono równania parabol dla obu serii olejów, umożliwiające obliczanie lepkości w temperaturze 100°F dla oleju o dowolnej lepkości, jeżeli jest znana jego lepkość w temperaturze 210°F.
Dla olejów serii H lepkość y w temperaturze 100°F
y = 0,0408 x ² + 12,568 x - 475,4 (6.49)

a dla olejów serii L lepkość y w temperaturze 100°F

y = 0,02160 x² + 12,070 x - 721,2
gdzie: x - lepkość w temperaturze 210°F.

W ten sposób otrzymano krzywe dla wzorcowych serii olejów L i H. Umożliwia to porównywanie zmian lepkości badanego oleju U przy zmianach temperatury ze zmianami lepkości odpowiednich olejów serii wzorcowych.
Oznaczenie laboratoryjne lepkości badanego oleju U w temperaturze 100 i 210°F pozwala na znalezienie odpowiednich olejów wzorcowych. Odcinek rzędnej (rys. 6.22b) znajdujący się między dwoma krzywymi dzieli się na 100 części (dla oleju serii L wskaźnik lepkości WL = 0, a dla oleju serii H WL = 100).
Graficznie wskaźnik lepkości WL jest stosunkiem części rzędnej zawartej między krzywą L a punktem U, do części rzędnej zawartej między obu krzywymi L i H, czyli
WL = L - U
L - H		 • 100 (6.50)

Dean i Davis sporządzili tablicę określającą lepkości olejów wzorcowych od 40 do 160 sekund Saybolta w temperaturze 210°F.
W Polsce i wielu innych krajach wskaźnik lepkości wyznacza się opierając się na lepkości kinematycznej n50 i n100 wyrażonej w mm². Tablice dla olejów wzorcowych przeliczone zostały na odpowiednie lepkości w mm2/s. Dlatego wzór na wskaźnik lepkości został zmodyfikowany o poprawkę P wynikającą z przeliczenia lepkości na mm² i temperatury na °C. Zatem
WL = L - U
L - H		 • 100 + P (6.51)

gdzie: L - lepkość kinematyczna w mm²/s oleju wzorcowego serii L w temperaturze 50°C (olej ten ma w 100°C taką samą lepkość jak olej badany), H - lepkość kinematyczna w mm²/s oleju wzorcowego serii H w temperaturze 50°C (olej ten ma w 100°C taką samą lepkość jak olej badany), U - lepkość kinematyczna w mm²/s oleju badanego w temperaturze 50°C.

Graficzne przedstawienie wyznaczania WL w układzie temperatura - lepkość przedstawiono na rys. 6.22b.
Należy zaznaczyć, że mogą istnieć oleje, w których zmiany lepkości są mniejsze niż olejów serii H. Mają one wskaźniki lepkości wyższe niż 100. Oleje wykazujące większe zmiany lepkości niż oleje serii L mają wskaźniki lepkości ujemne. Praktycznie w celu wyznaczenia wskaźnika lepkości badanego oleju konieczne jest zmierzenie lepkości badanego oleju w temperaturze 50°C i 100°C. Pozostałe dane odnoszące się do olejów wzorcowych bierze się z tablic. Często przy szybkim obliczaniu wskaźnika lepkości posługujemy się wykresami i nomogramami. Znając lepkość oleju w temperaturze 50°C i 100°C w °E lub mm²/s, można bez trudu z takich nomogramów odczytać wskaźnik lepkości.
Stosowanie wskaźnika lepkości jest bardzo wygodne, ponieważ za pomocą jednej liczby uzyskuje się charakterystykę zmian lepkości oleju wraz ze zmianami temperatury. Im wyższa wartość wskaźnika lepkości WL, tym lepkość oleju jest mniej wrażliwa na zmiany temperatury. Wskaźnik lepkości jest więc ważnym kryterium oceny przydatności eksploatacyjnej olejów. Jest on zależny od wielu czynników, a przede wszystkim od składu chemicznego oleju, a więc pośrednio i od pochodzenia oraz sposobu przeróbki ropy naftowej.
Najmniejszymi zmianami lepkości wraz ze zmianami temperatury charakteryzują się związki parafinowe. Rozgałęzienie łańcucha zmniejsza wartość wskaźnika lepkości. Dla węglowodorów cyklicznych, tj. naftenowych i aromatycznych, wartość wskaźnika lepkości maleje wraz ze wzrostem ilości pierścieni w cząsteczce, a rośnie i to bardzo silnie, wraz z ilością bocznych łańcuchów parafinowych. Rozgałęzienie bocznych łańcuchów wpływa na obniżenie wartości wskaźnika lepkości.
Węglowodory składające się z samych pierścieni aromatycznych lub mieszanych mają bardzo małe wartości wskaźnika lepkości. Najmniejsze jednak jego wartości mają związki asfaltowo-źywiczne. Ogólnie rzecz biorąc, ze względu na własności lepkościowe, najbardziej pożądanym składnikiem olejów są węglowodory parafinowe oraz węglowodory aromatyczne i naftenowe z długimi bocznymi łańcuchami parafinowymi.
Natomiast niepożądanymi składnikami są węglowodory aromatyczne i aromatyczno-naftenowe o skondensowanych pierścieniach, a przede wszystkim związki asfaltowo-źywiczne.
Najmniejsze wartości wskaźnika lepkości mają oleje z rop asfaltowych, a więc o dużej zawartości węglowodorów aromatycznych i aromatyczno-naftenowych.
Największe wartości wskaźnika lepkości mają oleje z rop parafinowych (a więc o dużej zawartości węglowodorów parafinowych lub bocznych łańcuchów parafinowych) oraz oleje syntetyczne.
Z procesów technologicznych największy wpływ na wskaźnik lepkości ma rafinacja. Największymi wartościami wskaźnika lepkości odznaczają się oleje rafinowane selektywnymi rozpuszczalnikami.
Znaczenie wskaźnika lepkości z punktu widzenia teoretycznego, jak również praktycznego, ograniczone jest przez to, że zależność lepkości od tempera- tury podaje się w wąskich przedziałach (50- 100°C). Nie może więc on charakteryzować zachowania olejów w warunkach temperatury znacznie odbiegających od temperatury pomiaru lepkości.

6.2.6. Zależność lepkości olejów od ich budowy chemicznej

Lepkość, podobnie jak inne własności fizyczne cieczy, zależy od jej budowy chemicznej. Im większe cząsteczki składają się na ciecz, tym większe są oddziaływania międzycząsteczkowe, a więc większe siły kohezji i większa lepkość. Ciecz składająca się z dużych cząsteczek ma wysoką temperaturę wrzenia. Dlatego też między temperaturą wrzenia a lepkością występuje zależność powiązana za pośrednictwem masy cząsteczkowej. Zależność między masą cząsteczkową a lepkością wykorzystuje się do określania średniej masy cząsteczkowej cząsteczek polimerów przez pomiar lepkości. Na lepkość ma bezpośredni wpływ nie tylko wielkość cząsteczek, ale również to, z jakich atomów są one zbudowane i jak wygląda ich przestrzenne rozmieszczenie w cząsteczce. Zwiększenie rozgałęzienia cząsteczek prowadzi z reguły do zwiększenia lepkości, gdyż przy wzajemnym przemieszczaniu się, cząsteczki zaczepiają się rozgałęzieniami, które działają tu jak przestrzenne przeszkody.
Spośród trzech grup węglowodorowych, z których składają się oleje z ropy naftowej, najmniejszą lepkością odznaczają się węglowodory parafinowe. Ich lepkość zwiększa się z długością łańcucha i ze stopniem jego rozgałęzienia.
Z dwóch pozostałych grup węglowodorowych, nafteny o małych cząsteczkach mają większe lepkości niż węglowodory aromatyczne o małych cząsteczkach. Dla wielopierścieniowych naftenów i aromatów zachodzi odwrotny stosunek, gdyż wpływ kondensowanych pierścieni aromatycznych jest tu większy niż wpływ kondensowanych pierścieni naftenowych.
Rozpatrywanie wpływu budowy przedstawicieli poszczególnych grup węglowodorowych na lepkość ma ograniczony charakter, gdyż występujących w olejach węglowodorów nie można zaliczyć do jednej z grup węglowodorowych, bowiem na ich budowę składają się elementy należące równocześnie do dwóch lub nawet trzech grup. Tak np. może być węglowodór o dwóch pierścieniach aromatycznych, jednym naftenowym, mający jeszcze ponadto boczne łańcuchy parafinowe.
Dlatego rozpatrując wpływ budowy na lepkość należy rozpatrywać wpływ poszczególnych elementów budowy. Prace w tym kierunku zapoczątkowane zostały przez Hugela, Lerera, Landę i Suidę.
Do poznania wpływu tych elementów w bardzo znacznym stopniu przyczyniły się badania Mikeski [33], Schieslera [41] oraz Piłata i jego żony [39].
Autorzy ci syntezowali odpowiednie węglowodory i przez „doczepianie” do nich różnych elementów badali ich wpływ na lepkość. Stwierdzili, że w przypadku węglowodorów parafinowych lepkość najintensywniej wzrasta przy wprowadzeniu pierścienia naftenowego sześciowęglowego, w mniejszym stopniu przy pięcioczłonowym, a w najmniejszym stopniu przy wprowadzeniu pierścienia aromatycznego (rys. 6.23).
Lepkość wzrasta wraz ze zbliżaniem się wprowadzonego pierścienia ku środkowi łańcucha. Tak więc alkilopochodne monocyklicznych naftenów mają wyższe lepkości od alkilopochodnych aromatycznych. Lepkość pochodnych alkilowych wzrasta wraz z długością łańcucha alkilowego oraz ze wzrostem liczby pierścieni w cząsteczce.
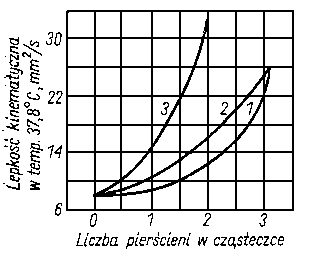    Rys. 6.23. Zależność lepkości od liczby pierścieni w cząsteczce wg Czarnożukowa;
  1. - pochodne etylofenylowe,
  2. - pochodne propylocyklopentylowe,
  3. - pochodne etylocykloheksylowe

Tablica 6.4. Wpływ rodzaju pierścienia węglowodorowego C20 na lepkość
(wg E. i St. Piłatów)

WęglowodórWzór strukturalnyLepkość kinematyczna mm²/s
w temperaturze 60°Cw temperaturze 98,9°C
1-fenyloeikozan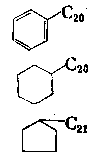6,663,33
l -cykloheksyloeikozan8,404,13
l -cyklopentyloheneikozan7,883,80

W tabl. 6.4 przedstawiono wpływ rodzaju pierścieni na lepkość, a w tabl. 6.5 - wpływ długości bocznych łańcuchów na lepkość.

Jak już wspomniano policykliczne węglowodory aromatyczne mają większą lepkość od policyklicznych naftenowych (tabl. 6.6). Tym też tłumaczy się wysoką lepkość związków asfaltowo-żywicznych.

Tablica 6.5. Wpływ długości bocznych łańcuchów węglowodorowych na lepkość
(wg E. i St. Piłatów)

WęglowodórLepkość kinematyczna mm²/s
w temperaturze 37,8°Cw temperaturze 98,9°C
C10H7—C6H135,051,50
C10H7—C18H3722,865,04
C10H7—C22H4535,486,41

Tablica 6.6. Wpływ rodzaju pierścieni na lepkość (wg E. Piłatowej)

WęglowodórLepkość kinematyczna mm²/s
w temperaturze 37,8°Cw temperaturze 98,9°C
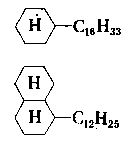7,20-
10,403,39
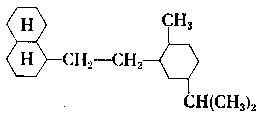31,465,40
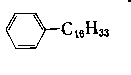5,66-
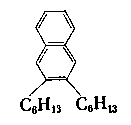12,23,33

Przy węglowodorach policyklicznych lepkość bardzo intensywnie podwyższają boczne łańcuchy parafinowe. Ich efektywność jest tym większa, im większa jest liczba łańcuchów (tabl. 6.7), im są one dłuższe (tabl. 6.5) i im bardziej rozgałęzione (tabl. 6.8 i 6.9).

Tablica 6.7. Wpływ liczby bocznych łańcuchów na lepkość (wg E. i St. Piłatów)

WęglowodórLepkość kinematyczna mm²/s
w temperaturze 38,8°Cw temperaturze 98,9°C
C6H5—C18H377,803,15
C6H4—(C18H37)248,809,82
C6H3—(C18H37)396,2014,90
C10H7—C6H135,202,00
C10H6—(C6H13)219,504,03
C10H5—(C6H13)334,005,60

6.2.7. Lepkość mieszanin

Lepkość nie jest wielkością addytywną. Zmieszanie ze sobą dwóch cieczy znacznie różniących się między sobą budową chemiczną powoduje znaczne odchylenia w stosunku do zależności prostoliniowej. Wszelkie przyczyny powodujące utrudnianie przemieszczania cząsteczek względem siebie, powodują zwiększenie lepkości.

Tablica 6.8. Lepkość rozgałęzionych węglowodorów parafinowych C26 w temperaturze 38°C (wg Cosly i Sutherlanda)

WęglowodórWzór strukturalnyLepkość w temperaturze 37,8°C mm²/sTemperatura krzepnięcia °C
5-n-butylodokozan
C4
│
C4—C—C17
11,4820,8
5,14-dwu-n-butylo-okta-dekan
C4—C—C8—C—C4
│
C4		│
C4
12,85,7
7-n-heksyloeikozan
C6—C—C13
│
C6
10,6910,2
3-etylo-5(2-etylo-butylo)okta-dekan
C2—C—C—C—C13
│
C2		│
C
│
C—C2
│
C2
--

Odwrotnie, jeżeli domieszanie drugiej cieczy ułatwia poślizg, lepkość mieszaniny jest mniejsza w porównaniu z cieczą wyjściową. W praktyce trybologicznej bardzo często konieczne jest mieszanie ze sobą dwóch olejów dla uzyskania mieszaniny o żądanych własnościach lepkościowych. Mieszanie ze sobą olejów jest dopuszczalne w tym przypadku, gdy nie zawierają one dodatków (np. bazy olejowe lub oleje typu regular), bowiem przy mieszaniu olejów z dodatkami zachodzi obawa oddziaływania

Tablica 6.9. Lepkości rozgałęzionych węglowodorów parafinowych C26 w temperaturze 100° C (zestawienie na podstawie tablic Obolencewa)

WęglowodórWzór strukturalnyLepkość w temperaturze 100°C mm²/sTemperatura krzepnięcia °C
n-heksakozanCH3—(CH2)21—CH33,2656,2
5-butylodokozan
CH3
│
(CH2)3
│
CH3—(CH2)3—CH—(CH2)16—CH3
2,9820,8
11-pentylo-heneikozan
    CH3—CH2—CH—CH2—CH3
│
CH3—(CH2)9—CH—(CH2)9—CH3
2,73-40

chemicznego dodatków ze sobą z wytworzeniem związków o niekorzystnym lub wręcz agresywnym działaniu. W celu uzyskania oleju o żądanej lepkości poprzez zmieszanie ze sobą olejów o dwóch różnych lepkościach, należy wiedzieć w jakim stosunku trzeba ją ze sobą zmieszać. Do obliczenia lepkości mieszaniny najlepiej nadaje się lepkościogram Molina-Gurwicza. Oparty jest on na wynikach pomiarów lepkości mieszanin dwóch olejów A i B, z których A miał lepkość E20 = 1,5°E, a B - E20 = 60°E. Skład mieszaniny był zmieniany w granicach od 0 do 100% obj. składnika A. Lepkościogram można stosować w następujący sposób. Chcąc znaleźć lepkość mieszaniny składającej się np. z 30% oleju o lepkości E20 = 12,5 i 70% oleju o lepkości E20 = 1,8 łączy się za pomocą prostej punkt 1,8 na skali B z punktem 72,5 na skali A (rys. 6.24). Z punktu odpowiadającego 30% składnika A
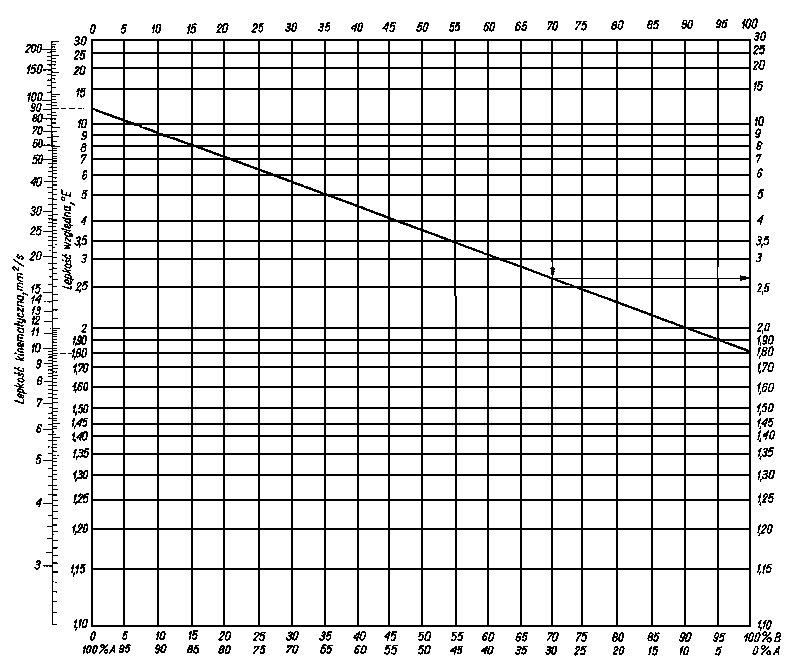Rys. 6.24. Nomogram do wyznaczania lepkości mieszanin olejów

(70% składnika B) opuszcza się prostą pionową do przecięcia z poprzednią wyznaczoną prostą. Następnie z punktu przecięcia obu prostych prowadzi się prostą równoległą do osi odciętych aż do przecięcia z osią rzędnych, na której odczytuje się poszukiwaną lepkość mieszaniny.

6.2.8. Lepkość emulsji i zawiesin

Emulsjami nazywa się układy dwóch nie mieszających się ze sobą cieczy, z których jedna jest rozproszona (rozdrobniona) w drugiej pod postacią kropelek. Warunek wzajemnej nierozpuszczalności cieczy ma podstawowe znaczenie, gdyż przy zmieszaniu dwóch cieczy rozpuszczalnych w sobie otrzymuje się roztwór.
Zawiesinami nazywa się układy dwóch nierozpuszczalnych w sobie ciał, z których jedno jest cieczą zawieszającą (dyspergującą) drobne cząstki ciała stałego (ciało zdyspergowane).
Zarówno w przypadku emulsji, jak i zawiesin, zachodzi podobna sytuacja, tj. w cieczy mamy rozdrobnione cząstki obcego ciała, którym mogą być kropelki drugiej cieczy lub cząstki ciała stałego. Pod działaniem sił ścinających następuje przemieszczanie się cieczy dyspergującej względem ciała zdyspergowanego. Tak więc oprócz tarcia wewnętrznego cieczy, mamy do czynienia z tarciem zewnętrznym na granicy rozdziału faz (rys. 6.25).
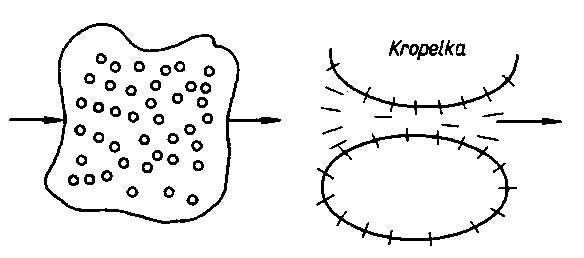Rys. 6.25. Model tarcia na granicy faz emulsji

Ze względu na to, że powierzchnie rzeczywistego kontaktu są bardzo duże, a więc i działające siły między cząsteczkowe, adhezyjne są duże, lepkość wzrasta bardzo znacznie. Przykładem mogą być różnego rodzaju majonezy (emulsja żółtka w oleju roślinnym), emulsje olejów mineralnych z wodą.
W przypadku zawiesin obecność cząstek ciała stałego w cieczy powoduje dodatkowo nadawanie cieczy charakteru cieczy nienewtonowskiej, z czym wiążą się różnego rodzaju anomalie lepkości.

6.2.9. Lepkość olejów zapowietrzonych

W układach olejenia wielu maszyn olej zemulgowuje stykające się z nim powietrze, tworząc z nim układ, w którym fazą zdyspergowaną jest powietrze, a fazą dyspergującą olej. Pozornie wydawać by się mogło, że wprowadzenie do oleju czynnika, którego lepkość jest znikoma, spowoduje zmniejszenie lepkości emulsji olejowo-powietrznej. Jednakże podobnie, jak w przypadku emulsji dwóch cieczy, tak i przy wprowadzeniu do oleju powietrza, lepkość emulsji olejowo-powietrznej ma nieco większą wartość niż oleju niezapowietrzonego.
Einstein [1] rozpatrywał problem lepkości ośrodka, w którym znajdują się kuliste cząstki ciała sztywnego całkowicie zwilżone cieczą dyspergującą. Doszedł do wniosku, że stosunek lepkości cieczy z zawiesiną hz do cieczy czystej ho wynosi
hz
ho		 = 1 + 0,025 b (6.52)
gdzie: b - procentowy (obj.) udział fazy rozproszonej.

Problem ten był rozpatrywany również przez Taylora [1], który założył, że rozproszone ciało jest cieczą o lepkości h`. Otrzymał on wzór na stosunek hz/ho
hz
ho		 = 1 + 0,025 b h` + 0,4 ho
h` + ho 		(6.53)

Jeżeli założy się, że zdyspergowane ciało jest nielepkie, to wyrażenie ułamkowe zbliża się do wartości 0,4, a całe równanie Taylora przybiera postać
hz
ho		 = 1 + 0,010 b (6.54)

Hayward [l] przeprowadził eksperymentalną weryfikację powyższych wzorów. Stosując specjalny lepkościomierz zmierzył lepkość olejów zapowietrzonych (do 25% powietrza) typu regular i olejów z dodatkami. Wartość „b” wyznaczył przez pozostawienie oleju w spokoju, co pozwalało na stopniowe wydzielenie się powietrza. Ustalił on empiryczną zależność
hz
ho		 = 1 + 0,015 b (6.55)

Stwierdził, że wpływ zapowietrzenia na lepkość olejów jest niewielki zarówno dla olejów z dodatkami, jak i olejów typu regular. Podany powyżej wzór ma zastosowanie do olejów o małych i dużych lepkościach. Jest on również słuszny w przypadku, gdy rozdrobnienie jest bardzo duże, jak i w przypadku, gdy banieczki powietrza są stosunkowo duże.

6.2.10. Dodatki zwiększające lepkość i wskaźnik lepkości oleju (wiskozatory)

6.2.10.1. Mechanizm działania

Istnieje wiele urządzeń, które ze względu na warunki w obszarach tarcia (wysoka temperatura, wysokie naciski jednostkowe itp.) muszą być smarowane olejami o dużej lepkości. Nie we wszystkich jednak ropach występują węglowodory o dużych lepkościach. Z wielu gatunków rop można otrzymać olej jedynie o małych i średnich lepkościach. W wielu ropach występują ciężkie frakcje olejowe, trudno je jednak uwolnić od towarzyszących im w bardzo dużej ilości związków asfaltowo-żywicznych, dlatego też proces otrzymywania ciężkich frakcji olejowych może być drogi, a czasami nieopłacalny.
W przypadku produkcji olejów smarowych z rop nie mających ciężkich frakcji olejowych konieczne jest nieraz zwiększenie lepkości olejów o małej i średniej lepkości przez wprowadzanie dodatków. Ma to szczególne znaczenie, gdy w danym kraju przerabia się tylko jeden typ ropy, a więc gdy braki w ciężkich frakcjach oleju nie mogą być uzupełniane olejami z przeróbki innych rodzajów ropy.
Bardzo często zwiększanie lepkości frakcji oleju uzyskuje się przez zmieszanie jej z brightstockiem - olejem pozostałościowym o charakterze parafinowo-naftenowym o bardzo dużej lepkości (n50 ≈ 300 mm²/s). Brightstock można otrzymać tylko z pewnych gatunków ropy przez odasfaltowanie propanowe, dlatego w wielu krajach brightstock pochodzi z importu.
Innym sposobem zwiększenia lepkości olejów jest wprowadzenie do nich związków o znacznej masie cząsteczkowej. Zazwyczaj są to ciekłe polimery. Dodatki podwyższające lepkość zwykle zwiększają również wskaźnik lepkości WL, a bardzo często polepszają zachowanie się oleju w niskiej temperaturze. Wydawać by się mogło, że stosowanie dodatków podwyższających lepkość jest doskonałym sposobem otrzymywania olejów o dużych lepkościach.
W wielu przypadkach stosowanie takich dodatków może być bardzo niebezpieczne. Tak np. w silniku istnieją warunki do częściowego odparowania składników oleju. Intensywność odparowania jest zazwyczaj większa u olejów o mniejszej lepkości, gdyż mają one niższą temperaturę wrzenia. Przy olejach zagęszczonych dodatkami, olej częściowo odparowuje pozostawiając zagęszczacz, co może spowodować zaklejenie lub zakoksowanie współpracujących elementów. Z tych względów ogranicza się zawartość zagęszczaczy do 1÷ 2% dla olejów lotniczych i 6 ÷ 8% dla olejów samochodowych.
Mechanizm podwyższenia lepkości przez dodatki zagęszczające oraz zmniejszenie zmian lepkości wraz ze zmianami temperatury nie jest jeszcze całkowicie wyjaśniony. Wielu autorów wraz ze Staudingerem - badaczem układów wielkocząsteczkowych uważa, że wprowadzenie do rozpuszczalnika o małej lepkości (w naszym przypadku oleju) cząsteczek polimeru o długiej nitkowatej budowie, silnie hamuje ruchy cząsteczek rozpuszczalnika, a więc zwiększa jego lepkość. Cząsteczka polimeru o takiej budowie ze względu na swą znaczną długość styka się z wieloma cząsteczkami rozpuszczalnika i oddzialywuje na nie siłami międzycząsteczkowymi. W ten sposób każda cząsteczka polimeru potrafi ,,unieruchomić" wiele cząsteczek rozpuszczalnika, a więc mała ilość dodatku potrafi silnie zwiększyć lepkość.
Niektórzy uważają, że długie nitkowate cząsteczki polimeru zginają się i tworzą kłębki. Wzrost temperatury powoduje rozwijanie się (pęcznienie) kłębka. Hamuje to obniżanie lepkości w podwyższonej temperaturze.
Wprowadzenie dodatków zagęszczających często powoduje zmianę charakteru cieczy z newtonowskiej na nienewtonowską.

6.2.10.2. Rodzaje dodatków

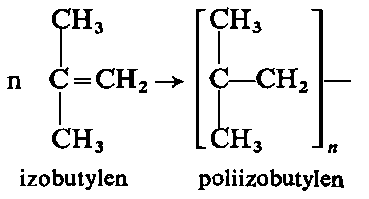
Dodatki zagęszczające zwane są często wiskozatorami. Zazwyczaj są to różnego rodzaju wielkocząsteczkowe polimery. Ostatnio największe zastosowanie znalazły jako ciekłe polimery dodawane do olejów poliakrylany, polimetakrylany oraz poliizobutyleny.
Rzadziej stosowane są różnego rodzaju kopolimery styrenu z olefinami, polimery kwasu fumarowego, polimery eteru winylowo-butylowego i woltole. Poliizobutyleny dla celów zagęszczania olejów dają najlepsze efekty, gdy mają masę cząsteczkową 10000-15000. Niemniej jednak, stosowane są również poliizobutyleny o mniejszych i większych masach cząsteczkowych.

Wiskozatory poliizobutylenowe mają różne handlowe nazwy Superol (ZSRR), Oppanol (firma BASF- RFN), Paraton i Exanol (firma Standard Oil - USA).
Polimetakrylany i poliakrylany wprowadzane do olejów mają zazwyczaj masy cząsteczkowe 10 000 - 20 000.
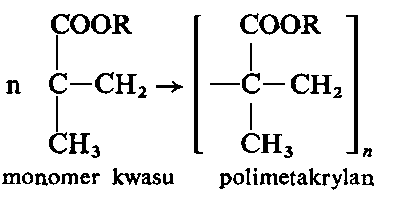
gdzie: R-grupy alkilowe wprowadzane podczas estryfikacji kwasu metakrylowego różnymi alkoholami.

Dodatki polimetakrylanowe i akrylanowe również mają różne nazwy handlowe: Montovis (firma Monsanto), Viscoplex i Plexol (RFN), Acryloids (USA), Vindex (Węgry), Glisoviscal, Garbacryl, Empicryl i inne.
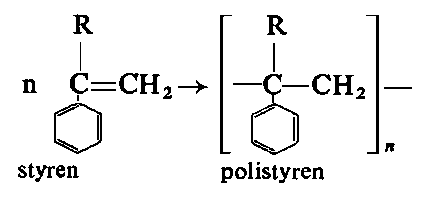
Rzadziej są stosowane dodatki polistyrenowe o masie cząsteczkowej 10000-20000.

Mają one handlowe nazwy, np. Santodex (firma Monsanto). Ostatnio stosowane są również w niektórych krajach polimery kwasu fumarowego (kwasu trans-eteno-dwukarboksylowego COOHCH═CHCOOH).
Polimery eteru winylo-n-butylowego są stosowane głównie w Związku Radzieckim pod nazwą Winipolu.
Woltole są to produkty otrzymywane z olejów roślinnych lub mieszanin olejów roślinnych z mineralnymi, pod działaniem cichych wyładowań elektrycznych (200-3000 okresów/s przy napięciu 2000-20000 V), w atmosferze gazu obojętnego. Olej poddawany wyładowaniom w cienkich warstwach ogromnie zwiększa swoją lepkość, gdyż wyładowania powodują kondensację i polimeryzację cząsteczek.
Bardzo poważną wadą zagęszczaczy jest ich mała odporność na oddziaływanie mechaniczne i działanie wysokiej temperatury. W wyniku oddziaływań mechanicznych, polimery ulegają degradacji (zmniejszenie masy cząsteczkowej), co powoduje zmniejszenie lepkości w czasie eksploatacji, a więc zaburzenia w procesie smarowania. Przy smarowaniu elementów pracujących w stosunkowo wysokiej temperaturze polimery mogą ulegać rozkładowi termicznemu połączonemu z zakoksowaniem powierzchni.

6.2.10.3. Mechaniczna degradacja dodatków polimerowych (ścinanie polimerów)

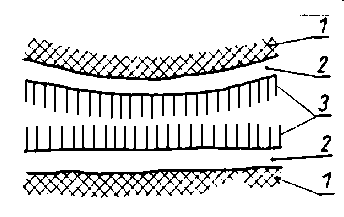
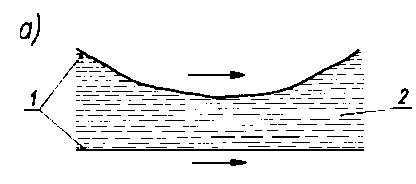
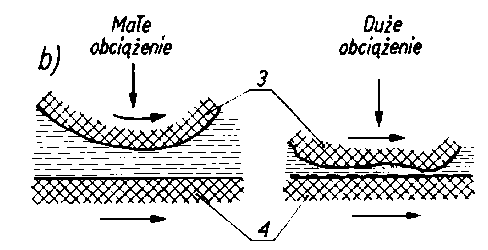
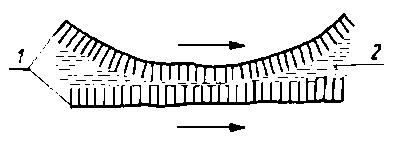
Oleje, których lepkość została zwiększona przez wprowadzenie polimerów, zmniejszają swoją lepkość podczas pracy w urządzeniach. Stwierdzono, że przyczyną zmniejszenia lepkości jest zmniejszenie masy cząsteczkowej wprowadzonych polimerów. Zjawisko to jest określane nazwą ścinania lub mechanicznej degradacji polimerów (rys. 6.26a). Występuje ono przy dużych prędkościach ścinania podczas tarcia przy
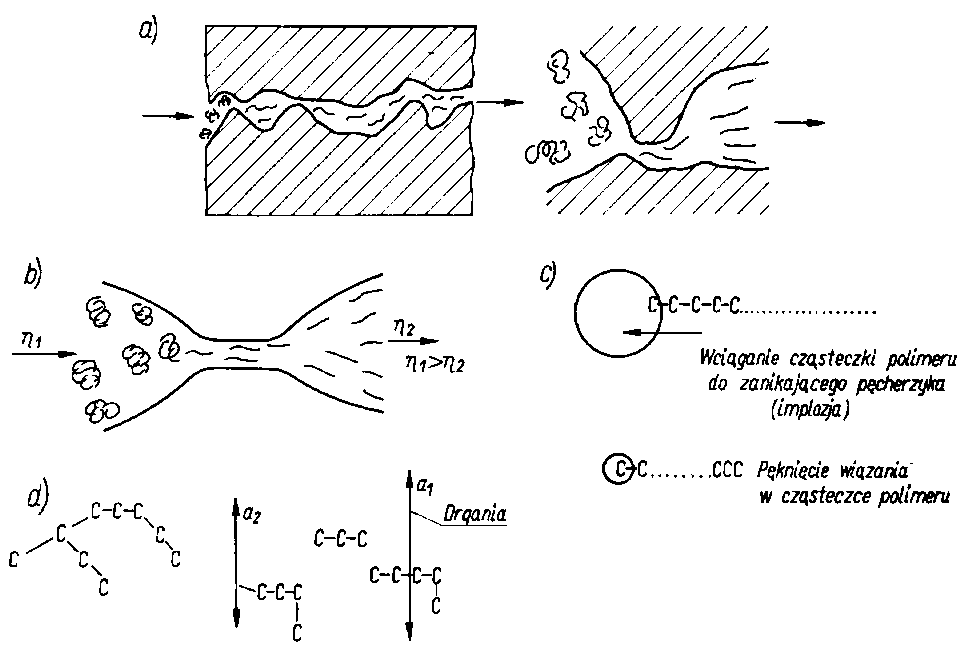    Rys. 6.26. Degradacja-ścinanie polimerów (wg Wiślickiego):
  1. degradacja-przez tarcie, ścinanie mechaniczne,
  2. degradacja przez dławienie,
  3. degradacja kawitacyjna,
  4. degradacja w polu akustycznym;
    a = amplituda drgań

wysokich naciskach jednostkowych, podczas przeciskania cieczy przez szczeliny, podczas kawitacji, przy działaniu fal ultradźwiękowych itd. Pomimo, że wymienione oddziaływania mechaniczne powodują zmniejszanie masy cząsteczkowej istnieją również poglądy, że bezpośrednią przyczyną rozrywania łańcuchów polimerów jest energia cieplna, powstała w mikroobszarach styku na skutek oddziaływania mechanicznego (miażdżenia, ucierania lub ugniatania cieczy roboczej). Niezależnie od tego czy degradacja zachodzi bezpośrednio pod działaniem sił ścinających, czy też poprzez oddziaływanie cieplne, ważny jest negatywny efekt obniżenia lepkości.

Degradacja polimerów poprzez działanie fal ultradźwiękowych ma zasadnicze znaczenie w badaniach odporności na ścinanie olejów zagęszczonych, gdyż stanowi najszybszy sposób obniżenia masy cząsteczkowej zagęszczaczy. Działanie fal ultradźwiękowych o odpowiednio wielkich amplitudach powoduje rozrywanie cząsteczek. Wielkie nitkowate, poplątane cząsteczki polimerów o dużej bezwładności nie nadążają za ruchami drgającymi rozpuszczalnika, a powstające w ten sposób siły tarcia są wystarczające do zerwania wiązań między atomami w cząsteczce.
Dodatkowo podczas działania fal ultradźwiękowych mamy zazwyczaj do czynienia z kawitacją. Przy rozchodzeniu się fal ultradźwiękowych powstają kolejno po sobie zagęszczenia i rozrzedzenia cieczy, prowadzące do tworzenia się i zanikania pęcherzyków kawitacyjnych. Czas życia pęcherzyka kawitacyjnego jest rzędu kilkudziesięciu mikrosekund. Przy jego tworzeniu i zanikaniu (implozja) cząsteczki najmniej ruchliwe, a więc cząsteczki polimeru, podlegają działaniu gwałtownych sił rozrywających. W otoczeniu pęcherzyka wzrasta również temperatura powodując dodatkowy efekt destrukcyjny. W maszynach i urządzeniach mamy w wielu przypadkach do czynienia ze zjawiskami kawitacyjnymi w układach olejenia (odrywania się cieczy smarnej od powierzchni, zawirowywania w czasie przepływu, gwałtowne gradienty ciśnienia w strukturze itp.) prowadzącymi do mechanicznej degradacji polimerów.

6.2.10.4. Metody badania odporności olejów na ścinanie

Wprowadzanie polimerów (wiskozatorów) do olejów ma na celu zwiększenie lepkości do wartości wymaganej w danym urządzeniu. Jeżeli w wyniku ścinania polimeru lepkość oleju obniża się, to wówczas olej zostaje zdyskwalifikowany jako ciecz smarująca do danego urządzenia. Jednym z podstawowych kryteriów oceny przydatności eksploatacyjnej olejów z polimerami jest określenie ich odporności na ścinanie. Badanie tego rodzaju możemy prowadzić w warunkach eksploatacyjnych lub w warunkach laboratoryjnych.
Badania laboratoryjne mogą mieć na celu albo odwzorowanie warunków eksploatacyjnych (badania takie trwają zazwyczaj bardzo długo), albo zrealizowanie ścinania w możliwie krótkim czasie dla uzyskania szybkich informacji o przydatności oleju.
W celu określania odporności olejów na ścinanie stosuje się najczęściej następujące urządzenia:
1) Urządzenia typu pompa-szczelina. W urządzeniach tych olej zazwyczaj jest tłoczony w obiegu zamkniętym przez pompę zębatą, tłoczkową lub łopatkową. Rolę szczeliny spełnia zawór ciśnieniowy, wtryskiwacz silnika wysokoprężnego lub element o większej liczbie otworów.
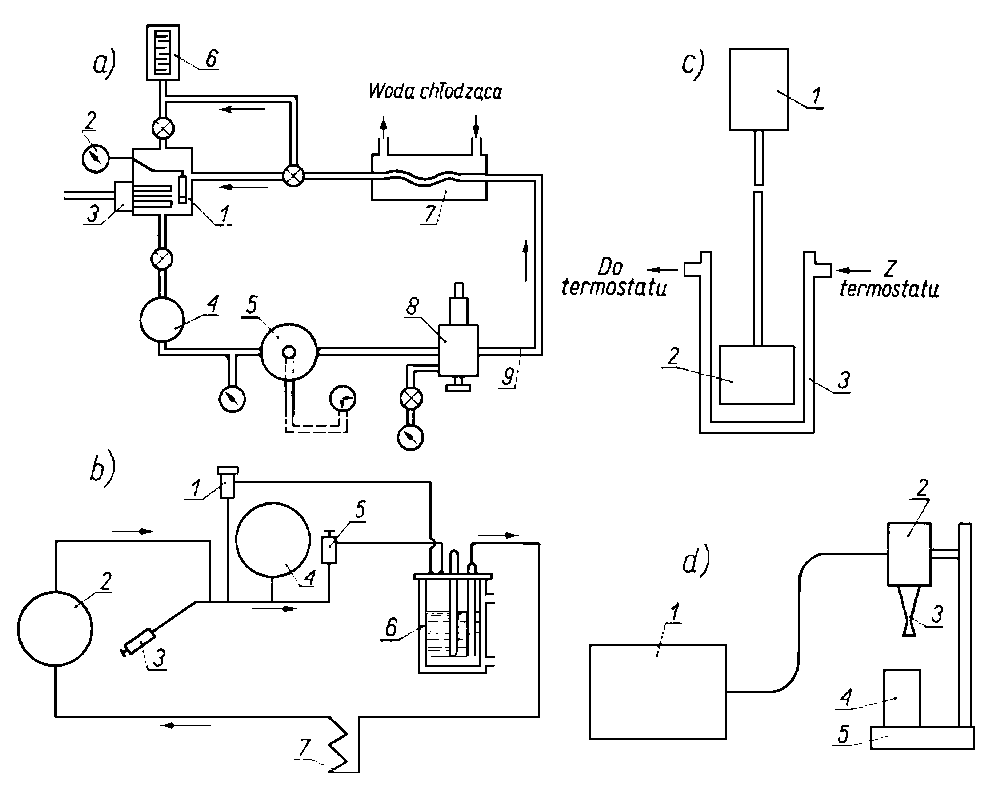Rys. 6.27. Schematy urządzeń do mechanicznego ścinania olejów:
a) urządzenie typu pompa-szczelina:
  1. - zbiornik główny,
  2. - termometr,
  3. - grzejnik nurkowy,
  4. - filtr,
  5. - pompa,
  6. - naczynie pomiarowe,
  7. - naczynie chłodzone,
  8. - zawór,
  9. - dławienie labiryntowe;
    b) urządzenie typu pompa-szczelina:
  1. - zawór bezpieczeństwa,
  2. - pompa,
  3. - zawór spustowy,
  4. - manometr,
  5. - zawór dławiący,
  6. - zbiornik oleju,
  7. - chłodnica;
    c) mieszadło ścinające:
  1. - silnik elektryczny napędzający,
  2. - mieszadło,
  3. - naczynie pomiarowe;
    d) promiennik ultradźwięków:
  1. - generator,
  2. - przetwornik
  3. - sonotroda,
  4. - naczyńko na ciecz,
  5. - statyw

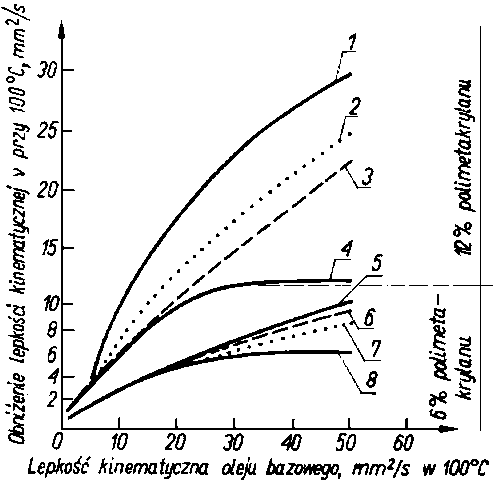    Rys. 6.28. Odporność polimerów na ścinanie przy badaniu różnymi metodami olejów różniących się lepkościami (wg Rossa);
    1. - badania eksploatacyjne (przekładnia),
    2. - maszyna FZG (po 7 godzinach),
    3. - wtryskiwacz,
    4. - aparat ultradźwiękowy,
    5. - badania eksploatacyjne,
    6. - maszyna FZG (po 7 godzinach),
    7. - wtryskiwacz,
    8. - aparat ultradźwiękowy

Przykładowe urządzenia tego rodzaju przedstawione są na rys. 6.27, Znaczny efekt ścinania uzyskuje się już po kilku cyklach przejścia oleju przez szczelinę (wtryskiwacz) (rys. 6.28).

2) Urządzenia do badania kół zębatych (np. maszyna FZG), w których zagęszczacz polimerowy jest degradowany podczas współpracy zębów dwóch kół zębatych.
3) Urządzenia ultradźwiękowe (generatory ultradźwiękowe). Intensywność ścinania zależy od mocy generatora ultradźwięków, częstotliwości drgań, profilu elementu wysyłającego drgania (koncentratora) itp. Badania za pomocą urządzeń ultradźwiękowych mają tę zaletę, że wymagają małej ilości cieczy do badań (kilka do kilkudziesięciu cm³) i dają już po krótkim czasie znaczny efekt ścinania (zazwyczaj kilkanaście minut).
4) Szybkoobrotowe mieszadła, homogenizatory, lepkościomierze rotacyjne itp. W urządzeniach tych znaczniejsze efekty ścinania uzyskuje się dopiero przy dużej prędkości obrotowej (ok. 20 000 obr/min).
Do badań laboratoryjnych można zaliczyć również badania odporności oleju na ścinanie prowadzone z wykorzystaniem silnika spalinowego zamontowanego na stanowisku hamownianym. Badania te są długotrwałe i drogie (obsługa silnika, koszt paliwa itp.)
Badania eksploatacyjne są prowadzone podczas normalnej eksploatacji samochodów. Wyniki badań eksploatacyjnych i hamownianych są obarczone błędem wynikającym z obniżenia lepkości wskutek rozcieńczenia oleju niespalonym paliwem. Aby ten błąd wyeliminować niejednokrotnie badania prowadzi się wykorzystując samochody napędzane płynnym gazem. 3 obiegi przez aparaturę wtryskową,
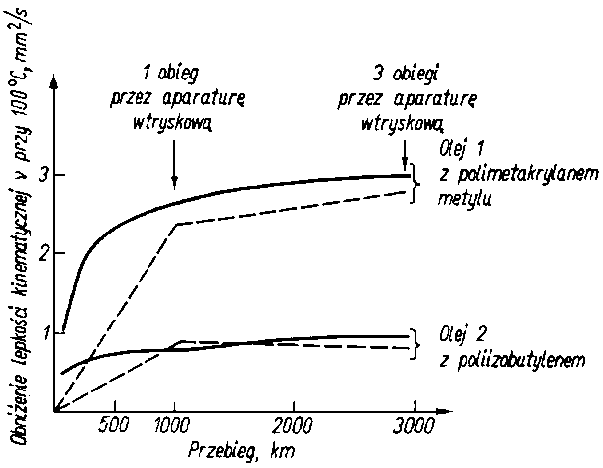Rys. 6.29. Wyniki badań odporności na ścinanie olejów zagęszczonych polimerami; linia ciągła - badania eksploatacyjne, linia przerywana - badania na aparacie wtryskowym

Porównanie efektów ścinania uzyskiwanych za pomocą różnych urządzeń przedstawiono na rys. 6.28 i 6.29. W przypadku olejów o zawartości 6% polimeru otrzymuje się bardzo zbliżone efekty ścinania przy badaniach eksploatacyjnych samochodowych i badaniach za pomocą aparatury wtryskowej silnika wysokoprężnego. Badania przeprowadzone w przypadku olejów o większej zawartości polimeru (12%) dają większą rozbieżność pomiędzy poszczególnymi metodami badań.
Ocenę odporności oleju na ścinania (ONS) prowadzi się opierając się na obniżeniu lepkości obliczanej ze wzoru
ONS = lepkość oleju świeżego - lepkość oleju po ścinaniu
lepkość oleju świeżego 		• 100

(W literaturze anglosaskiej ONS oznacza się skrótem SSI - Shear Stability Index).

Wyraża się również odporność na ścinanie odniesioną do polimeru ONSpol
ONSpol = lepkość oleju świeżego - lepkość oleju po ścinaniu
lepkość oleju świeżego - lepkość oleju bez polimeru		 • 100

W literaturze anglosaskiej jest również stosowane pojęcie lepkościowej efektywności polimeru
Lepkościowa efektywność polimeru = 100 - ONSpol

Autorzy książki wprowadzili inny sposób oceny intensywności ścinania polegający na wydzielaniu zdegradowanego polimeru z oleju i określaniu jego masy cząsteczkowej. W ten sposób można uzyskać znacznie więcej informacji o wpływie warunków eksploatacyjnych na odporność polimeru na ścinanie niż z obniżenia lepkości.

6.2.10.5. Wpływ budowy chemicznej dodatku polimerowego na jego odporność na ścinanie

Intensywność degradacji dodatku polimerowego zależy od tego, co podlega ścinaniu i w jakich warunkach. Na warunki ścinania składają się: temperatura, czas, wartość naprężenia i prędkość ścinania. Wpływ tych czynników poglądowo przedstawiono na rys. 6.30 i 6.31. Spośród czynników chemicznych największą rolę spełniają: rodzaj poddawanego ścinaniu dodatku, jego stężenie w oleju i średnia masa cząsteczkowa, rozrzut wartości masy cząsteczkowej, budowa przestrzenna polimeru (długość cząsteczki, boczne łańcuchy itp.).
Dla polimerów stosowanych jako wiskozatory można ustalić następujące prawidłowości:
Wzrost efektywności
w podwyższaniu wskaźnika
lepkości i lepkości 		↑ Poliakrylany
Polimetakrylany
Polifumarany
Poliizobutyleny
↓ Wzrost
odporności
na ścinanie

Im większa cząsteczka, a więc im większa masa cząsteczkowa, tym polimer łatwiej ulega ścinaniu. Dla każdego naprężenia ścinającego można ustalić „krytyczną" masę cząsteczkową, powyżej której odporność na ścinanie gwałtownie maleje. Zależność tą przedstawiono na rys. 6.30 d.
Jeżeli rozrzut wartości masy cząsteczkowej polimeru jest duży, wówczas efekt ścinania jest mniejszy niż w przypadku polimerów o jednorodnym składzie cząsteczkowym.
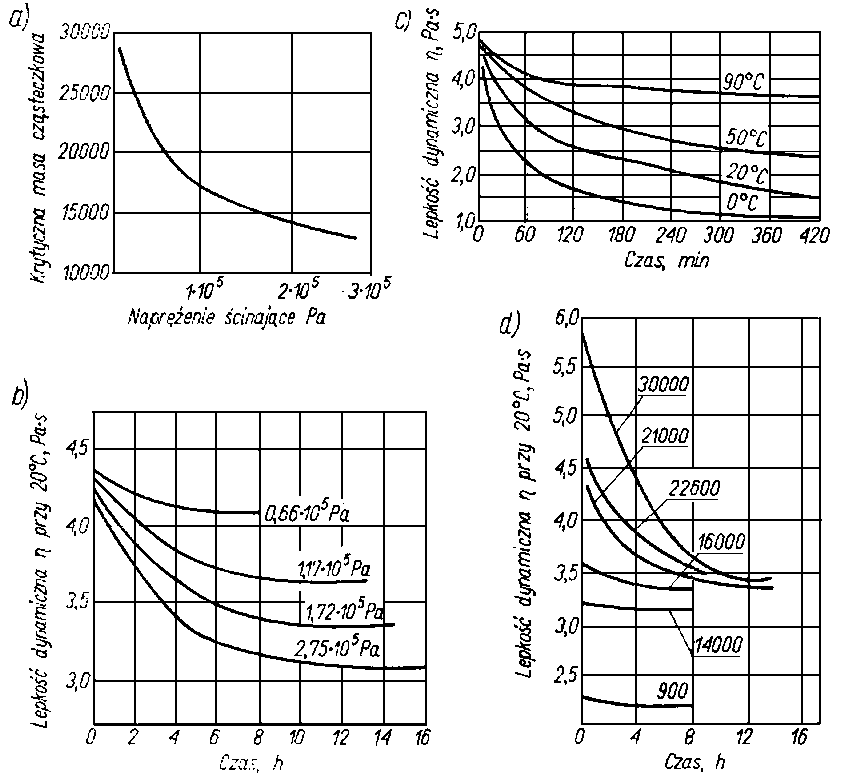    Rys. 6.30. Wpływ ścinania na zmiany lepkości oleju zagęszczonego polimerami (wg Siemienido):
  1. zależność krytycznej masy cząsteczkowej od wartości naprężenia ścinającego,
  2. zmiany lepkości roztworu w oleju, poliizobutylenu o masie cząsteczkowej 21000 przy różnych wartościach naprężenia ścinającego,
  3. zmiana lepkości 5-proc. roztworu poliizobutylenu. Mc = 30000 w oleju turbinowym przy ścinaniu w temperaturach 0, 20 i 90°C,
  4. zmiany lepkości 5% roztworu poliizobutylenu o różnej masie cząsteczkowej przy działaniu naprężenia ścinającego równego 0,172 Pa

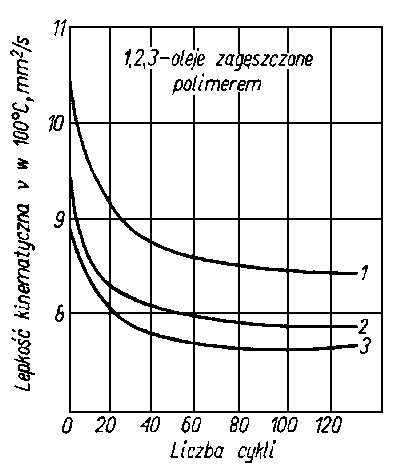    Rys. 6.31. Zależność lepkości od liczby cykli przy ścinaniu polimerów; 1,2,3-oleje zagęszczone polimerami

6.2.11. Eksploatacyjne znaczenie lepkości

Lepkość jest jedną z własności mających największe znaczenie w eksploatacyjnej przydatności oleju. Duża lepkość oleju wprowadzonego w skojarzenie tarciowe utrudnia wyciśnięcie go spomiędzy trących elementów, a więc zabezpiecza te elementy przed ich zatarciem. Duża lepkość, czyli duże opory tarcia wewnętrznego, powodują jednak znaczne straty mocy pracującego urządzenia. Tak więc dobór lepkości oleju musi uwzględniać dwa przeciwstawne dążenia, tj. dążenie do uzyskania trwałej warstwy oleju i dążenie do możliwie małych oporów tarcia skojarzenia. Przy doborze lepkości oleju do jakiegoś urządzenia, bierze się pod uwagę przede wszystkim warunki w jakich będzie on pracował, a więc temperaturę, obciążenie i jego zmiany w czasie oraz prędkość obrotową lub liniową.
Im wyższa temperatura i im wyższe obciążenie smarowanych skojarzeń, tym olej musi mieć większą lepkość. Natomiast im większa prędkość liniowa, tym mniejszą lepkość dobiera się ze względu na to, że przy dużej prędkości o wiele łatwiejsze jest utworzenie klina smarującego, a duża lepkość powoduje niepotrzebne straty mocy.
Do prawidłowej pracy urządzenia nie wystarcza tylko dobranie odpowiedniej lepkości, ale lepkość musi jak najmniej zmieniać się wraz ze zmianami temperatury, gdyż zazwyczaj temperatura wzrasta w czasie pracy urządzenia, co powoduje zmniejszenie lepkości.
Na skutek zmniejszania lepkości oleju wraz z podwyższeniem temperatury obniża się zazwyczaj ciśnienie w układzie olejenia. Może to powodować niedostateczny dopływ oleju do obszarów tarcia. Szczególnie niebezpieczne jest to w wysokich temperaturach.
W silnikach o złym stanie technicznym, wskutek zwiększenia luzów między współpracującymi częściami, trudniejsze jest uszczelnienie pierścieni tłokowych, uzyskanie odpowiednio grubej warstwy oleju w łożyskach itp. przy stosowaniu oleju o małej lepkości.
Przy obniżaniu temperatury, zwłaszcza w zimie, gdy lepkość oleju wzrasta, powstają trudności w uruchomieniu urządzenia, np. silnika.
Nadmierny wzrost lepkości oleju może poważnie utrudniać pracę pompy oleju, co wyraźnie wpływa na jej wydajność. Z tych wszystkich względów dobór oleju o odpowiednich własnościach lepkościowych ma bardzo poważne znaczenie.
W czasie pracy oleju w urządzeniach, lepkość oleju zmienia się. W wyniku procesów polimeryzacyjnych i kondensacyjnych oraz procesów utleniania, lepkość zwiększa się. W czasie pracy oleju w tłokowych' silnikach spalinowych, niespalone paliwo powoduje rozcieńczenie oleju i zmniejszenie jego lepkości. Zjawisko to jest szczególnie nasilone w okresie eksploatacji zimowej, natomiast w znacznie mniejszym stopniu obserwuje się go podczas eksploatacji w ciepłych porach roku. Zazwyczaj zmniejszenie lepkości w wyniku rozcieńczenia paliwem jest większe niż wzrost lepkości w wyniku procesów starzenia, co prowadzi ostatecznie do stopniowego zmniejszania się lepkości oleju w czasie pracy w silnikach. W urządzeniach, w których olej nie ulega rozcieńczeniu, procesy starzenia powodują stopniowy wzrost lepkości oleju.
    

6.3. Smarowanie hydrodynamiczne

Smarowanie hydrodynamiczne to rodzaj smarowania polegający na powstawaniu pomiędzy odpowiednio ukształtowanymi powierzchniami, na skutek ich względnego ruchu, warstwy cieczy, w której wytwarza się ciśnienie równoważące zewnętrzne obciążenie przy całkowitym oddzieleniu od siebie współpracujących powierzchni.
Zasadę powstawania wzrostu ciśnienia cieczy między przemieszczającymi się, nachylonymi względem siebie powierzchniami przedstawia model pokazany na rys. 6.32. Składa się on z płytki wykonanej z polimetakrylanu metylu, w której
    Rys. 6.32. Poglądowe przedstawienie wzrostu ciśnienia dynamicznego cieczy w szczelinie

    Rys. 6.33. Schemat czopa i panwi w badaniach Towera

zamocowano kilka szklanych rurek. Położenie płytki względem powierzchni oporowej, pokrytej warstwą oleju, ustala się śrubami regulacyjnymi. Ruch płytki względem powierzchni oporowej powoduje powstawanie ciśnienia dynamicznego w cieczy. Miarą tego ciśnienia w punktach położonych pod każdą z rurek jest wysokość podniesienia się cieczy. Obwiednia wysokości słupa cieczy w poszczególnych rurkach tworzy przybliżony rozkład ciśnienia hydrodynamicznego powstającego w wyniku ruchu płytki.

Zjawisko powstawania ciśnienia dynamicznego w wyniku względnego ruchu warstw cieczy odkrył przypadkowo, w końcu XIX wieku, Tower. Wykonywał on pracę badawczą mającą na celu opracowanie optymalnej metody smarowania wagonowych łożysk nośnych. Badał przedstawione na rys. 6.33 łożysko z niepełną panwią, stosując smarowanie za pomocą smarownicy knotowej, poduszki olejowej i kąpieli olejowej. Wyniki badań przy kąpieli olejowej wykazały nadspodziewanie małe, w porównaniu z pozostałymi rodzajami smarowania, współczynniki tarcia.
W czasie badań wywiercono w mosiężnej panwi otwór do zainstalowania smarownicy. Otwór ten zamknięto na okres pracy łożyska drewnianym czopem. Po uruchomieniu urządzenia stwierdzono, że olej wypiera czop z otworu. Zamontowany w otwór manometr wskazał, że rzeczywiste ciśnienie oleju jest dwukrotnie wyższe od ciśnienia średniego obliczonego na jednostkę pola rzutu powierzchni łożyska.
Podczas dalszych doświadczeń przeprowadzono pomiary ciśnienia w różnych punktach łożyska uzyskując jego rozkład.
Reynolds na podstawie doświadczenia Towera doszedł do wniosku, że działanie oleju było zjawiskiem hydrodynamicznym, związanym z lepkością oleju.
Technicznym przykładem wykorzystania omówionego zjawiska jest typowe współczesne ślizgowe łożysko poprzeczne z rys. 6.34. Czop łożyska obciążony siłą o kierunku BE zaczyna się obracać przy bezpośrednim zetknięciu z panewką w obszarze po przeciwnej stronie przyłożonego obciążenia (punkt E). Z chwilą, gdy
    Rys. 6.34. Zasada powstawania hydrodynamicznego klina oleju;
    1 - czop,
    2 - panewka,
    3 - klin olejowy

    Rys. 6.35. Rozkład ciśnienia p w hydrodynamicznej warstwie cieczy łożyska ślizgowego

czop zacznie się obracać, przesuwa się on w lewo i w górę w kierunku punktu A. Stopniowo wzrasta prędkość obrotowa wału. Wskutek tego tworzy się klin (DEA) cieczy wypierający wał w położenie przedstawione na rysunku. Klin powstaje na skutek tego, że w wyniku tarcia wewnętrznego w cieczy czop „porywa” za sobą olej. Warstwy oleju zaczynają się poruszać z prędkością wynikającą z gradientu, jaki wytwarza się między czopem a panewką. Siły tarcia wewnętrznego (lepkość) sprawiają, że w ruchu tym bierze udział cała ciecz, z wyjątkiem nieruchomych warstw przyściennych czopa i panewki. Dla cieczy smarującej musi być spełnione równanie ciągłości przepływu
QD = QE = QA = const (6.56)

gdzie: Q - natężenie przepływu cieczy.

Ponieważ pola przekroju strugi w punktach D, E, A są różne, więc w miarę zmniejszania przekroju poprzecznego musi się tworzyć strefa nadciśnienia, zaś w miarę jego zwiększenia strefa podciśnienia.
W rezultacie takiego rozkładu ciśnień, przedstawionego na rys. 6.35, na powierzchnię obracającego się czopa działają prostopadle do jego powierzchni dodatkowe siły. W strefie nadciśnienia są one skierowane w kierunku osi czopa i równoważą zewnętrzne obciążenie łożyska, zaś w strefie podciśnienia - przeciwnie.
Powstające w warstewce cieczy siły normalne działają w kierunku przesunięcia osi obrotu czopa, który wskutek tego opuszcza najniższe położenie, jakie zajmowałby, gdyby znajdował się tylko pod wpływem obciążeń zewnętrznych i własnego ciężaru. Przy obrocie czopa w kierunku strzałki (rys. 6.35) czop przemieszcza się w prawo, tj. w kierunku swego obrotu.
Gdyby na czop działały tylko siły tarcia wewnętrznego w cieczy, to powinien się on przesunąć przeciwnie do kierunku swego obrotu, tocząc się po wewnętrznej powierzchni panewki. Przemieszczenie takie obserwuje się w przypadku tarcia suchego (np. sworzeń i rolka koła napędowego ciągnika gąsienicowego).
W rzeczywistości, w przypadku istnienia między czopem a panewką warstwy cieczy, obserwuje się współdziałanie obydwu wymienionych efektów. Ponieważ wpływ sił wynikających z bezpośredniego działania tarcia wewnętrznego w cieczy jest mniejszy niż wpływ ciśnienia, które jest wtórnym rezultatem działania tarcia wewnętrznego, dlatego też czop przemieszcza się w kierunku swego obrotu.
Szczegółową analizę zjawisk w cieczy podczas smarowania płynnego przedstawia hydrodynamiczna teoria smarowania. Oparta jest ona na skomplikowanej matematycznej analizie ruchu cieczy i zawiera wiele zawiłych i rachunkowo żmudnych wyprowadzeń.
Ruch cieczy i towarzyszące mu zjawiska są często analizowane w hydrodynamicznej teorii smarowania, w układzie przedstawionym na rys. 6.36, równo
    Rys. 6.36. Modelowanie rzeczywistego klina olejowego:
    a) klin rzeczywisty,
    b) klin modelowy

ważnym omawianemu dotychczas łożysku poprzecznemu. Na rysunku tym pokazano rzeczywisty klin olejowy utworzony podczas współpracy czopa z panewką oraz równoważny klin zredukowany do powierzchni płaskiej, stosowany w rozważaniach matematycznych. Czop wału zastąpiono tu płaską powierzchnią przemieszczającą się z prędkością liniową równą prędkości obwodowej czopa.

    

6.4. Podstawowe równania tarcia płynnego

W hydrodynamicznej teorii smarowania rozważa się równania wynikające z praw zachowania masy (równanie ciągłości), pędu (równanie ruchu - Naviera-Stokesa) i energii (równanie energii). Z reguły zasadę zachowania masy i pędu ujmuje się jednym równaniem, zwanym równaniem Reynoldsa. Ponadto, w miarę potrzeby, w analizie uwzględnia się równania opisujące własności oleju (lepkość, gęstość, przewodność cieplna) i odkształcenie powierzchni ograniczających warstwę oleju (równanie sprężystości).

6.4.1. Równanie Naviera-Stokesa

W cieczy lepkiej w trzech wzajemnie prostopadłych płaszczyznach można wyróżnić trzy naprężenia o dziewięciu składowych naprężenia. Na rys. 6.37 przedstawiono przykładowo składowe naprężeń działające na płaszczyznę prostopadłą do osi z.
Pierwsza litera indeksu wskazuje płaszczyznę, w której rozpatrywane jest naprężenie. Druga oznacza oś, do której jest równoległy kierunek działania naprężenia stycznego. Z warunku równowagi elementarnej objętości cieczy wynika, że naprężenia te muszą być symetryczne, tzn.
txy = txy; txz = tzx; tyz = tzy. (6.57)

Wszystkie trzy składowe naprężeń działają stycznie do odpowiednich powierzchni.
    Rys. 6.37. Składowe naprężeń stycznych w płaszczyźnie prostopadłej do osi z

Ciśnienie p jest równe średniej trzech składowych naprężeń działających normalnie do odpowiadających im powierzchni
txx + tyy + tzz = -3 p (6.58)

Znak minus oznacza, że za ujemne przyjęto naprężenia ściskające, zaś za dodatnie naprężenia rozciągające.
Wartość naprężeń zależy od odkształcenia cieczy. Dla większości cieczy zależność taka ma następującą postać
tij = h ( ∂ ui
∂ xi		+ ∂ uj
∂ xj		 ) - δij p (6.59)

gdzie: u - składowe wektora prędkości; wyrażenie w nawiasie opisuje odkształcenie cieczy.

Z równania tego wynika, że składowe naprężeń są proporcjonalne do odkształcenia cieczy, przy czym współczynnikiem proporcjonalności jest lepkość dynamiczna h.
Delta Kroneckera ( δij )wskazuje, że p jest odejmowane w przypadku, gdy obydwa indeksy (ij) są jednakowe. Oznacza to, że dodatkowy składnik naprężenia, wynikający z działania statycznego ciśnienia cieczy p, jest odejmowany od naprężeń txx, tyy, tzz. Odpowiednie zależności mają więc następującą postać
txy = h ( ∂ u
∂ y		 + ∂ v
∂ x		 ) (6.60)
txz = h ( ∂ u
∂ z		 + ∂ w
∂ x		 )
tyz = h ( ∂ v
∂ z		 + ∂ w
∂ y		 )

oraz
txx = - p + 2 h ∂ u
∂ x		 (6.61)
tyy = - p + 2 h ∂ v
∂ y
tzz = - p + 2 h ∂ w
∂ z

gdzie: u, v, w - składowe prędkości względem osi x, y, z.

Suma składowych
txx + tyy + tzz = -3 p + 2 h ( ∂ u
∂ x		 + ∂ v
∂ y		 + ∂ w
∂ z		 ) = -3 p + 2 Q (6.62)

Wyrażenie w nawiasie jest dywergencją wektora prędkości, która jest miarą wypływu cieczy z każdego punktu, a więc miarą ekspansji cieczy.

Składowe normalne naprężeń mają postać następującą:
sx = - p + l Q + 2 h ∂ u
∂ x		 (6.63)
sy = - p + l Q + 2 h ∂ v
∂ y
sz = - p + l Q + 2 h ∂ w
∂ z

przy czym lepkość objętościowa l cieczy nieściśliwej zależy od lepkości dynamicznej, co można wyrazić zależnością
l = - 2
3		 h

Dla uogólnienia rozważań założono, że ciecz charakteryzuje się ściśliwością i w takim przypadku
l + 2
3		 h ≠ 0

Składowe przyspieszenia jakiemu podlega element cieczy są określone pochodnymi (d u/d t), (d v/d t), (d w/d t). Ponieważ masa elementu cieczy o wymiarach d x, d y, d z wynosi r d xd yd z (gdzie r - gęstość cieczy), więc składowe siły potrzebnej do nadania przyspieszenia cieczy są następujące
r d u
d t		 d x d y d z (6.64)
r d v
d t		 d x d y d z
r d w
d t		 d x d y d z

Przyspieszenia (d u/d t), (d v/d t), (d w/d t) w stosowane) tutaj metodzie analizy lokalnej (metodzie Eulera) określa się jako pochodne zupełne prędkości względem czasu
d u
d t		 = ∂ u
∂ x		 ∂ x
∂ t		 + ∂ u
∂ y		 ∂ y
∂ t		 + ∂ u
∂ z		 ∂ z
∂ t		 + ∂ u
∂ t		 = u ∂ u
∂ x		 + v ∂ u
∂ y		 + w ∂ u
∂ z		 + ∂ u
∂ t		 (6.65)
d v
d t		 = ∂ v
∂ x		 ∂ x
∂ t		 + ∂ v
∂ y		 ∂ y
∂ t		 + ∂ v
∂ z		 ∂ z
∂ t		 + ∂ u
∂ t
d w
d t		 = ∂ w
∂ x		 ∂ x
∂ t		 + ∂ w
∂ y		 ∂ y
∂ t		 + ∂ w
∂ z		 ∂ z
∂ t		 + ∂ w
∂ t

Ta pochodna zupełna (pochodna substancjalna składa się z dwu części: pochodnej lokalnej ∂ /∂ t przedstawiającej zmiany, jakie zachodzą w danym punkcie pola po upływie czasu d t, oraz pochodnej konwekcyjnej u∂ /∂ t + v∂ /∂ t + w∂ /∂ t ujmującej zmiany, jakie zachodzą przy przesunięciu elementu płynu z punktu (x, y, z ) do punktu (x+ d x, y + d y, z + dz )

Siły potrzebne do nadania przyspieszenia elementowi cieczy pochodzą od pola sił zewnętrznych (grawitacja, siły magnetyczne i in.), ciśnienia lub gradientu naprężeń w cieczy. Jeżeli składowe zewnętrznego pola sił przypadające na jednostkę masy oznacza się przez X, Y, Z to siły te będą równe odpowiednio
X r d x d y d z; Y r d x d y d z; Z r d x d y d z (6.65)

Do sił zewnętrznych należy dodać siły pochodzące od gradientu naprężeń. Dla przykładu element cieczy ma tendencję przemieszczania w kierunku osi x pod wpływem trzech naprężeń sx, txy, txz. Zmiana naprężenia txy, wynikająca ze zmiany odległości o d y, wynosi
∂ txy
∂ y		 d y (6.67)

Naprężenie to działa na powierzchni równej d x d z z siłą równą
∂ txy
∂ y		 d y d x d z (6.68)

Podobnie można wyznaczyć wyrażenia na txx, txz

Dodając siły pochodzące od gradientu naprężeń do sił zewnętrznych oraz upraszczając przez wspólny czynnik d x d y d z otrzymuje się zależność między gradientami naprężeń a przemieszczeniem elementu w kierunku osi x
r d u
d t		 = r X + ∂ sx
∂ x		 + ∂ txy
∂ y		 + ∂ txz
∂ z 		(6.69)

oraz analogicznie w kierunku osi y oraz z
r d v
d t		 = r Y + ∂ txy
∂ x		 + ∂ sy
∂ y		 + ∂ tyz
∂ z 		(6.70)
r d w
d t		 = r Z + ∂ txz
∂ x		 + ∂ tyz
∂ y		 + ∂ sz
∂ z

Po podstawieniu do równań (6.69) i (6.70) zależności (6.60) i (6.63), wiążących naprężenia z odkształceniami, uzyskuje się ogólne równania Naviera-Stokesa
r d u
d t		 = r X - ∂ p
∂ x		 + ∂
∂ x		 [ 2 h ∂ u
∂ x		 + l ( ∂ u
∂ x		 + ∂ v
∂ y		 + ∂ w
∂ z		 ) ] +
(6.71a)
+ ∂
∂ y		 [ h ( ∂ u
∂ y		 + ∂ v
∂ x		 ) ] + ∂
∂ z		 [ h ( ∂ w
∂ x		 + ∂ u
∂ z		 ) ]

r d v
d t		 = r Y - ∂ p
∂ y		 + ∂
∂ y		 [ 2 h ∂ v
∂ y		 + l ( ∂ u
∂ x		 + ∂ v
∂ y		 + ∂ w
∂ z		 ) ] +
(6.71b)
+ ∂
∂ z		 [ h ( ∂ v
∂ z		 + ∂ w
∂ y		 ) ] + ∂
∂ x		 [ h ( ∂ u
∂ y		 + ∂ v
∂ x		 ) ]

r d w
d t		 = r Z - ∂ p
∂ z		 + ∂
∂ z		 [ 2 h ∂ w
∂ z		 + l ( ∂ u
∂ x		 + ∂ v
∂ y		 + ∂ w
∂ z		 ) ] +
(6.71c)
+ ∂
∂ x		 [ h ( ∂ w
∂ x		 + ∂ u
∂ z		 ) ] + ∂
∂ y		 [ h ( ∂ v
∂ z		 + ∂ w
∂ y		 ) ]

Równania zawierają cztery niewiadome u, v, w i p. Czwartym równaniem, umożliwiającym wyznaczenie niewiadomych, jest równanie ciągłości strugi
d r
d t		 + ∂ (r u)
∂ x		 + ∂ (r v)
∂ y		 + ∂ (r w)
∂ z		 = 4 p r m (6.72)

w którym m uwzględnia istnienie dodatnich źródeł przepływu i upustów (źródeł ujemnych). W przypadku ich nieobecności oraz przy założeniu stałości stanu cieczy, równanie to przyjmuje postać
∂ (r u)
∂ x		 + ∂ (r v)
∂ y		 + ∂ (r w)
∂ z		 = 0 (6.73)

Oba równania zawierają oprócz zmienionych u, v, w i p również gęstość r i lepkość h cieczy. Ponieważ r i h są również pewnymi funkcjami, dlatego też dla pełnego sformułowania zagadnienia należy założyć
r = r ( p , T ) ; h = h ( p , T ) .

6.4.2. Uogólnione równanie Reynoldsa

Równanie różniczkowe Reynoldsa w oryginalnej postaci obowiązywało dla cieczy nieściśliwej. Obecnie przedstawione zostanie tzw. uogólnione równanie Reynoldsa uwzględniające wpływ ściśliwości i obciążeń dynamicznych. Podane zostaną też zastosowania tego równania dla poruszających się względem siebie powierzchni łożyska ślizgowego.
    Rys. 6.38. Przekrój warstwy oleju powstającej miedzy dwiema przemieszczającymi się względem siebie powierzchniami; h - grubość warstwy

Założenia sprowadzające równania (6.71) do równania Reynoldsa przy rozpatrywaniu warstwy oleju (rys. 6.38) są następujące:
1) grubość warstwy oleju y = h jest mała w porównaniu z pozostałymi jej wymiarami x, z, założenie to pozwala zaniedbać krzywiznę powierzchni (np. w przypadku poprzecznego łożyska ślizgowego) i rozważać prędkość postępową zamiast prędkości obrotowej,
2) ciśnienie jest tylko funkcją x oraz z, tzn.
∂ p
∂ y		 = 0 (6.74)

3) przepływ jest laminarny, ciągły bez kawitacji, nie ma wirów ani turbulencji;
4) na warstwę oleju nie działają żadne zewnętrzne siły, tzn.
X = Y = Z = 0

5) siły bezwładności są małe w porównaniu z siłami ścinania; pomija się więc siły przyspieszające ruch cieczy, siły odśrodkowe w łożyskach poprzecznych i grawitację cieczy
d u
d t		 = d v
d t		 = d w
d t		 = 0 (6.75)

6) prędkość warstw cieczy bezpośrednio przylegających do powierzchni jest równa prędkości powierzchni;
7) w porównaniu z gradientami prędkości (∂ u / ∂ y) oraz (∂ w / ∂ y) pozostałe gradienty są pomijalnie małe; wynika to z faktu, że u oraz w są prędkościami dominującymi, zaś y jest wymiarem małym w porównaniu z wymiarami x i z (gradienty (∂ u / ∂ y) oraz (∂ w / ∂ y) są związane ze ścinaniem, natomiast pozostałe gradienty - z przyspieszeniami);
8) lepkość i gęstość cieczy nie zależą od współrzędnej y
∂ h
∂ y		 = 0 ; ∂ r
∂ y		 = 0 .

Założenia powyższe sprowadzają równania Naviera-Stokesa do układu równań
1
h		 ∂ p
∂ x		 = ∂ ² u
∂ y ² 		; 1
h		 ∂ p
∂ z		 = ∂ ² w
∂ y ²		 (6.76)

Równania można otrzymać także na podstawie równań równowagi sił działających na element cieczy wyodrębniony z warstwy oleju.
Przy zaniedbaniu sił zewnętrznych i sił bezwładności oraz gradientu ciśnienia w kierunku osi y, pozostają jedynie siły styczne i normalne przedstawione na rys. 6.39.
Równania równowagi rzutów sił na oś x iż mają następującą postać
( tx + ∂ tx
∂ z		 dz ) dx dy - tx dx dy + ( tx + ∂ tx
∂ y		 dy ) dx dz - tx dx dz +
(6.77a)
+ ( p -½ ∂ p
∂ x		 dx ) dy dz - ( p + ½ ∂ p
∂ x		 dx ) dy dz = 0
    Rys. 6.39. Siły działające na elementarną objętość cieczy:
    a) w kierunku osi x,
    b) w kierunku osi z

( tz + ∂ tz
∂ x		 dx ) dy dz - tz dy dz + ( tz + ∂ tz
∂ y		 dy ) dx dz - tz dx dz +
(6.77b)
+ ( p -½ ∂ p
∂ z		 dz ) dx dy - ( p + ½ ∂ p
∂ z		 dz ) dx dy = 0
zaś po uporządkowaniu i zredukowaniu
∂ tx
∂ y 		+ ∂ tx
∂ z 		= ∂ p
∂ x 		(6.78)
∂ tz
∂ y 		+ ∂ tz
∂ x 		= ∂ p
∂ z

Zakładając, że mamy do czynienia z cieczą newtonowską, a więc cieczą w której naprężenia ścinające są proporcjonalne do gradientu ścinania, czyli
tx = h ∂ u
∂ y 		(6.79)
tz = h ∂ w
∂ y

i podstawiając do równania (6.78), otrzymuje się następującą postać równań równowagi
∂ ² u
∂ y ²		 + ∂ ² u
∂ y ∂ z		 = 1
h		 ∂ p
∂ x 		(6.80)
∂ ² w
∂ y ²		 + ∂ ² w
∂ x ∂ y		 = 1
h		 ∂ p
∂ z

Równania te oznaczają, że lepkość jest niezależna od gradientu ścinania, co nie jest niestety słuszne dla wszystkich cieczy. Po uwzględnieniu założenia, że w porównaniu z gradientami (∂ u/∂ y) i (∂ w/∂ y) pozostałe gradienty są pomijalnie małe równania równowagi (6.80) przybierają postać identyczną z równaniami uzyskanymi po uproszczeniu równania Naviera-Stokesa
∂ ² u
∂ y ²		 = 1
h		 ∂ p
∂ x 		(6.81a)
∂ ² w
∂ y ²		 = 1
h		 ∂ p
∂ z 		(6.81b)

Całkując równanie (6.81a) oraz korzystając z warunków brzegowych
u = U1 dla y = 0 ; u = U2 dla y = h

otrzymuje się
u = 1
2 h		 ∂ p
∂ x		 y ( y - h ) + h - y
h		 U1 + y
h		 U2 (6.82)

Całkując równanie (6.81b) oraz korzystając z warunków brzegowych:
w = 0 dla y = 0 ; w = 0 dla y = h

co oznacza, że ruch powierzchni łożyska odbywa się jedynie w kierunku osi x, otrzymuje się
w = 1
2 h		 ∂ p
∂ z		 y ( y - h ) (6.83)

Równania (6.82) i (6.83) opisują rozkład prędkości w funkcji lepkości h, kształtu warstwy oleju h, prędkości powierzchni U1 i U2 oraz gradientów ciśnienia.

Dalszy ciąg rozważań dotyczy równania ciągłości strugi, które można przedstawić w następujący sposób
∂ (r v)
∂ y		 = - ∂ (r u)
∂ y		 - ∂ (r w)
∂ z 		(6.84)

Podstawiając wyznaczone zależności na u i w otrzymuje się
(6.85)

Całkując względem y w granicach od O do h można napisać
(6.86)

Górna granica całkowania h w ostatnim równaniu jest funkcją x oraz z, tzn. h = h (x, z) .

Dla dalszych przekształceń należy skorzystać z następującej zależności
(6.87)

Po uwzględnieniu w równaniu (6.86) wzoru (6.87) oraz wykorzystaniu warunków brzegowych
v = 0 dla y = 0 i v = V dla y = h
otrzyma się
(6.88)

albo
∂
∂ x		 ( r h³
h		 ∂ p
∂ x		 )+ ∂
∂ z		 ( r h³
h		 ∂ p
∂ z		 ) = 6 (U1 - U2) ∂ (r h)
∂ x		 6 r h ∂
∂ x		 (U1 + U2) + 12 r V (6.89)

W warunkach dynamicznego obciążenia, kiedy istnieje składowa prędkość V, prędkości styczne U mogą się zmieniać.

Dla łożyska z wirującym czopem i nieruchomą panewką mamy
U = R w1 + c d e
d t		 sin q - c e d (b + g )
d t		 cos q
V = c d e
d t		 cos q + c e d (b + g )
d t		 sin q
(6.90)

gdzie: R - promień czopa w m, w1 - prędkość kątowa czopa w s-1, c - luz promieniowy w m, e=e/c - mimośrodowość względna, kąty występujące w zależnościach 6.90 pokazano na rys. 6.54.

Różniczkując U względem x
∂ U
∂ x		 = 1
R		 ∂ U
∂ q		 = 1
R		 c [ d e
d q		 cos q + c e d (b + g )
d t		 sin q ] 1
R		 V (6.91)

zatem
6 r h ∂
∂ x		 (U1 + U2) + 12 r V = 12 r h
R		 V + 12 rV = 12 r ( 1 + h
R		 ) V (6.92)

Ponieważ wyrażenie h/R << 1 (generalnie rzędu 0,001), dlatego też można je zaniedbać. Równanie Reynoldsa (6.89) przyjmuje więc następującą postać
∂
∂ x		 ( r h³
h		 ∂ p
∂ x		 )+ ∂
∂ z		 ( r h³
h		 ∂ p
∂ z		 ) = 6 (U1 - U2) ∂ (r h)
∂ x		 + 12 r V (6.93)

Wyrażenie 6(U1 - U2) ∂ r h/∂ x opisuje wpływ prędkości stycznych łożyska na zmianę ciśnienia w warstwie oleju, zaś wyrażenie 12r V, zmiany ciśnienia wynikające z istnienia składowej normalnej V prędkości pochodzącej od obciążeń dynamicznych. Podstawa dalszej dyskusji będzie nieco zmieniona, wynikająca z założenia stałej gęstości r, a więc równanie (6.93) przyjmie postać
∂
∂ x		 ( h³
h		 ∂ p
∂ x		 )+ ∂
∂ z		 ( h³
h		 ∂ p
∂ z		 ) = 6 (U1 - U2) ∂ h
∂ x		 + 12 V (6.94)

Należy zauważyć, że wpływ wyrażenia (U1 - U2)∂ h/∂ x zależy od tego, czy powierzchnie łożyska mają prędkości postępowe, czy obwodowe.
    Rys. 6.40. Przykład ruchu względnego dwóch powierzchni:
    a) łożyska wzdłużnego,
    b) łożyska poprzecznego

W przypadku ślizgacza wzdłużnego, jeżeli U1 = U2 = U (rys. 6.40), to pierwszy człon prawej strony równania (6.94) przyjmuje wartość równą zeru. Jeżeli dodatkowo założyć brak ruchu normalnego (V = 0), to łożysko takie nie ma żadnej zdolności przenoszenia obciążeń. Odwrotnie, jeżeli U1 = -U2 wówczas obciążalność łożyska jest dwukrotnie większa niż w przypadku, gdy jedna z powierzchni jest nieruchoma.
W łożysku poprzecznym, jeżeli U1 = U2 = U to człon pierwszej prawej strony równania (6.94) przyjmuje także wartość równą zeru. Ruch obrotowy powierzchni sprawia, że występują obydwie składowe prędkości: styczna i normalna. Zgodnie z rys. 6.40 wynoszą one odpowiednio: składowa styczna prędkości = U cos a ≈ U, składowa normalna prędkości = U sin a ≈ U = tg a = U ∂ h/∂ x = V . W takim przypadku prawa strona równania (6.94) przyjmuje postać 2U ∂ h/∂ x co implikuje dwukrotny wzrost obciążalności, w porównaniu z łożyskiem o nieruchomej panewce (U1 = 0 ). Odwrotnie, jeżeli powierzchnie łożyska przemieszczają się w przeciwnych kierunkach, tzn. U1 = - U2 to pierwszy człon prawej części równania (6.94) przyjmuje postać 2U ∂ h/∂ x, znak V zmienia się na przeciwny, co daje -2U ∂ h/∂ x. Łożysko takie nie ma więc żadnej zdolności przenoszenia obciążeń (prawa strona równania = 2U ∂ h/∂ x - 2U ∂ h/∂ x = 0). Opisane zjawiska łatwo wytłumaczyć intuicyjnie pamiętając o różnicach jakie istnieją między przemieszczaniem powierzchni łożyska wzdłużnego, a przemieszczaniem łożyska poprzecznego. Zakładając równość prędkości obydwu powierzchni łatwo wykazać, że dwa dowolnie wybrane punkty A, B (rys. 6.40) leżące na przeciwległych powierzchniach łożyska wzdłużnego, zachowują stałą odległość pomimo ruchu powierzchni, do których należą. Inaczej zachowują się dwa podobnie wybrane punkty czopa i panewki łożyska poprzecznego. Zbliżają się one do siebie z prędkością poruszających się powierzchni.
Równanie Reynoldsa (6.93) jest niejednorodnym równaniem różniczkowym dwu zmiennych o pochodnych cząstkowych. Jest to równanie trudne do rozwiązania, przy czym stopień jego złożoności zależy od funkcji h = h ( x, z), h = h( x, z) oraz od warunków brzegowych. Nawet najprostszy przypadek h oraz h = const a V = 0 redukujący równanie (6.93) do postaci
∂
∂ x		 ( h³ ∂ p
∂ x		 )+ ∂
∂ z		 ( h³ ∂ p
∂ z		 ) = 6 h (U1 - U2) ∂ h
∂ x		 (6.95)

jest trudny do rozwiązania. W dalszych rozważaniach przedstawione będą przykłady rozwiązań równania Reynoldsa dla prostych postaci funkcji h ( x), gdy oś czopa i panewki są równoległe, czyli ∂ h/∂ x = 0.

W równaniu (6.93) V reprezentuje wypadkową prędkość normalną bez rozróżnienia przyczyn ruchu w kierunku promieniowym. W łożysku wzdłużnym prędkość V pochodzi jedynie od normalnego przemieszczenia poruszających się powierzchni. W łożysku poprzecznym prędkość normalna V może pochodzić zarówno od wzajemnego przemieszczania powierzchni łożyska na skutek ruchu obrotowego, jak też na skutek ruchu środka czopa.
Wygodnie jest przyjąć, że w równaniu (6.95) V przedstawia jedynie prędkość pochodzącą od ruchu środka czopa. Zgodnie zatem z rozważaniami przeprowadzonymi poprzednio, na podstawie równania (6.92), należy drugi człon prawej strony równania (6.93) uzupełnić o wyrażenie U2 ∂ r h/∂ x. Zatem
∂
∂ x		 ( r h³
h		 ∂ p
∂ x		 )+ ∂
∂ z		 ( r h³
h		 ∂ p
∂ z		 ) = 6 (U1 - U2) ∂ (r h)
∂ x		 + 12 [ U2 ∂ (r h)
∂ x		 +r Vo] (6.96)

albo
∂
∂ x		 ( r h³
h		 ∂ p
∂ x		 )+ ∂
∂ z		 ( r h³
h		 ∂ p
∂ z		 ) = 6 (U2 + U1) ∂ (r h)
∂ x		 + 12 r Vo (6.97)
gdzie Vo prędkość ruchu środka czopa.

W większości praktycznych przypadków element nośny (w łożysku poprzecznym - panewka) jest nieruchomy. W łożysku wzdłużnym przemieszcza się na ogół ślizgacz, zaś w łożysku poprzecznym czop.
W takich przypadkach równanie (6.97) redukuje się do postaci słusznej dla łożysk wzdłużnych i poprzecznych
∂
∂ x		 ( r h³
h		 ∂ p
∂ x		 )+ ∂
∂ z		 ( r h³
h		 ∂ p
∂ z		 ) = 6 U ∂ (r h)
∂ x		 + 12 r Vo (6.98)

Dla łożysk statycznie obciążonych (Vo) smarowanych cieczą nieściśliwą (r = const ) równanie (6.98) przybiera najbardziej rozpowszechnioną postać równania Reynoldsa
∂
∂ x		 ( h³
h		 ∂ p
∂ x		 )+ ∂
∂ z		 ( h³
h		 ∂ p
∂ z		 ) = 6 U ∂ h
∂ x 		(6.99)

6.4.3. Równania przepływu i ścinania

Rozwiązanie równania Reynoldsa doprowadziło do sformułowania wielu użytecznych z punktu widzenia teorii smarowania wyrażeń. Należą do nich m.in. równania przepływu i ścinania. Jak wykazano uprzednio, równania (6.82) i (6.83) opisują składowe prędkości smaru w kierunku osi x oraz z. Przez ich scałkowanie w granicach od 0 do h, a więc w obszarze pomiędzy powierzchniami łożyska uzyskuje się wyrażenia na natężenie przepływu
(6.100)

(6.101)

Przepływ w kierunku osi z może być dodatni lub ujemny w zależności od znaku gradientu ciśnienia. Przepływ w kierunku osi x odbywa się pod wpływem dwóch czynników: wynikającego z gradientu ciśnienia (h³/12 h)( ∂ p/∂ x) oraz wynikającego ze ścinania &frac=12;h (U1 + U2). Jego kierunek zależy od wartości U1 i U2 oraz od znaku ( ∂ p/∂ x) .
Naprężenia ścinające dla cieczy newtonowskiej są określone za pomocą równania
tx = h ∂ u
∂ y		 ; tz = h ∂ w
∂ y 		(6.102)

Różniczkując równania (6.82) i (6.83) względem y, otrzymuje się
∂ u
∂ y		 = 1
2 h		 ∂ p
∂ x		 (2 y - h) + 1
h		 (U2 - U1)

∂ w
∂ y		 = 1
2 h		 ∂ p
∂ z		 (2 y - h)

Zatem
tx = 1
2 h		 ∂ p
∂ x		 (2 y - h) + h
h		 (U2 - U1) (6.103a)

tz = 1
2 h		 ∂ p
∂ z		 (2 y - h) (6.103b)

Wartość naprężeń ścinających zależy od y oraz h. Dla powierzchni poruszającej się z prędkością U1 współrzędna y = 0, czyli
tx = h
2		 ∂ p
∂ x		 + h
h		 (U2 - U1) (6.104a)

tz = - h
2		 ∂ p
∂ z 		(6.104b)

Dla powierzchni poruszającej się z prędkością U2. współrzędna y = h
tx = h
2		 ∂ p
∂ x		 + h
h		 (U2 - U1) (6.105)
tz = h
2		 ∂ p
∂ z

Całkowitą siłę oporów stycznych można otrzymać przez całkowanie t po całej powierzchni łożyska
T = ∫ ∫ t d S (6.106)

Ponieważ siła styczna Tz jest prostopadła do kierunku przemieszczania powierzchni łożyska, całkowity opór dla y = 0 lub y = h wyraża się wzorem
(6.107)

przy czym znak plus dla czopa ( y = h ), minus - dla panewki ( y = 0 ).
Równanie to przedstawione we współrzędnych walcowych umożliwia obliczenie momentu oporu
(6.108)

6.4.4. Równanie energii

Przeprowadzenie dokładnej analizy działania łożyska wymaga uwzględnienia zależności lepkości oleju od temperatury. Ścinanie cieczy oznacza, że wykonana praca tarcia wewnętrznego zmienia się w ciepło. Powstający w ten sposób wzrost temperatury zmniejsza lepkość cieczy nieściśliwej i zwiększa lepkość cieczy ściśliwej. Zmiany lepkości należy uwzględnić w równaniu Reynoldsa, które przewiduje w swej ogólnej postaci funkcję h( T ).
W ten sam sposób, rozważając przenoszenie ciepła i odkształcenia termiczne, można określić istniejące w łożysku gradienty temperatury. Elementarna objętość o wymiarach Dx, Dy, Dz przedstawiona na rys. 6.41 zawiera ciecz, której
    Rys. 6.41. Parametry zmienne charakteryzujące elementarną objętość cieczy

parametry prędkości u, v, w temperatura T, ciśnienie y, gęstość r i lepkość h są zmienne. Z pierwszej zasady termodynamiki wynika, że suma energii przypadającej na jednostkę objętości w rozważanym przedziale czasu wyraża się następująco
Ei + Hdo = Es + Ec - Hdb (6.109)

gdzie: Hdo - praca wykonana nad cieczą przez otoczenie. Ei - energia dostarczona do elementarnej objętości. Es -energia chwilowo zmagazynowana w elementarnej objętości, Eo - energia odbierana z elementarnej objętości. Hdb - praca wykonana przez ciecz nad otoczeniem.

W warunkach ustalonych równanie to przyjmuje postać
Eo - Ei = Hdo - Hdb (6.110)

Dostarczanie lub odbieranie energii z elementarnej objętości może odbywać się przez przewodzenie, zgodnie z prawem Fouriera, oraz przez konwekcję energii strumienia cieczy. Wpływ promieniowania jest w dalszych rozważaniach pominięty. Pozostałe rodzaje energii występujące w bilansie energii pochodzą z pracy mechanicznej, wykonanej przez naprężenia (∂ t) występujące w cieczy oraz przez siły masowe na elementarnej odległości w jednostce czasu. Z punktu widzenia rozważanego tu procesu smarowania siły masowe można pominąć.

Wymienione wyżej strumienie energii oraz prace mechaniczne można określić dla wydzielonej elementarnej objętości cieczy (rys. 6.42). Dla przejrzystości naniesiono na rysunku jedynie wybrane wielkości. Należy zauważyć, że zmiany energii przedstawiono w stosunku do punktu środkowego O elementarnej objętości cieczy.
Na podstawie rys. 6.42 można obliczyć lewą stronę równania (6.110)
Eo - Ei = { [ ∂ (r ue)
∂ x		 + ∂ (r ve)
∂ y		 + ∂ (r we)
∂ z		 ] +
- [ ∂
∂ x		 ( k ∂ T
∂ x		 ) + ∂
∂ y		 ( k ∂ T
∂ y		 ) + ∂
∂ z		 ( k ∂ T
∂ z		 ) ] } D x D y D z
(6.111)

    Rys. 6.42. Wielkości opisujące strumień energii i prac mechanicznych wykonanych nad i przez elementarną objętość cieczy

zaś energia strumienia cieczy
e = u² + v² + w²
2		 (6.112)
gdzie: k - przewodność cieplna w W/(m • K), cv - ciepło właściwe przy stałej objętości w J/(kg • K), T - temperatura w K.

Podobnie należy zsumować prace mechaniczne przy założeniu, że wszystkie prace wykonane nad i przez elementarną objętość cieczy są spowodowane oddziaływaniem w płaszczyznach, w których składowe prędkości są skierowane przeciwnie do odpowiednich składowych naprężeń. Prawa strona równania (6.110) ma więc następującą postać
Hdo - Hdb = [ ∂
∂ x		 (usx + vtyx + wtzx) + ∂
∂ y		 (utxy + vsy + wszy) +
+ ∂
∂ z		 (utxz + vtyz + wsz) ] D x D y D z
(6.113)

Porównując wyznaczone wyrażenia na E i H zgodnie z równaniem (6.110) oraz równaniami (6.111) i (6.113) otrzymamy
[ ∂ (r ue)
∂ x		 + ∂ (r ve)
∂ y		 + ∂ (r we)
∂ z		 ] - [ ∂
∂ x		 ( k ∂ T
∂ x		 ) +
+ ∂
∂ y		 ( k ∂ T
∂ y		 ) + ∂
∂ z		 ( k ∂ T
∂ z		 ) ] = ∂
∂ x		 (usx + vtyx + wtzx) +
+ ∂
∂ y		 (utxy + vsy + wszy) + ∂
∂ z		 (utxz + vtyz + wsz) (6.114)

skąd uzyskuje się
r ( u ∂ e
∂ x		 + v ∂ e
∂ y		 + w ∂ e
∂ z		 ) - [ ∂
∂ x		 ( k ∂ T
∂ x		 ) + ∂
∂ y		 ( k ∂ T
∂ y		 ) + ∂
∂ z		 ( k ∂ T
∂ z		 ) ] =
= u ( ∂ sx
∂ x		 + ∂ txy
∂ y		 + ∂ txz
∂ z		 ) + v ( ∂ tyx
∂ x		 + ∂ sy
∂ y		 + ∂ tyz
∂ z		 ) +
+ w ( ∂ tzx
∂ x		 + ∂ tzy
∂ y		 + ∂ sz
∂ z		 ) + ( sx ∂ u
∂ x		 + sy ∂ v
∂ y		 + sz ∂ w
∂ z		 ) +
+ txy ( ∂ u
∂ y		 + ∂ v
∂ x		 ) + tyz ( ∂ v
∂ z		 + ∂ w
∂ y		 ) + tzx ( ∂ w
∂ x		 + ∂ u
∂ z		 )
(6.115)

Pierwszy człon lewej strony równania (6.114) po zastosowaniu równania ciągłości strugi
∂ (r u)
∂ x		 + ∂ (r v)
∂ y		 + ∂ (r w)
∂ z		 = 0 (6.116)

zredukowany został do postaci
r ( u ∂ e
∂ x		 + v ∂ e
∂ y		 + w ∂ e
∂ z		 )

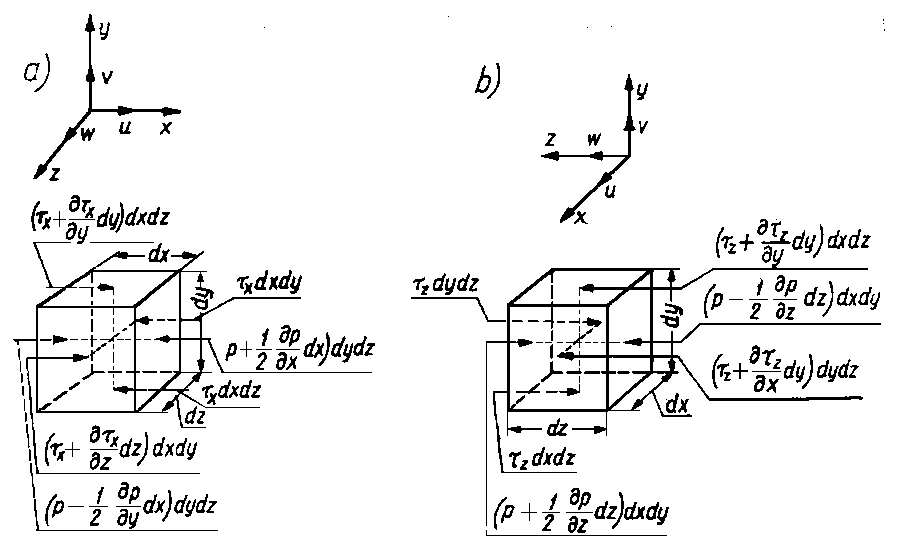
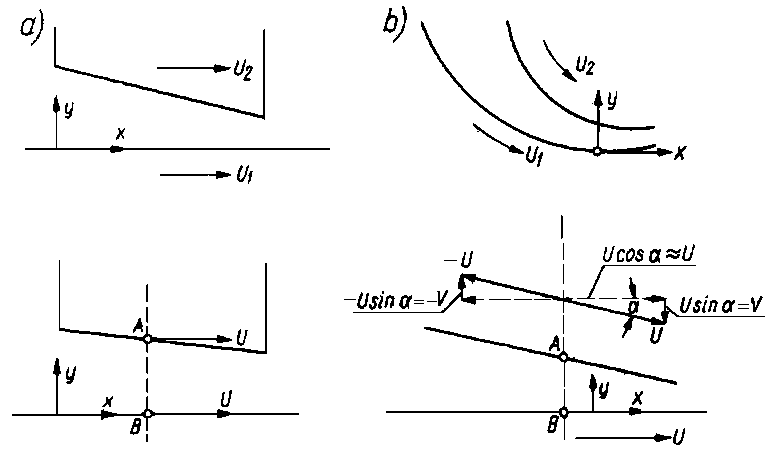
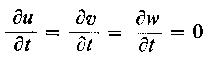Przytoczone uprzednio równania równowagi przepływu cieczy, które posłużyły do wyprowadzenia równań Naviera-Stokesa, po uwzględnieniu warunku oraz zaniedbaniu sił masowych przyjmują następującą postać
r ( u ∂ u
∂ x		 + v ∂ u
∂ y		 + w ∂ u
∂ z		 ) = ∂ sx
∂ x		 + ∂ txy
∂ y		 + ∂ txz
∂ z 		(6.117a)

r ( u ∂ v
∂ x		 + v ∂ v
∂ y		 + w ∂ v
∂ z		 ) = ∂ tyx
∂ x		 + ∂ sy
∂ y		 + ∂ tyz
∂ z 		(6.117b)

r ( u ∂ w
∂ x		 + v ∂ w
∂ y		 + w ∂ w
∂ z		 ) = ∂ tzx
∂ x		 + ∂ tzy
∂ y		 + ∂ sz
∂ z 		(6.117c)

Równania Naviera-Stokesa powstały przez podstawienie do powyższych równań wyrażeń na s oraz t. Przez podstawienie wyżej wymienionych trzech równań oraz wyrażeń na s i t do równań (6.115) otrzymuje się
r ( u ∂ e
∂ x		 + v ∂ e
∂ y		 + w ∂ e
∂ z		 ) - [ ∂
∂ x		 ( k ∂ T
∂ x		 ) + ∂
∂ y		 ( k ∂ T
∂ y		 ) + ∂
∂ z		 ( k ∂ T
∂ z		 ) ] =
= r [ u ∂
∂ x		 ( u² + v² + w²
2		 ) + v ∂
∂ y		 ( u² + v² + w²
2		 ) +
+ w ∂
∂ z		 ( u² + v² + w²
2		 ) - p ( ∂ u
∂ x		 + ∂ v
∂ y		 + ∂ w
∂ z		 ) + F (6.118)

Z kolei podstawiając
e = u² + v² + w²
2		 + cv T (6.119)

otrzymuje się
r [ u ∂ (cv T)
∂ x		 + v ∂ (cv T)
∂ y		 + w ∂ (cv T)
∂ z		 ] + p [ ∂ u
∂ x		 + ∂ v
∂ y		 + ∂ w
∂ z		 ] =
= [ ∂
∂ x		 ( k ∂ T
∂ x		 ) + ∂
∂ y		 ( k ∂ T
∂ y		 ) + ∂
∂ z		 ( k ∂ T
∂ z		 ) ] +F
(6.120)

przy czym
F = h [ 2 ( ∂ u
∂ x		 )² + 2 ( ∂ v
∂ y		 )² + 2 ( ∂ w
∂ z		 )² - 2
3		 ( ∂ u
∂ x		 + ∂ v
∂ y		 + ∂ w
∂ z		 )² +
+( ∂ u
∂ y		 + ∂ v
∂ x		 )² + ( ∂ v
∂ z		 + ∂ w
∂ y		 )² + ( ∂ w
∂ x		 + ∂ u
∂ z		 )² ] (6.121)

Wyrażenie w pierwszym nawiasie kwadratowym lewej strony równania (6.120) opisuje konwekcję energii wewnętrznej cieczy. Wyrażenie w drugim nawiasie kwadratowym opisuje pracę, jaką wykonują poszczególne elementy cieczy przy pokonywaniu oporów ciśnienia otaczających warstw.
Wyrażenie w nawiasie po prawej stronie równania opisuje przewodność cieplną w cieczy, zaś 0 określa dyssypację energii kinetycznej cieczy (zamiana na ciepło).
Całkując równanie energii w granicach od 0 do h (h grubość warstwy oleju) uzyskuje się
[ ( r U h
2		 - h³
12 n		 ∂ p
∂ x		 ) ∂ (cv T)
∂ x		 - h³
12 n		 ∂ p
∂ z		 ∂ (cv T)
∂ z 		] +
- [ ∂
∂ x		 ( h k ∂ T
∂ x		 ) + ∂
∂ z		 ( h k ∂ T
∂ z		 ) ] + KT (T - Tw) =
= r n U²
h		 + h³
12 r n		 [ ( ∂ p
∂ x		 )² + ( ∂ p
∂ z		 )² ] (6.122)

gdzie: n - lepkość kinematyczna w m²/s, KT - sumaryczny współczynnik przejmowania ciepła dla powierzchni międzyfazowych ciecz-ciało stałe w W/(m² • K), Tw - temperatura powierzchni łożyska w K, pozostałe oznaczenia, jak w poprzednich wzorach.

Przewodność cieplna większości olejów stosowanych do smarowania łożysk ślizgowych jest niewielka. Oprócz tego jak wykazano w (6.120) współczynnik przejmowania ciepła dla granicznych powierzchni międzyfazowych olej-ciało stałe jest mały. Należy również oczekiwać, że wzrost temperatury cieczy w warstwie oleju będzie niewielki. Ciepło właściwe cieczy cv można więc przyjąć jako stałe, a przewodność cieplną K i współczynnik przejmowania ciepła KT - równe zeru.
Po uwzględnieniu powyższych warunków, równanie (6.122) przyjmuje następującą postać
6 r cv h [ ( 1 - h²
6 h U		 ∂ p
∂ x		 ) ∂ T
∂ x		 - h²
6 h U		 ∂ p
∂ z		 ∂ T
∂ z		 ] =
= 12 h U²
h		 { 1 + h4
12 h² U²		 [ ( ∂ p
∂ x		 )² + ( ∂ p
∂ z		 )² ] } (6.123)

Z równania (6.123) wynika, że ciepło wytwarzane na skutek lepkościowych oddziaływań w cieczy jest przenoszone na skutek ruchu materii. Nie uwzględnia ono strat i zysków ciepła, które mogą powstawać na powierzchniach czopa i panwi.

Równanie (6.123) można przedstawić także w formie bezwymiarowej, bardziej dogodnej do zastosowania rozwiązań numerycznych. Podstawiając do równania (6.123) zależności
p = p B
6 h1 U		 ; T = T r1cv B
h1 U		 ; x = x
B		 ;
h = h
B		 ; h = h
h1 		; r = r
r1 		(6.124)

otrzymuje się postać bezwymiarową równania energii
r h ( 1 - h²
h		 ∂ p
∂ x		 ) ∂ T
∂ x		 - r h²
h		 ∂ p
∂ z		 ∂ T
∂ z		 ] =
h
h		 { 1 + 3 h4
h²		 [ ( ∂ p
∂ x		 )² + ( ∂ p
∂ z		 )² ] } (6.125)

gdzie B - długość łożyska wzdłuż osi x.

Podobnie, po podstawieniu odpowiednich zależności, można przekształcić równanie Reynoldsa, otrzymując
∂
∂ x		 [ r h ( 1 - h²
h		 ∂ p
∂ x		 ) ] - ∂
∂ z		 ( rh³
h		 ∂ p
∂ z		 ) = 0 (6.126)

6.4.5. Równanie stanu

W równaniu (6.123) lepkość h jest znaną funkcją ciśnienia p oraz temperatury T, zaś grubość warstwy cieczy h jest znaną funkcją x i z. Oznacza to, że
h = h (x, z ); h = h (x, z )

Ponieważ zależność (6.125) zawiera trzy niewiadome (p, r oraz T ), to do ich wyznaczenia jest potrzebne dodatkowe równanie. Równaniem łączącym ze sobą te zmienne jest tzw. równanie stanu gazu
p V = R T (6.127)

gdzie: V - objętość molowa gazu w m³/mol, T - temperatura w K, R - stalą gazowa R = = 8,314 J/(mol- K), p - ciśnienie w Pa.

W przypadku smarowania gazem równanie to dostatecznie dobrze spełnia warunki rzeczywiste. Ponieważ wielkościami o praktycznym znaczeniu są p i T, dlatego też r należy wyrugować z równań (6.125) i (6.126) za pomocą równania (6.127).
Zastosowanie równania stanu do smarowania cieczami jest nieco trudniejsze. Nawet w przypadku cieczy o prostej budowie chemicznej są wymagane poprawki algebraiczne, których wprowadzenie do równania (6.127) komplikuje rozwiązanie i wymaga zastosowania techniki numerycznej.
Jeżeli jest możliwe pominięcie zmian r, h itd. z temperaturą, albo jeżeli zmiany z temperaturą mogą być zastąpione a priori znanymi funkcjami x oraz. z, to równanie (6.126) staje się równaniem o jednej niewiadomej p. Otrzymane rozwiązanie można wtedy podstawić do równania (6.125), które staje się wtedy równaniem jedynie ze względu na jedną niewiadomą T, którą można wtedy z niego wyznaczyć.

    

Literatura

Rozdział 6 i 7. Tarcie płynne i mieszane

  1. Hayward A. T. J.: The Viscosity of Bubbly Oil. J. Inst. Petr. 1962 vol. 48 Mai pp. 156-164
  2. Hafschek E.: The Viscosity of Liquds. London: Bell and Sons 1928
  3. Sobańska K.: Lepkość olejów i ich mieszanek. Technika smarownicza 1972 t. 3 s. 25-32
  4. Vogel H.: Das Temperaturabhangigkeitgesetz der Viskosität von Flüssigkeiten. Physik Z. 1921 B. 22 s. 645-646
  5. Rost W.: Das Viscosität-Temperatur-Verhalten von Flüsigkeiten. Koloid Z. 1955 B. 142 s. 132-150
  6. Erk S., Eck H.: Über die Temperaturabhängigkeit der Zähigkeit von Schmierölen. Physik Z. 1936 B. 37 s. 113-119
  7. Cameron A.: Determination of the Pressure-Viscosity-Coefficient. J. Inst. Petr. 1945 vol. 31 pp. 401-414
  8. Cameron A.: Principles of Lubrication. Longmans Green a not Co London 1966
  9. Rost W.: Das Viskosität-Temperatur-Verhalten von Schmierölen. Erdöl u. Kohle 1955 B. 8 S. 468-473, 549-552, 650-651, 718-722
  10. Rumpf K. K.: Bestimmung der Konstante der Walther-Funktion auf graphischen Wege. Schmierungstechnik 1971 Nr 4 S. 157-161
  11. Rumpf K. K.: Die Abhängigkeit der Viskosität-Temperatur-Steilheitsfunktionen und der Siedepunkte definierter Kohlenwasserstoffe von ihrer Viskosität. Erdöl u. Kohle 1967 B. 20 S. 276--286
  12. Rumpf K. K.: System Visplan. Erdöl u. Erdgas Z. 1969 B. 85 S. 313-321
  13. Pressure - Viscosity Report. Vol. I i II. A Report of the ASME Research Committee on Lubrication New York 1953
  14. Schnurmann R.: Calculating Viscosity Index Between VI = O and VI = 30. J. Inst. Petr. 1966 vol. 52 pp. 312-313
  15. Stech W.: Zur Kennzeiehnung der Temperaturbhängigkeit der Viskosität von Schmierstoffen. Schmiertechnik 1969 B. 16 S. 157-158
  16. Witt K.: Wie weit ermoglichen Messungen von Druck Temperatur und Viskosität bis zu hohen Driicken die Vorausberechnung der Gebrauch-Viskosität? Schmiertechnik 1974 B. 21 S. 145--148
  17. Hätte F.: Analitische Darstellung der Viskosität von Flüssigkeiten abhängig von Temperatur und Drück. Schmiertechnik 1974 B. 21 S. 55-60
  18. Hollinghurst R., Singleton A.: Viscosity and Engine Performance J. Inst. Petr. 1969 vol. 55 pp. 205-218
  19. Denis J., Parc G.: Rheological Limits of Mineral and Synthetic Hydrocarbon Base Stocks. J. Inst. Petr. 1973 vol. 59 pp. 70-83
  20. Stolle H.: Ein Verfahren zur rechnerischen Ermittiung der Mischungsverhältnisse... Erdöl . Kohle 1965 B. 18 S. 801-802
  21. Hememan W., Aaron C.: Kritische Bewertung von Untersuchungs-Methoden für das Kältefließerhalten vor Mitteldestiiaten. Erdöl u. Kohle 1972 B. 25 S. 32-38
  22. Klaus E. E., Johnson R. H., Fresco G. P.: Development of a Precision Capilary - Type - Pressure Viscometer. ASLE Trans. 1966 vol. 9 pp. 114-120.
  23. Chu P. S. Y., Cameron A.: Pressure Viscosity Characteristics of Lubricating Oils. J. Inst. Petr. 1962 vol. 48 pp. 148-155
  24. Horsey M. D., Hopkins R. F.: Viscosity of Lubricants under Pressure Report to ASME Res. Comm. on Lubrication 1954
  25. Noack G.: Zur Erfassung der Viskositäts-Temperatur-Abhängigkeit von Schmierölen durch die Vogelsche Gleichung. Schmiertechnik 1973 B. 20 S. 74-80
  26. Eberan-Eberhorst G. A., Weise E.: Die Bedeutung der Viskositäts-Temperatur-Charakteristik von Ein-und Mehrbereichsmotorenölen im praktischen Betrieb. Erdöl u. Kohle 1973 B. 26 S. 93-101
  27. Kuss E.: Viskosität-Druckverhalten von flüsigen Methyl-Phenyl und Cyclohexylmethyl-Siloxanen. Erdöl u. Kohle 1974 B. 27 S. 416-422
  28. Gottner G. H.: Über die Kenzahlen fiir das Viskositäts-Temperatur-Verhalten von Schmierstoffen. Leipzig 1949
  29. Kuss E.: Hochdruckuntersuchungen. Die Viskosität von Komprimierten Flüssigkeiten. Z. Angew. Phys. 1955 B. 5 S. 372-378
  30. Kuss E.: Zur Frage des Viscositäts-Druckverhaltens von Öl. Erdöl Zeitschrift 1962 B. 78 S. 678-686
  31. Kuss E., Pollmann P.: Viskositäts-Druckabhängigkeit und Verzweigungsgrad flüssiger Alkane. Z. Phys. Chem. 1969 B. 68 S. 205-212
  32. Koelber H., Siemens W., Luther H.: Viskositätseigenschaften als Funktion des Molekulargewichts in homologen Kohlenwasserstoffreihen. Brennstofi. Chem. 1949 B. 30 S. 362-371
  33. Mikeska L. A.: Chemical Structure of Lubricating Oils. Ind. Eng. Chem. 1936 vol. 28 pp. 970-984
  34. Luther H.: Die Viscosität reiner Kohlenwasserstoffe. Angew. Chemie 1949 A-61 S. 405-406
  35. Dean E., Davis G. H. B.: Viscosity Variations of Oils with Temperature. Chem. and Met. Eng. 1929 vol. 36 pp. 618-619
  36. Hardiman E., Nissan A. H.: A Rational Basis for the Viscosity index System. Journ. Inst. Petr. 1945 vol. 31 pp. 255-270
  37. Ramser J. H.: Representation of Viscosity-Temperature Characteries of Lubrication Oils. Ind. Eng. Chem. 1949 vol. 41 pp. 3053-2059
  38. Walther C.: Das Viskositäts-Temperatur-Diagramm. Petroleum 1930 B. 26 S. 755-757
  39. Piłat S., Piłat E.: Properties of Synthetic Lubricating Oils. Cyclics Hydrocarbons With Twenty-two Carbon Atoms per Molecule. Ind. Eng. Chem. 1941 vol. 33 pp. 1382-1390
  40. Piłat S.: Zarys technologii nafty. Lwów: wyd. Bratniej Pomocy 1939
  41. Wachal A.: Materiały pędne i oleje silnikowe. Warszawa: Wyd. MON 1959
  42. Mc Kenzie K.: Polymer Configuration and Shear Stability. Materiały I Europ. Kongresu Trybologicznego. Londyn 1973 pp. 287-295
  43. Wood L. G.: The Change of Viscosity of Oils Containing High Polymers when Subjected to High Rates of Shear. Brit. J. Appl. Phys. 1950 pp. 202-206
  44. Thomas J. R.: Sonic Degradation of High Polymers in Salutions Journ. Polymer Sci. 1959 vol. 63 pp. 1725-1729
  45. Crail I. R., Neville A. L.: The Mechanical Shear Stability of Polymeric VI. Improvers. J. Inst. Petr. 1969 vol. 55 pp. 100-108
  46. Gisser H., Petronio M.: Friction of Polymer Solution. ASLE Transact. 1967 vol. 10 pp. 58-66
  47. Семенидо Е. Г., Щеголев Н. В.: Вязкостные присадки. В збёре: Моторные и реактывне масла и жидкости. Москва: Изд. Химия 1963
  48. Bartz W. S.: Zagadnienie stabilności i odporności na ścinanie nowoczesnych wielosezonowych olejów silnikowych. Technika Smarownicza 1973 t. 4 s. 140-146
  49. Wilkinson W. L.: Ciecze nienewtonowskie. Warszawa: WNT 1963
  50. Freund M., Mozes G., Fenyi M.: Rheologische Eigenschaften der mit Polymer-Zusatz legierten Motoren-Schmieröle. Schmiertechnik 1963 B. 10 S. 136-142, 208-214, 345-350, 1964 B. 11 S. 95-99, 151-156, 217-219, 356-361
  51. Wiślicki B.: Metody oceny odporności olejów smarowych i cieczy hydraulicznych na działanie mechanicznych sił ścinających. Referat wygłoszony w NOT 14.05.1968
  52. Wiślicki B., Karpiński W.: Ultraschallmethode als Auswertung der Widerstandfähigkeit der Schmier und Hydrauliköle gegen mechanische Scherkrafte. Referat na 9 Sympozjum „Schmierstoffe” Lipsk sierpień 1967
  53. Heymach H. J., Jost D. E.: Alteration of Molecular Weight Distribution of Polymers by Ultrasonic Energy. Journ. Polymer Sci. 1969 vol. 25 pp. 145-153
  54. Butyagin P. J.: Nature of Mechanical Degradation of Polymethacrylate. Journ. Polym. Sci. 1967 vol. 34 No. l pp. 28-35
  55. Porter R. S., Cantow M. J., Jolmson J. F.: Sonic Degradation of Polyisobutene in Solution Journ. Appl. Phys. 1964 vol. 35 pp. 15-18
  56. Pinkus O., Sterniicht B.: Theory of Hydrodynamic Lubrication. New York: Mc Graw Hill 1961
  57. Колмогоров В. Л., Орлов С. И., Колмогоров Т. Л.: Гидродинамическая подача смазки. Москва: Металургйя 1975
  58. Розенберг И. А.: Влияние смазочных масел на надёжность и долговечность машин. Москва: Машиностроение 1970
  59. Петрусевич А. И.: Основные выводы из контактногидродинамйческой теории смазки. Изд. АН СССР ОТН 1951 № 2 с. 32-38
  60. Peppler W.: Die Theorie der hydrodynamischen Schmierung. VDI Berichte 1957 B. 20 S. 150-158
  61. Reynolds O.: On the theory of lubrication and its application to Mr Beauchamp Tower's experiments. Phil. Trans. Roy. Soc. 1886 vol. 177 part l pp. 153-368
  62. Sterniicht B.: Energy and Reynolds Considerations in Trust-bearing Analysis. Proc. of Conf. on Lubr. and Wear IME 1957
  63. Cameron A., Wood L.: The Full Journal Bearing Proc. Inst. Mech. Eng. 1940 vol. 161 pp. 559-565
  64. Milne-Thomson L. M.: Theoretical Hydrodynamics London: MacMillan 1949
  65. Morgan T. V., Cameron A.: Mechanism of Lubrication in Porous Metal Bearings. Conf. on Lubrication and Wear. Paper 89. London 1957
  66. Sternlicht B., Maginnis F. J.: Application of Digital Computers to Bearings Design. Trans. ASME 1957 No 10 pp. 359-364
  67. Dowson D., Higginson G. R.: Elastohydrodynamic Lubrication. London: Pergamon Press 1966
  68. Shell Intern. Co: The Lubrication of Industrial Gears. London: Shell 1964
  69. Ynh-Hwang Tsao, Kin N. Zang.: A Model for Mixed Lubrication. ASLE Transactions 1975 vol. 18, No. 2 pp. 52-58

    

Last modified:
29-07-2012: Dzięki za uwagi M.D.

All rights reserved
© Wszystkie prawa zastrzeżone