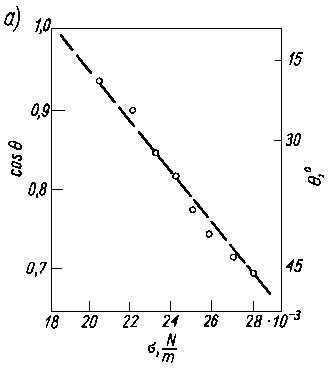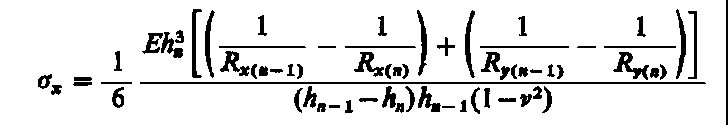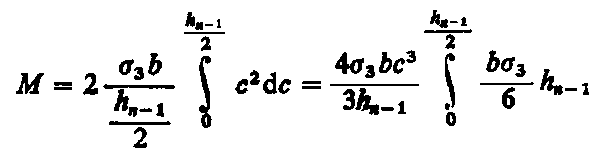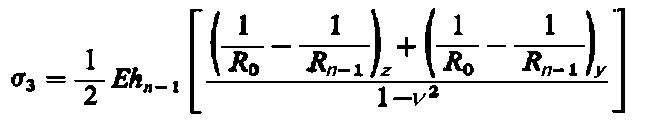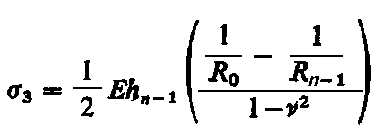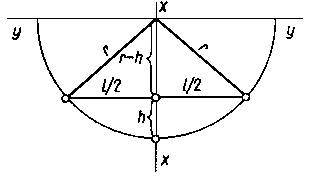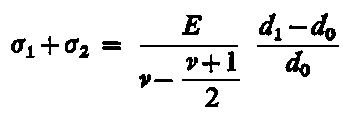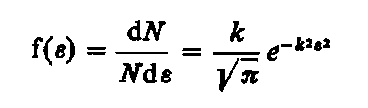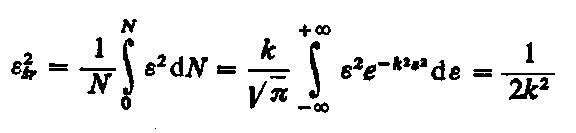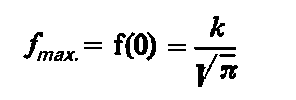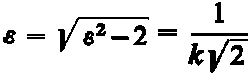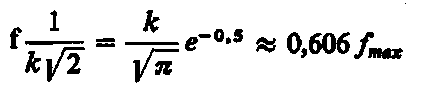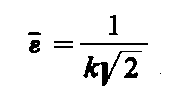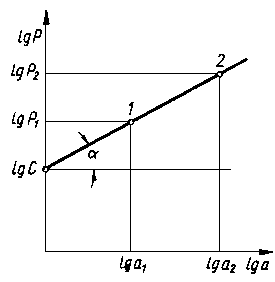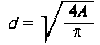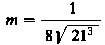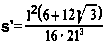| |
Wartości hp (3.19) i rzeczywistej powierzchni styku wyznacza się z profilogramów dla określonego zbliżenia a lub też modelują tę wartość, np. grubością luminoforu.
Podczas pomiarów pod obciążeniem nierówności badanej powierzchni są odkształcone sprężyście i plastycznie. W wyniku tego następuje zmiana ich kształtu. Dlatego też wartości hp i rzeczywista powierzchnia styku zależą poza mikrostrukturą powierzchni od obciążenia i własności mechanicznych badanej warstwy wierzchniej i elementu kontrolnego. Na obecnym etapie badań najczęściej jest stosowana metoda Mechau, w której wykorzystano efekt zakłócenia całkowitego wewnętrznego odbicia światła w punktach styku pryzmatu pomiarowego z wierzchołkami nierówności powierzchni. Metoda ta pozwała na wizualną ocenę liczby, wielkości i rozmieszczenia obszarów styku. Zastosowanie układów fotometrycznych pozwala na prowadzenie pomiarów ilościowych hp i rzeczywistej powierzchni styku.
W znacznie węższym zakresie są stosowane pozostałe metody (np. graficzne, elektryczne, luminescencyjne). Produkowane obecnie niektóre profilometry umożliwiają pomiar hL (3.18) dla zbliżenia względnego e = 0,1. Rzeczywistą powierzchnię styku dla danych powierzchni można obliczyć zakładając, że jest ona funkcją zbliżenia a i siły normalnej dociskanych elementów maszyn
Analityczne obliczenie zbliżenia a lub rzeczywistej powierzchni styku wymaga ustalenia warunków badań i przyjęcia modelu nierówności. Zakłada się, że styk jest plastyczny, jeżeli co najmniej jedna ze stykających się nierówności została odkształcona plastycznie. Styk sprężysty występuje wówczas, gdy w wyniku nacisku następuje tylko sprężyste odkształcenie nierówności. Dla odkształcenia plastycznego rzeczywista powierzchnia styku może być wyrażona zależnością
gdzie: N - obciążenie normalne w N, c - współczynnik uwzględniający różnicę warunków, w których następuje odkształcenie powierzchniowe materiału przy próbie twardości i podczas tarcia, H - twardość wg Brinella w Pa.
Przy odkształceniu sprężystym w obszarach tarcia dla obliczenia rzeczywistej powierzchni styku można korzystać z wzoru Hertza określającego zależności występujące przy kontakcie kuli z płaszczyzną
|
Sn = |
N 2 / 3 r 2 / 3 |
[ |
3 Ek + 4 Gk
Gk(3 Ek + Gk) |
+ |
3 Ep + 4 Gp
Gp(2 Ep + Gp) |
] |
m²
| (3.41)
|
gdzie: N - obciążenie normalne w N, r - promień kuli w m, E, G - współczynnik sprężystości wzdłużnej i poprzecznej w Pa, k, p - indeksy odnoszące się odpowiednio do kuli i płaszczyzny.
W rzeczywistych warunkach tarcia zachodzi jednocześnie odkształcenie plastyczne i sprężyste powierzchni tarcia. Z tego powodu nie można wg podanych wyżej wzorów dokładnie obliczać wartości rzeczywistej powierzchni styku. Najdokładniej można wyznaczyć rzeczywistą powierzchnię styku przez zastosowanie odpowiedniego modelu. Budowa modelu pręcikowego polega na tym, że stan nierówności powierzchni, uzyskany na podstawie profilografowania, jest ukształtowany za pomocą pręcików (rys. 3.16) o wysokości h odpowiadającej wysokości nierówności w badanym obszarze AB.
W analizie procesów tarcia, opartej na modelu pręcików, wartość współczynnika tarcia jest zależna od obciążenia i chropowatości powierzchni trących.
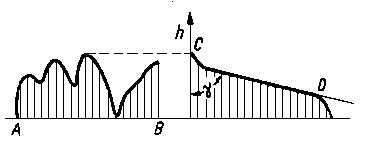 |
Rys. 3.16. Pręcikowy model stanu nierówności powierzchni
|
Po dociśnięciu chropowatej powierzchni do powierzchni nieodkształcalnej i idealnie gładkiej CD (rys. 3.16) pole zakreskowane jest równoważne objętości nierówności odkształconego metalu przy zbliżeniu płaszczyzn o określoną wartość.
Niezależnie od badań stanu nierówności powierzchni ciał stalach rozpatruje się również stan ich powierzchni. Obserwacje makronierówności powierzchni prowadzi się gołym okiem, obserwacje mikronierówności wykonuje się za pomocą mikroskopu optycznego i elektronowego, a obserwacje powierzchni w skali submikroskopowej za pomocą mikroskopów polowych jonowego i elektronowego.
Zasadniczym elementem polowego mikroskopu jonowego jest komora szklana zaopatrzona w fluoryzujący ekran. Naprzeciw ekranu jest umieszczona bardzo cienka i ostra monokrystaliczna igła badanego metalu chłodzona ciekłym wodorem. W komorze znajduje się rozrzedzony hel lub neon (rys. 3.17). Do ostrza ekranu
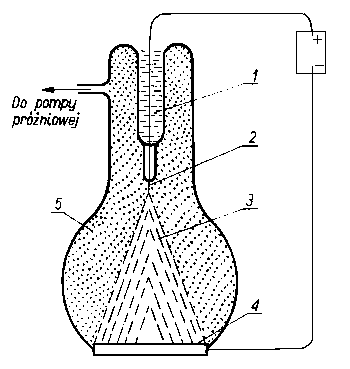 |
Rys. 3.17. Model działania jonowego mikroskopu polowego ;
- ciekły wodór,
- ostrze metalowe,
- jony helu,
- ekran fluoryzujący,
- atomy helu
|
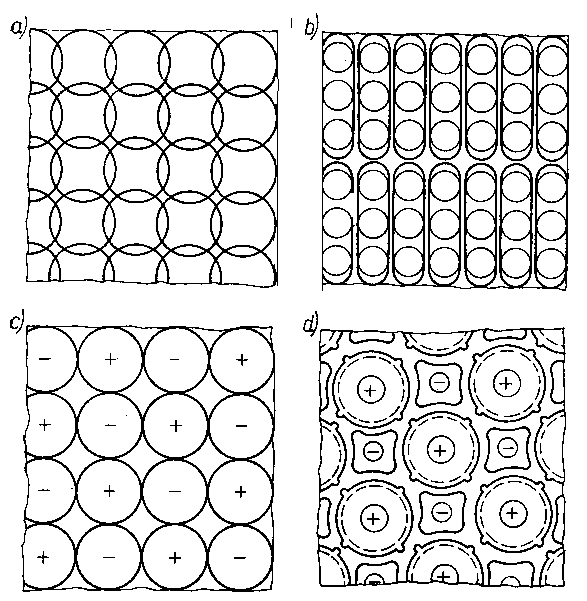
przykłada się napięcie elektryczne, powodujące powstanie na ostrzu wysokonapięciowego pola elektrycznego rzędu kilkuset milionów V/cm. Jeżeli obojętny atom helu znajdzie się dokładnie ponad jakimś atomem ostrza, wówczas zostaje zjonizowany i jako dodatni jon (po oderwaniu elektronu) zostaje przyspieszony w kierunku punktu na ekranie odpowiadającym położeniu atomu, nad którym nastąpiła jonizacja. W ten sposób na ekranie uzyskuje się obraz o doskonałej rozdzielczości.
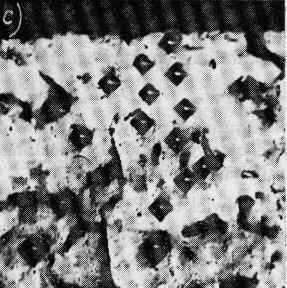
Na rys. 3.18 przedstawiono obraz uzyskany za pomocą polowego mikroskopu jonowego dla ostrza platynowo-irydowego. Przy takim wielkim powiększeniu ostre ostrze okazało się półkulą, która przecina płaszczyzny metalograficzne metalu, tworząc układ okrągłych krystalicznych ścianek.
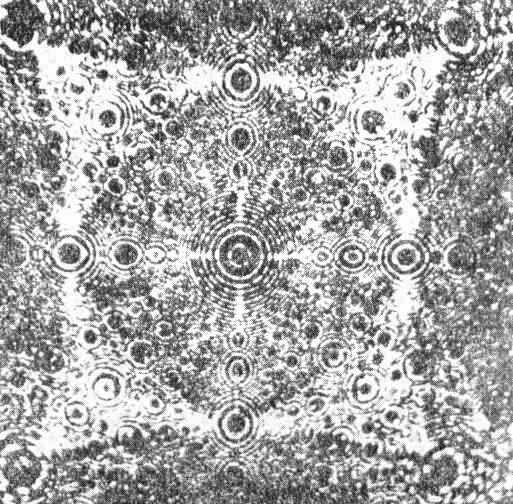 |
Rys. 3.18. Obraz powierzchni stopu platynowo-irydowego uzyskany za pomocą polowego mikroskopu jonowego
|
Za pomocą polowego mikroskopu jonowego można oczyścić powierzchnie badanego ostrza, gdyż pole elektryczne rzędu pół miliarda V/cm powoduje usunięcie z powierzchni nawet najsilniej z nią związanych zanieczyszczeń.
Pola elektryczne o tak dużym natężeniu, jakie panuje w jonowym mikroskopie polowym, wytrzymują tylko najbardziej trwałe metale. Inne ulegają w tych warunkach zupełnemu zniszczeniu. Znacznie niższe natężenie pola elektrycznego występuje w polowym mikroskopie elektronowym (rzędu 20-80 min V/cm), którego zasada działania jest podobna do zasady działania mikroskopu jonowego, tylko że zamiast jonów do tworzenia obrazu wykorzystuje się elektrony. Ze względu na to, że ruch elektronów nie jest prostoliniowy, dyspersja i dyfrakcja elektronów pogarszają w znacznym stopniu rozdzielczość obrazu.
Obydwa te rodzaje mikroskopów polowych są bardzo przydatne do badania struktury powierzchni metali.
3.5.2. Metody badania stanu energetycznego powierzchni
3.5.2.1. Podział metod badania stanu energetycznego powierzchni
Metody wyznaczania energii powierzchni ciał stałych można podzielić na dwie grupy: obliczeniowe i eksperymentalne.
Metody obliczeniowe
mogą być stosowane wtedy, gdy są znane parametry sieci kryształu. Zapewniają one uzyskanie względnie dobrych wyników w przypadku pojedynczych kryształów o modelowej budowie siatki przestrzennej. Przy tych metodach nie można uwzględnić różnych rodzajów defektów sieci krystalicznej, które mają zasadniczy wpływ na wartość energii powierzchni. Dlatego też metody te nie mogą być stosowane do obliczania energii powierzchni metali, ponieważ nie ma ogólnie przyjętej teorii sieci krystalicznej. W przypadku kryształów jonowych, nawet dla najlepiej poznanych kryształów-halogenków metali alkalicznych-otrzymuje się przy wyjściu z różnych założeń różne wartości energii powierzchni.
Metody obliczeniowe nie nadają się również do określenia energii i potencjału powierzchni technicznych, ponieważ nie potrafimy ustalić w jakim stanie znajdują się kryształy powierzchniowe po obróbce mechanicznej i jak zostały zdeformowane sieci krystaliczne. Zastosowanie rachunku prawdopodobieństwa do obliczenia rozkładu defektów sieciowych na powierzchni umożliwia tylko przybliżone oszacowanie wartości energii i potencjału powierzchni.
Nie ma także uniwersalnej metody eksperymentalnej,
za pomocą której można by uzyskać pewne i dokładne wyniki pomiaru energii powierzchniowej. Większość proponowanych metod odnosi się do kryształów kruchych, głównie różnego rodzaju soli. W metodach tych mierzy się ilość energii potrzebnej do zwiększania powierzchni kryształów przez ich rozłupywanie, zarysowywanie, mielenie, wiercenie, szlifowanie. Efektywność metod zależy od możliwości rozróżniania energii włożonej w rozdrabnianie kryształu, czyli zużytej na zwiększenie powierzchni i energii odkształcenia sprężystego, odkształcenia plastycznego oraz energii cieplnej i dźwiękowej.
Jedną z proponowanych metod jest metoda zanikających ruchów wahadła. Metoda ta polega na zastosowaniu wahadła zakończonego twardym ostrzem (diament lub hartowana stal). Wahadło to wyprowadzone ze stanu równowagi wykonuje ruchy zanikające. Jeśli ostrze nie wchodzi w ciało i nie niszczy struktury krystalicznej, to zanik ruchów wahadła następuje głównie wskutek oporu powietrza. W takim przypadku zanikanie ruchu wahadła jest bardzo powolne. Jeśli ostrze rysuje ściankę kryształu, to tym łatwiej będzie ono wchodzić w kryształ im mniejsza jest energia powierzchniowa kryształu. Jeśli kryształ jest kruchy, to ostrze powoduje rozdrobnienie, powstaje proszek, którego energia powierzchniowa jest większa niż energia powierzchniowa kryształu. Jeżeli ciało jest plastyczne, to ostrze wgniata ciało powodując deformację plastyczną będącą przyczyną zaniku ruchu wahadła. Czas potrzebny do zaniku ruchu wahadła lub liczba wahań zależy od energii powierzchniowej, granicy płynności oraz oporu deformacji plastycznych ciał plastycznych. Im mniejsza jest energia powierzchniowa, tym głębiej wchodzi ostrze i tym krótszy jest czas zaniku ruchu wahadła i mniejsza liczba wahnięć.
Drugą metodą stosowaną do badania kryształów kruchych jest metoda rozłupywania kryształów, np. przez pomiar izochorycznego potencjału powierzchni kryształu Nad. Metoda pomiaru polega na tym, że w poziomo ustawiony nóż przyciśnięty do ścianki umocowanego w kowadełku kryształu uderzało wahadło, którego energię uderzenia można było łatwo obliczyć. Pomiary wykonane przy zastosowaniu tej metody w przypadku kryształu NaCl wykazały, że do ukształtowania ściany lustrzanej (100) potrzebna była energia 30 µJ/cm², a dla ukształtowania powierzchni szorstkiej lub schodkowej potrzebna była energia znacznie większa.
Stosowanych jest wiele modyfikacji tej metody. W metodzie szlifowania mierzy się energię potrzebną do zeszlifowania pewnej ilości ciepła. W obliczeniach zakłada się, że wszystkie utworzone w wyniku szlifowania cząstki mają jednakowe wymiary i jednakowe powierzchnie. Z tak zmierzonych wielkości oblicza się energię powierzchniową.
Metodą szlifowania można określić stosunek energii powierzchniowej różnych płaszczyzn kryształu jonowego. Stosunek energii powierzchniowej Ep płaszczyzn (100), (110) i (111) dla NaCl obliczony teoretycznie, wynosi
|
Ep(110)
Ep(100) |
= 2,50; |
Ep(111)
Ep(100) |
= 5,81 |
| (3.42)
|
Oprócz metody szlifowania zastosowano do wyznaczania energii powierzchniowej również metodę wiercenia pamiętając o tym, że im większą średnicę ma wiercony otwór, tym substancja ma mniejszą energię powierzchniową. Omówione powyżej metody oparte na mechanicznym rozdrabnianiu ciał stałych, mogą mieć zastosowanie jedynie do ciał kruchych. Dla metali, które w normalnych warunkach są ciałami plastycznymi, metody te nie mogą znaleźć zastosowania.
Metodami o bardziej uniwersalnym charakterze są metody kalorymetryczne. W kalorymetrycznych metodach pomiaru ciepła rozpuszczania efekt cieplny jest związany z wielkością powierzchni rozpuszczanego ciała. Im większa jest ta powierzchnia, tym większy efekt cieplny. Jeżeli jest możliwe wyznaczenie powierzchni ciała rozpuszczonego, to po zmierzeniu ciepła rozpuszczania można wyznaczyć energię powierzchniową.
Z energią powierzchniową jest również związane ciepło zwilżania. Mając oznaczoną wielkość powierzchni ciała zwilżanego, można za pomocą odpowiednich obliczeń otrzymać wielkość energii powierzchniowej opierając się na mikrokalorymetrycznym pomiarze ciepła zwilżania. Również na podstawie kąta zwilżania Q, który tworzy kropla nie reagująca z powierzchnią ciała stałego, można wyznaczyć energię powierzchniową. Przy obliczaniu energii powierzchniowej na podstawie kąta zwilżania Q korzysta się ze wzoru na napięcie powierzchniowe ssg między ciałem stałym a gazem
|
ssg = scg |
1 + cos Q
1 - cos Q |
N
m
| (3.43)
|
gdzie scg - napięcie powierzchniowe między cieczą a gazem w N/m.
W metodzie tej przy wyznaczaniu energii powierzchniowej dla metali, próbki metali dokładnie oczyszczone i wypolerowane wygrzewano w piecu rurowym w celu usunięcia zaadsorbowanej warstwy gazów. Dla zapobieżenia utlenianiu nad wygrzewaną próbką przez cały czas pomiaru przepuszczano oczyszczony argon. Kąt zwilżania metali trudno topliwych mierzono zwilżając je kroplą utworzoną z metali łatwotopliwych (ołów, bizmut, i in.) Były również dokonywane próby wyznaczania energii powierzchniowej na podstawie obrazu uzyskiwanego za pomocą mikroskopu polowego oraz energii wyjścia elektronu z powierzchni metalu.
3.5.2.2. Zwilżalność ciał stałych przez ciecz
W wyniku działania sił spójności i napięcia błony powierzchniowej cieczy pozioma powierzchnia cieczy w pobliżu ścianek naczynia ulega zakrzywieniu. Obserwuje się wtedy wklęsły lub wypukły menisk cieczy.
Jeżeli ciecz znajduje się w naczyniu, możemy wtedy wyróżnić powierzchnie rozdziału faz: ciało stałe-gaz, ciecz-gaz i ciało stałe-ciecz. Między tymi fazami występują napięcia powierzchniowe, tj. między ciałem stałym a gazem ssg, między cieczą a gazem scg i między ciałem stałym a cieczą ssc. Początkowy kierunek sił napięcia powierzchniowego działających na cząstkę A przedstawiono na rys. 3.19.
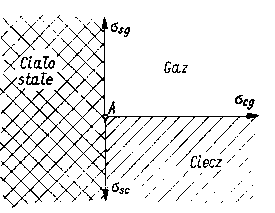
Rys. 3.19. Zachowanie się cieczy w kapilarach |
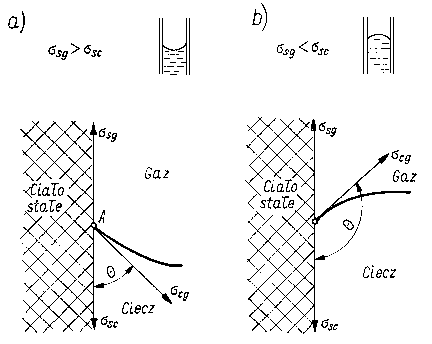
Rys. 3.20. Powierzchnie rozdziału tworzą menisk wklęsły lub wypukły w zależności od różnicy napięć faz badanych ciał:
- ciecz zwilżająca (menisk wklęsły),
- ciecz niezwilżająca (menisk wypukły)
|
Zazwyczaj ssg i ssc sobie równe i wtedy obserwuje się wznoszenie lub opuszczanie cieczy wzdłuż ścianki naczynia w zależności od tego, która z sił napięcia powierzchniowego jest większa. Jeżeli ssg < ssc, to powierzchnia rozdziału tworzy menisk wklęsły (rys. 3.20), a siła napięcia powierzchniowego scg jest styczną do zakrzywionej powierzchni cieczy. Składowa pionowa tej siły wynosi sgc cos Q a położenie równowagi następuje wtedy, gdy zostaje spełniona zależność
|
ssg = ssc + sgc cos Q
| (3.44)
|
Równanie to czasem określa się mianem równania zwilżania.
Jeżeli ssg < ssc to powierzchnia rozdziału też będzie miała menisk wypukły, gdyż ciecz przy ściance opuści się ku dołowi. Warunek równowagi pozostaje taki sam. W obu przypadkach
|
cos Q = |
ssg - ssc
sgc
| (3.45)
|
Jeżeli cos Q < 0 , to ciecz ma menisk wklęsły i ciecz zwilża ściankę naczynia. Jeżeli cos Q > 0, to ciecz ma menisk wypukły i nie zwilża ścianek. Kąt Q nazywa się kątem granicznym lub kątem zwilżania. Jeżeli kąt zwilżania Q = 0, to istnieje pełne zwilżenie; jeżeli kąt Q = 180°, to wtedy występuje absolutna niezwilżalność.
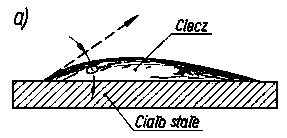
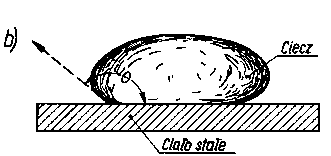
Kąt zwilżania (kąt graniczny) jest to kąt utworzony między zwilżaną powierzchnią ciała stałego a styczną do krzywizny menisku zwilżającej ciec/y, wyprowadzoną z punktu zetknięcia cieczy z powierzchnią ciała stałego (rys. 3.21).
 | 
|
Rys. 3.21. Kąt zwilżania ciała stałego:
- cieczy zwilżającej,
- cieczy niezwilżającej
|
Wartość kąta granicznego dla kropli cieczy umieszczonej na podłożu ciała stałego zależy od równowagi następujących rodzajów sił:
- kohezyjnych sił przyciągania między cząsteczkami cieczy,
- sił przyciągania cząsteczek cieczy przez elementy budowy (jony, cząsteczki, zręby atomowe) powierzchni ciała stałego w miejscach zetknięcia ciecz - ciało stałe,
- sił przyciągania cząsteczek cieczy nie mających kontaktu z powierzchnią ciała stałego, ale znajdujących się w zasięgu oddziaływań międzycząsteczkowych,
- sił grawitacyjnych (sił ciężkości).
Siły kohezyjne zwiększają kąt zwilżania, a pozostałe zmniejszają ten kąt. W przypadku, gdy nie uwzględnia się działania siły ciężkości, wartość kąta zwilżania można obliczyć.
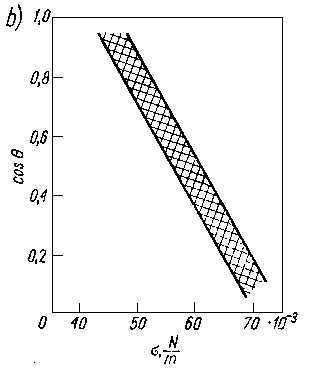
Jak wykazały badania eksperymentalne, między kątem zwilżania a napięciem powierzchniowym istnieje prostoliniowa zależność (rys. 3.22a). W przypadku, gdy zwilża się jedną powierzchnię cieczami należącymi do jednego szeregu homologicznego, zależność ta jest bardzo ścisła, natomiast w przypadku różnych powierzchni i różnych cieczy poszczególne wartości układają się w pasie o określonej szerokości (rys. 3.22b).
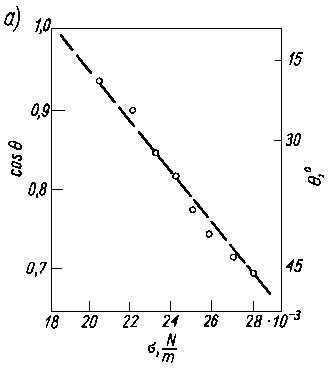 | 
|
Rys. 3.22. Zależność między kątem zwilżania a napięciem powierzchniowym:
- dla powierzchni teflonu i serii n-alkanów,
- orientacyjna dla różnych powierzchni i różnych cieczy
|
Znajomość wartości kąta zwilżania Q ma ogromne znaczenie w procesach flotacyjnych, procesach smarowania, w produkcji tkanin nieprzemakalnych, w produkcji środków pralniczych i detergentów oraz w wielu innych dziedzinach techniki.
3.5.2.3. Praca zwilżania (adhezji)
Ciało stałe i ciecz przed zwilżaniem mają napięcia powierzchniowe ssg i sgc. Z chwilą gdy ciecz zwilża ciało stałe, powstaje wspólna powierzchnia międzyfazowa o napięciu powierzchniowym ssc.
Praca zwilżania przez ciecz ciała stałego Lsc o jednostkowej powierzchni może być wyrażona różnicą napięć powierzchniowych przed zwilżeniem i po zwilżeniu
|
Lsc = ssg + sgc - ssc
| (3.46)
|
Praca zwilżania Lsc jest równa obniżeniu się swobodnej energii powierzchni Es na jednostkę powierzchni w wyniku rozprzestrzeniania warstwy cieczy na powierzchni ciała stałego. W równaniu na pracę zwilżania Lsc występuje napięcie powierzchniowe ciała stałego względem gazu (powietrza), którego nie można wyznaczyć. Należałoby więc zastąpić ssg wielkościami, które można by zmierzyć. Jak widać z rys. 3.23 ciecz
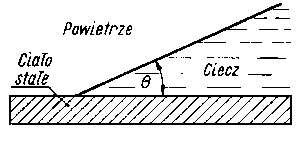 |
Rys. 3.23. Zwilżanie ciała stałego cieczą o dobrych własnościach zwilżających
|
zwilża ciało stałe pod określonym kątem Q. W związku z tym z równania równowagi można obliczyć napięcie powierzchniowe między ciałem stałym a gazem
|
ssg = ssc + scg cos Q
| (3.47)
|
Przez podstawienie do równania (3.46) wartości na ssg otrzymuje się wyrażenie
|
Lsc = ssc + scg cos Q + sgc - ssc
| (3.48)
|
eliminujące nieznaną wartość ssg. Po uproszczeniu otrzymuje się równanie na prace zwilżania ciała stałego o jednostkowej powierzchni, w którym występują jedynie wielkości mierzalne
|
Lsc = scg( 1 + cos Q )
| (3.49)
|
3.5.2.4. Ciepło zwilżania
Ciepło zwilżania jest to ilość ciepła wymieniona z otoczeniem w czasie pracy zwilżania. Eksperymentalnie można go wyznaczyć mierząc kalorymetrycznie ilość ciepła wydzielonego przy zanurzaniu w cieczy litego lub sproszkowanego ciała stałego.
Ze względu na mały efekt cieplny pomiary ciepła zwilżania prowadzi się zazwyczaj stosując sproszkowane ciało stałe, dla którego uprzednio wyznacza się wielkość powierzchni. Do wyznaczania ciepła zwilżania stosuje się kalorymetry zapewniające uzyskanie bardzo dużej dokładności pomiaru.
3.5.2.5. Metoda wyznaczania kąta zwilżania
Kąt zwilżania określa się najczęściej w wyniku pomiaru wymiarów geometrycznych kropli leżącej na powierzchni ciała stałego. Obserwacje prowadzi się za pomocą mikroskopu, w którego okular jest wmontowana podziałka. Lepsze efekty uzyskuje się przez sfotografowanie kropli i powiększenie zdjęcia 80 do 100 x. W tym przypadku wymiary kropli można zmierzyć z dużą dokładnością.
Z wymiarów kropli można łatwo obliczyć kąt zwilżania posługując się zależnością
gdzie: Q - kąt zwilżania, h -wysokość kropli w mm, r - promień kropli w mm, d - kropli w mm.
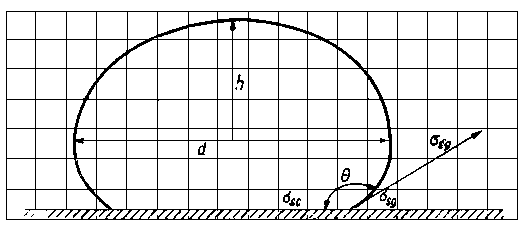 |
Rys. 3.24. Wyznaczanie kąta zwilżania przez pomiar wymiarów kropli
|
Mierząc wymiary geometryczne kropli na powierzchni ciała stałego należy pamiętać o tym, że na wartość kąta granicznego ma zasadniczy wpływ czystość powierzchni metalu oraz temperatura w jakiej przeprowadza się pomiar.
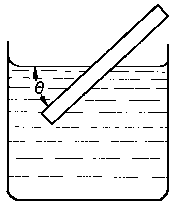 |
Rys. 3.25. Wyznaczanie kąta zwilżania metodą ruchomej płytki
|
Drugą metodą pomiaru kąta zwilżania jest metoda ruchomej płytki. Płytkę wykonuje się z badanej substancji stałej i zanurza w cieczy. Płytkę obraca się dookoła poziomej osi prostopadłej do płaszczyzny rysunku (rys. 3.25) dopóty, dopóki powierzchnia cieczy w punkcie zetknięcia z płytką nie stanie się pozioma. Kąt mierzony wewnątrz cieczy między jej powierzchnią a płytką jest szukanym kątem zwilżania. Powierzchnię linii zetknięcia ogląda się przez mikroskop.
Należy zaznaczyć, że przy wykonywaniu pomiarów mogą wystąpić błędy spowodowane warunkami w jakich wykonuje się pomiar, a zwłaszcza tzw. histerezą kontaktową. Zjawisko to polega na tym, że mierząc kąt zwilżania w kierunku poruszania się kropli oraz w kierunku przeciwnym, otrzymuje się wartości różniące się między sobą znacznie (niejednokrotnie o kilkadziesiąt stopni). Występowanie histerezy kontaktowej przy zwilżaniu tłumaczy się tarciem kropli z podłożem, zjawiskami sorpcyjnymi, nierównościami powierzchni itp.
3.5.3. Metody badania stanu stref podpowierzchniowych
Własności stref podpowierzchniowych warstwy wierzchniej bada się mierząc wartości względne parametrów opisujących jej stan.
3.5.3.1. Metody badania naprężeń własnych w warstwie wierzchniej
W wyniku działania na metal obciążeń zewnętrznych położenie atomów w sieci krystalicznej wykracza poza minimalny poziom energii kinetycznej, zakłócając normalną budowę sieci, a przez to powodując pewien stan naprężeń materiału. Po usunięciu obciążenia tylko część atomów zajmie położenie wyjściowe, a reszta jest przesunięta powodując naprężenie własne materiału.
W zależności od wielkości obszaru, w którym występują naprężenia, rozróżnia się naprężenia własne pierwszego, drugiego i trzeciego rodzaju.
Naprężenia własne pierwszego rodzaju, nazywane także makronaprężeniami, równoważą się w granicach obszarów o wymiarach porównywalnych z wymiarami ciała naprężonego. W warstwach płaskorównoległych naprężenia pierwszego rodzaju są stałe, ale zmieniają się w kierunku prostopadłym do powierzchni (istnieje prawie zawsze gradient naprężeń pierwszego rodzaju w przekroju poprzecznym warstwy wierzchniej).
Naprężenia własne drugiego rodzaju, zwane mikronaprężeniami, zajmują obszary porównywalne z objętością poszczególnych krystalitów lub grup krystalitów. Istnieją one w pasmach poślizgu i wśród bloków struktury mozaikowej.
Naprężenia własne trzeciego rodzaju są zmienne w obszarach submikroskopowych. Równoważą się one w obszarach niewielkich grup atomów leżących na granicach bloków struktury mozaikowej, w płaszczyznach poślizgu itp.
Eksperymentalne badanie naprężeń własnych trwałych i zmieniających się w czasie może być wykonane jedną z metod podanych w tabl. 3.3.
Metody usuwania kolejnych warstw materiału naprężonego są proste w zastosowaniu i łatwe do cechowania ilościowego, np. z wykorzystaniem metod tensometrycznych. Jednakże są one metodami niszczącymi i dlatego nie rokują zbyt dużych perspektyw przy badaniu własności warstwy wierzchniej.
Metody półtrepanacyjne (nawiercenie, lokalne odciążanie) nie nadają się do badania stanów warstwy wierzchniej, ponieważ są niedokładne, a zarazem
Tu ma być tabela 3.3
niszczące. Metody te, a zwłaszcza metody skrawania warstwy naprężonego materiału, wymagają odpowiednio dużej bazy pomiarowej i mogą być wykorzystane jedynie jako metody porównawcze, zwłaszcza przy teoretycznej analizie stanów naprężeń własnych.
Pewne znaczenie w analizie rozkładów naprężeń własnych w warstwie wierzchniej mogą mieć metody badań modelowych, a zwłaszcza metody elastooptyczne.
Metody te mogą służyć do jakościowych badań stanów naprężeń własnych w warstwie wierzchniej.
Osobną grupę metod pomiarów naprężeń własnych stanowią metody wciskania penetratora. Ciekawą, a jednocześnie w skali technicznej nieniszczącą metodą, jest metoda Oppela stosowana do oceny pola naprężeń na podstawie pomiaru odcisków przy wciskaniu penetratora Knoopa. W rezultacie szczegółowej analizy mechanicznych i fizycznych metod eksperymentalnego badania naprężeń własnych wykazano istnienie dużej ilości odmian metod opartych na tej samej zasadzie i tych samych założeniach teoretycznych oraz hipotezach, np. metody usuwania kolejnych warstw materiału. Dlatego wybór metody pomiaru naprężeń własnych zależy między innymi od tego, jaki rodzaj naprężeń należy mierzyć.
Metody mechaniczne (trepanacyjne, półtrepanacyjne, częściowych odciążeń, wciskania penetratora) umożliwiają mierzenie w zasadzie makronaprężeń przez pomiar wartości odkształcenia. Metody mechaniczne są ogólnie biorąc metodami niszczącymi. Często za ich pomocą mierzy się rzeczywiste odkształcenia i na tej podstawie rzeczywisty stan naprężenia materiału. Usunięte częściowo naprężenia zależą często od geometrycznego kształtu mierzonej części próbki.
Ścinając stopniowo naprężoną warstwę materiału można określać w przybliżeniu relaksacyjny stan naprężeń zależnością liniową. W procesie relaksacji naprężeń oddzielanie części próbki (skrawanie warstewek) mierzy się wartość naprężeń własnych zależną od wartości usuniętej reakcji na granicy przecięcia, czyli mierzy się naprężenia pierwszego rodzaju.
Naprężenia pierwszego, drugiego i trzeciego rodzaju można mierzyć z zastosowaniem metod fizycznych. Do znanych metod fizycznych pomiaru naprężeń własnych są zaliczane między innymi metody pomiaru zmian własności magnetycznych, oporu elektrycznego, sily termoelektrycznej oraz tarcia wewnętrznego, jako funkcji stanu naprężenia materiału. Wymienione metody umożliwiają jakościową ocenę stanu naprężeń w materiale oraz są na ogół metodami nieniszczącymi i mogą być stosowane przy małym obszarze pomiarowym.
Do metod fizycznych należą również metody rentgenowskie, umożliwiające pomiar zmiany wartości parametrów sieci krystalograficznej. Z krzywych fotometrycznych lub dyfraktograficznych, przy różnych kątach padania wiązki pierwotnej na badaną próbkę, lub porównawczo dla materiału naprężonego i nie naprężonego, można obliczyć wartość naprężeń pierwszego, drugiego i trzeciego rodzaju.
Pomiar naprężeń metodami rentgenowskimi może być wykonany tylko przy ograniczonej grubości warstwy wierzchniej, ponieważ monochromatyczne promieniowanie stosowane do pomiaru stałej sieciowej nie wnika głębiej niż na kilkadziesiąt mikrometrów w warstwę materiału, a jednocześnie nie płyciej niż na kilka mikrometrów.
Celowe programowanie stanu warstwy wierzchniej elementów maszyn procesami technologicznymi oraz dobranie odpowiednich kształtów i wymiarów tych elementów w aspekcie przyszłych warunków eksploatacji maszyn jest uzależnione od opracowania odpowiednich metod badania własności warstwy wierzchniej.
Oprócz ilościowego zbadania pola i rozkładu naprężeń własnych w warstwie wierzchniej konieczna jest szczegółowa analiza fizycznych zjawisk towarzyszących powstawaniu warstwy wierzchniej. Taka analiza może być podstawą badań nad celowym tworzeniem własności warstwy wierzchniej. Dotychczasowe metody doboru warunków obróbki mechanicznej niewystarczająco uwzględniają trwałość eksploatacyjną maszyn.
Metoda Waissmana-Phillipsa. W metodzie tej wyznacza się naprężenie własne w warstwie wierzchniej z równań równowagi zewnętrznej i warunków na powierzchni ciała stałego przez pomiar wartości odkształceń.
Naprężenia oblicza się z odpowiednich przemieszczeń jako funkcji miejsca, do obliczenia których wykorzystuje się siły fikcyjne, równanie przemieszczeniowe i odpowiednie warunki brzegowe.
Mierzony stan odkształcenia wiąże się z obliczonym stanem naprężenia w warstwie wierzchniej poprzez stałe materiałowe.
Metoda wyznaczania wartości i gradientu naprężeń własnych pierwszego rodzaju w warstwie wierzchniej jest opracowana przy założeniu, że naprężenia te są stałe w płaszczyznach równoległych do powierzchni i zmieniają swoje wartości z głębokością w ściśle określony sposób.
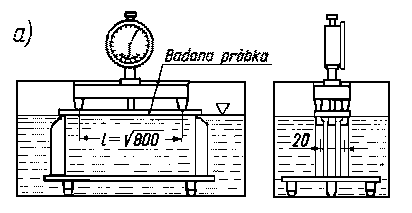
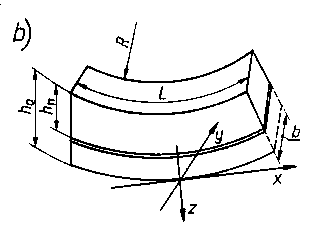
Metoda ścinania warstwy naprężonego materiału przez trawienie jest oparta na modelu mechanicznym. Usuwanie warstwy metalu naprężonego z powierzchni jednej strony płytki wywołuje zachwianie równowagi stanu naprężonego i zmianę wartości krzywizny, aż do ponownego wytworzenia stanu równowagi (rys. 3.26). Przy usuwaniu warstw metalu z tej samej powierzchni w sposób ciągły i rejestrowaniu zmiany krzywizny w zależności od ilości strawionego materiału oblicza się naprężenie własne występujące w każdej usuniętej warstwie.
 |  |
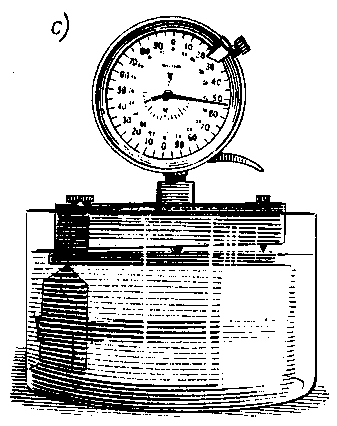 |
Rys. 3.26. Trawienie belki w celu obliczenia naprężeń metodą Waissmanna-Phillipsa
|
Odpowiednie zależności matematyczne wyprowadzono opierając się na schemacie odkształcenia próbki w kształcie belki. Krzywizna ugiętej próbki 1/Rz (w kierunku osi z) obciążonej momentem Mx w płaszczyźnie xz oraz momentem My w płaszczyźnie yz zmienia się wg następujących zależności
|
1
Rz |
= |
12
E h3 |
( |
Mx
b |
- n |
My
L |
) |
1
mm
| (3.51)
|
gdzie: h - grubość próbki w mm, n - liczba Poissona, L - długość próbki w mm, b - szerokość próbki w mm.
Jeśli ulega zmianie wartość odkształcenia próbki od Rz(n-1) do Rz(n), to musi następować zmiana wartości momentu obciążającego próbkę, a więc występuje zależność
|
1
Rz(n-1) |
- |
1
Rz(n) |
= |
12
E h3 |
[( |
Mx(n-1)
b |
- |
Mx(n)
b |
) |
- n |
( |
My(n-1)
L |
- |
My(n)
L |
)]
| (3.52)
|
Jeśli n-ta. naprężona warstwa zostanie usunięta i jeśli średnia wartość naprężenia w jej grubości w kierunku z jest sz(n) to zmiana wartości momentu gnącego wywołana usunięciem materiału wynosi
|
Mx(n-1) - Mx(n) = sz(n) ( h(n-1) - h(n) ) |
h(n-1)
2
| (3.53)
|
Podobną zależność można napisać dla kierunku osi y. Łącząc powyższe równania (3.52) i (3.53), otrzymuje się zależność
|
1
Rx(n-1) |
- |
1
Rx(n) |
= |
6
E h3 |
( h(n-1) - h(n) ) h(n-1) ( sx(n) - sy(n) )
| (3.54)
|
Podobną zależność otrzymuje się przy zmianie krzywizny w kierunku osi y
|
1
Ry(n-1) |
- |
1
Ry(n) |
= |
6
E h3 |
( h(n-1) - h(n) ) h(n-1) ( sy(n) - n sx(n) )
| (3.55)
|
Po rozwiązaniu równań i pomnożeniu ich przez liczbę Poissona i dodaniu równań stronami uzyskuje się średnią wartość naprężenia w kierunku osi z
|
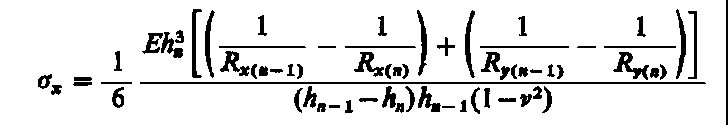
| (3.56)
|
Dla małych krzywizn, przy stosunku wartości promienia ugięcia belki do jej grubości większym od 10 i małych grubościach usuwanych warstw w porównaniu z pozostałą grubością próbki oraz przy założeniu jednokierunkowego działania naprężeń, równanie (3.56) przyjmie postać
|
s1 |
= |
1
6 |
E h2 |
d c
d h
| (3.57)
|
gdzie d c/d h - nachylenie krzywej przedstawiającej funkcję krzywizny względem grubości próbki.
Jeśli naprężenia działają równomiernie we wszystkich kierunkach i są równoległe do powierzchni płaskiej, jak w przypadku powierzchni kuli (Rz - Ry) to w każdej usuwanej warstwie można s1 obliczyć z zależności
|
s1 |
= |
1
6 |
E h2n
1 - n |
d c
d h
| (3.58)
|
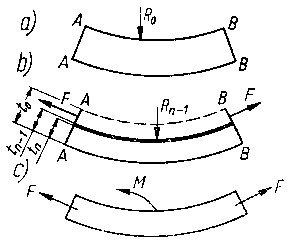 |
Rys. 3.27. Zmiana początkowego promienia krzywizny w zależności od grubości strawionej warstwy i zastąpienie strawionej warstewki fikcyjnej siłami i momentem przy obliczaniu napięć własnych w warstwie wierzchniej
|
W pierwszej usuwanej warstwie s1 jest średnią wartością naprężenia. W każdej następnej usuwanej warstwie wartość naprężenia jest wypadkową średniej wartości naprężenia oraz naprężenia spowodowanego usuwaniem poprzedniej warstwy. Po usunięciu pierwszej warstwy naprężenia w pozostałych warstwach ulegają zmianie. Po usunięciu n - 1 warstw (rys. 3.27) początkowy promień krzywizny Ro przyjmie wartość Rn-1 wskutek usunięcia materiału naprężonego.
Dwie hipotetyczne siły F i moment M rekompensują reakcję usuniętych n - 1 warstw materiału. Działanie sił F i momentu M można obliczyć wprowadzając zmianę naprężenia s2 w n-tej warstwie pod działaniem osiowym wszystkich poprzednich zabiegów usuwania materiału oraz naprężenia s3 w n-tej warstwie pod działaniem momentu rekompensującego wszystkie reakcje poprzednich zabiegów usuwania materiału.
Wartość siły F równoważy naprężenie własne warstw usuniętych
|
n-1 | |
F = - |
S |
s2 b D h
| (3.59) | |
0
|
gdzie s2 b Dh - iloczyn naprężenia przez przekrój poprzeczny usuniętej warstwy.
Usunięcie działania siły F spowoduje zanik jednorodny naprężeń s2wzdłuż całej nienaruszonej grubości próbki
|
n-2 | |
s2 = |
F '
b hn-1 |
= |
S |
s c D h
hn-1
| (3.60) | |
0
|
Wartość momentu można obliczyć przy założeniu, że zmiany krzywizny próbki są spowodowane tylko zmianami wartości momentu. Usunięcie działania momentu spowoduje zmianę krzywizny na grubości hn-1 od R0 do Rn-1 czyli występuje zależność
|
1
R0 |
- |
1
Rn-1 |
= |
12
E h3n-1 |
( |
M0 - Mn-1
b |
- n |
M0 - Mn-1
L |
)
| (3.61)
|
Jeśli moment działający zmieni rozkład naprężeń w przekroju poprzecznym liniowo (płaszczyzny poprzeczne są płaskie podczas zginania), to zmiana wartości momentu wynikająca z poprzednich zabiegów usuwania warstw jest podana zależnością
|
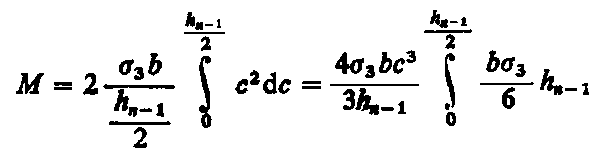
| (3.62)
|
Łącząc oba równania (3.61) i (3.62), otrzymamy
|
1
R0 |
- |
1
Rn-1 |
≈ |
12
E h3n-1 |
( |
1
6 |
s3 h2n-1 |
- |
n
6 |
s3 h2n-1 |
)
| (3.63)
|
|
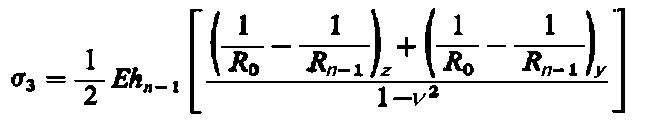
| (3.64)
|
Przy dwuosiowym (płaskim) stanie naprężeń
|
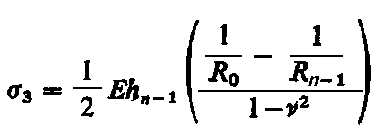
| (3.65)
|
W przypadku ogólnego stanu naprężeń, przy 1/R = c, wypadkowe naprężenie
|
s1 = |
1
6 |
E h3n
|
[ |
( cn-1 -cn )z + ( cn-1 - cn )y
( hn-1 - hn ) hn-1 ( 1 - n2 ) |
]
| (3.67)
|
|
n-1
| |
s2 = - |
S |
sx D h
hn-1
| (3.68)
| |
0
|
|
s1 = |
1
2 |
E hn-1
|
[ |
( c0 -cn-1 )z - ( c0 - cn-1 )y
1 - n2 |
]
| (3.69)
|
W przypadku dwuosiowego stanu naprężeń i cienkich warstw usuwanego materiału
|
s1 = |
1
2 |
E |
h2n
1 - n2 |
d c
d h
| (3.71)
|
|
n-1
| |
s2 = - |
S |
sx D h
hn-1
| (3.72)
| |
0
|
|
s1 = |
1
2 |
E hn-1
|
c0 -cn-1
1 - n2
| (3.73)
|
W przypadku jednoosiowego stanu naprężeń
|
s1 = |
1
2 |
E h2n |
d c
d h
| (3.75)
|
|
n-1
| |
s2 = - |
S |
sx D h
hn-1
| (3.76)
| |
0
|
|
s1 = |
1
2 |
E hn-1 ( c0 - cn-1 )
| (3.77)
|
Praktycznie warstwę naprężoną usuwa się strawiając ją chemicznie lub elektrochemicznie i mierząc krzywiznę uginającej się belki.
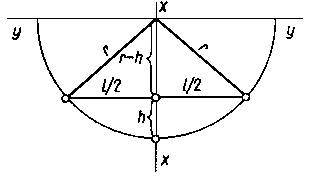 |
Rys. 3.28. Zależności geometryczne niezbędne do obliczania krzywizny C uginającej się belki podczas jej trawienia
|
Nietrawione powierzchnie belki należy pokryć lakierem ochronnym. Korzystnie jest ze względu na łatwość obliczania krzywizny przyjąć długość pomiarową próbki równą L² = 8000 mm.
Wartość krzywizny oblicza się z zależności geometrycznych podanych na rys. 3.28, zakładając kołowe odkształcenie próbki
|
c = |
1
r |
= |
8 h
8000 |
= |
h • 10 -3 mm
| (3.78)
|
Z uzyskanych wyników pomiarów oblicza się gradient, rozkład i głębokość zalegania naprężeń własnych pierwszego rodzaju w WW.
Metody rentgenowskie. Rentgenowskie metody badania naprężeń własnych pierwszego rodzaju pozwalają mierzyć statystyczną wartość odkształcenia parametrów sieci krystalograficznej metalu. Należą one do metod nieniszczących i pozwalają mierzyć naprężenia w elementach maszyn o dowolnych kształtach geometrycznych. Rentgenowskie metody, w przeciwieństwie do metod mechanicznych, umożliwiają badanie odkształcenia metalu w małych obszarach, a nawet w oddzielnych krystalitach polikryształu.
Ujemną cechą rentgenowskich metod jest ograniczona głębokość penetracji promieni rentgenowskich w głąb metalu warstwy wierzchniej. Podstawy teoretyczne wyznaczania stanu naprężeń własnych są oparte na pomiarze odkształceń elementarnego sześcianu. Całkowite wydłużenie e krawędzi 1 sześcianu jest sumą wydłużeń
|
e1 = e '1 + e ''1 + e '''1 = |
s1
E |
- n |
( |
s2
E |
+ |
s3
E |
)
| (3.79)
|
Podobne wyrażenia otrzyma się na wartości odkształceń wypadkowych krawędzi w pozostałych dwóch kierunkach
|
e2 |
= |
s2
E |
- n |
( |
s1
E |
+ |
s3
E |
)
| (3.80)
|
|
e3 |
= |
s3
E |
- n |
( |
s2
E |
+ |
s1
E |
)
| (3.81)
|
W przypadku odkształcenia metalu podlegają wydłużeniu lub skróceniu odległości pomiędzy płaszczyznami krystalograficznymi.
Przy dwuosiowym (płaskim) stanie naprężenia odkształcenie w kierunku prostopadłym do płaszczyzny działania naprężeń jest wyrażone zależnością
|
e3 = e1 = |
Dd
d0 |
= |
d1 - d0
d0
| (3.82)
|
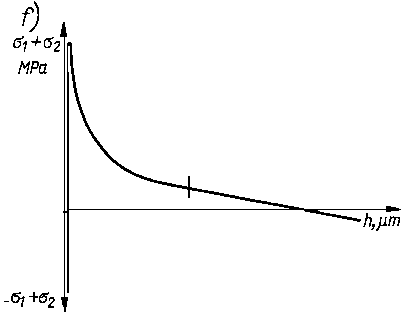
W wyniku pomiaru wydłużenia e prostopadle do powierzchni próbki uzyskuje się sumę naprężeń głównych
|
s1 + s2 = - |
E
n |
d1 - d0
d0
| (3.83)
|
Powyższa zależność określa w przybliżeniu sumę naprężeń głównych, ponieważ w rzeczywistości płaszczyzny krystalograficzne - uginające promienie rentgenowskie przy prostopadłym naświetlaniu próbki - nie są do niej równoległe, lecz nachylone pod kątem Q = 90 - Q, gdzie Q jest kątem odbłysku Bragga.
Systematyczny błąd, który się popełnia przy obliczaniu sumy naprężeń dla promieniowania Fe lub Co wynosi około 6% (otrzymuje się mniejszą wartość naprężeń od rzeczywistych o około 6%).
Według Glockera dokładny wzór na sumę naprężeń głównych ma postać
|
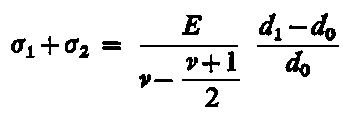
| (3.84)
|
Stan naprężenia w danym punkcie jest określony, jeśli zostaną podane kierunki i wartość naprężeń głównych. Aby to zagadnienie rozwiązać dokładnie, potrzebne są cztery zdjęcia rentgenowskie: jedno prostopadłe i trzy ukośne. Wartości i odległości między płaszczyznami oblicza się z odpowiednich rentgenogramów.
Rentgenogramy można sporządzić w płaskiej kamerze wstecznej, w płasko-stożkowej kamerze wstecznej, w kamerze Debye'a-Scherrera, w kamerze ogniskującej i innych lub dyfraktogramy sporządzone w dyfraktografach.
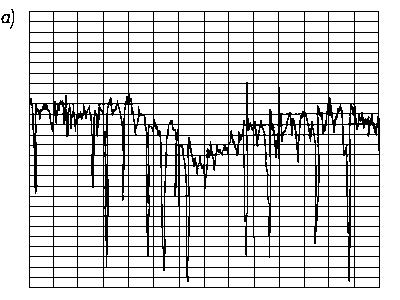
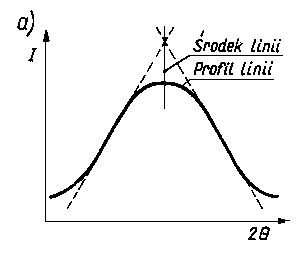
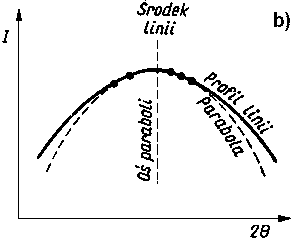
Dokładność pomiaru naprężeń własnych jest zależna od dokładności pomiaru środka linii dyfrakcyjnej. W przypadku jednorodnych makronaprężeń i mikronaprężeń w warstwie wierzchniej próbek uzyskuje się linie dyfrakcyjne zarówno przesunięte, jak i rozmyte (rozszerzone). Przesunięcie linii dyfrakcyjnych mierzy się przy badaniach dyfraktometrycznych na wyznaczonym profilu linii z zapisu mikrofotometrycznego błony filmowej lub z bezpośredniego pomiaru natężenia wiązki ugiętej przy różnych wartościach kątów Q. Położenie środka linii (wierzchołka krzywej) wyznacza się ekstrapolując odcinki proste krzywej mikrofotometrycznej aż do punktu przecięcia prostych. Punkt ten przyjmuje się jako środek linii fotometrycznej. W niektórych przypadkach, gdy linia mikrofotometryczna jest niesymetryczna i o szerokim profilu, a w wierzchołku ma kształt paraboli, wtedy maksymalną wartość natężenia linii określa się metodą dopasowania paraboli. Wartość 2 Q wyznacza się za pomocą tej metody z dokładnością 0,02°. Metoda ekstrapolacji prostych odcinków profilu linii i metoda dopasowania paraboli są podane na rys. 3.29.
 | 
|
Rys. 3.29. Metody:
- ekstrapolacji odcinków profilu krzywej fotometrycznej,
- dopasowania paraboli do wierzchołka krzywej fotometrycznej,
I - natężenie promieniowania
|
Dokładność pomiaru parametru sieci, a więc i naprężeń własnych, jest zależna od dokładności odczytu kąta dyfrakcji. Dokładność pomiaru wartości d lub a zależy więc od dokładności pomiaru wartości funkcji sinQ. Dokładną wartość sinQ można otrzymać z pomiaru kąta Q pod warunkiem, że wartość ta jest zbliżona do 90° (rys. 3.29). Potwierdza to również zróżniczkowane równanie Bragga określające przyrost parametru sieci do jego całkowitej wartości
|
D d
d |
= |
ctg Q • D Q
| (3.85)
|
Błąd względny spowodowany błędem pomiaru kąta Q dąży do zera, jeśli kąt Q dąży do 90° (rys. 3.30).
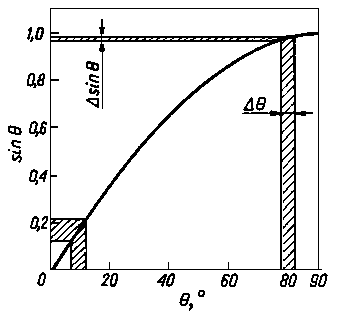 |
Rys. 3.30. Metody: Zależność funkcji sinQ od kąta Q
|
Przy dokładnym wyznaczeniu odległości między płaszczyznami krystalograficznymi należy uwzględniać takie błędy, jak kurczenie się błony fotograficznej, błąd promienia kamery, niecentryczność próbki, absorpcję promieni rentgenowskich w materiale próbki oraz błąd pomiaru odległości między preparatem a błoną filmową. Ważnym czynnikiem przy badaniu naprężeń własnych w warstwie wierzchniej jest ocena głębokości wnikania promieni rentgenowskich w głąb materiału próbki. Płaska powierzchnia próbki oraz monochromatyczne promienie rentgenowskie, padające na tę powierzchnię pod kątem a, o natężeniu Io, są po ugięciu rejestrowane pod kątem b.
Wiązka padająca ulega absorpcji w preparacie. Głębokość wnikania promieni rentgenowskich określa rodzaj materiału naświetlanego i rodzaj promieniowania. Natężenie wiązki pierwotnej maleje wykładniczo ze wzrostem grubości badanej warstwy metalu.
Przy badaniach gradientu naprężeń własnych w warstwie wierzchniej można regulować głębokość wnikania promieni przez zmianę kąta a oraz zmianę długości fal promieniowania rentgenowskiego.
Miarą naprężeń własnych drugiego rodzaju
jest stosunek przyrostu parametru sieci do jego całkowitej wartości Dd/d obliczany z pomiaru krzywych fotometrycznych poszczególnych linii rentgenogramów. Przy obliczaniu naprężeń własnych drugiego rodzaju wykorzystuje się średnią szerokość (połówkową) krzywej fotometrycznej lub dyfraktograficznej. Przyjęcie do obliczeń wartości połówkowych wynika stąd, że krzywe fotometryczne o tej samej wysokości mogą mieć różne szerokości podstawy i wierzchołka. Średnia szerokość krzywej fotometrycznej świadczy o statystycznym odkształceniu parametru sieci w badanym mikroobszarze. Krzywe fotometryczne materiałów nieodkształconych są ostre (nie rozmyte) i mają wyraźne dublety k a1 i k a2.
Przy wprowadzeniu zależności do obliczania naprężeń własnych drugiego rodzaju przyjęto założenie, że rozkład odkształceń w badanym materiale jest zupełnie przypadkowy i odpowiada rozkładowi normalnemu dla błędu przypadkowego.
Liczbę krystalitów N, których odkształcenie jest zawarte pomiędzy e a e + d e można wyrazić wzorem
|
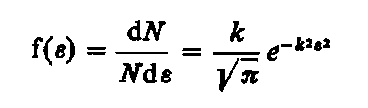
| (3.86)
|
Z tego równania oblicza się wartość kwadratu średniego odkształcenia
|
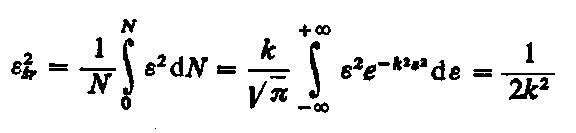
| (3.87)
|
Wykresem funkcji f(e) jest krzywa rozkładu normalnego, której maksimum występuje przy e=0 i wynosi 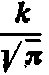
|
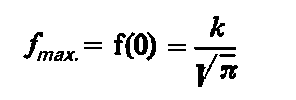
| (3.88)
|
gdzie k - stała.
| W punkcie | 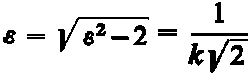 | wartość funkcji f (e) wynosi |
|
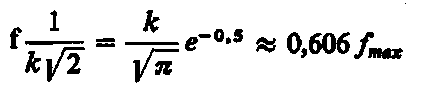
| (3.89)
|
Jeśli krzywą f(e) przetnie się linią równoległą do osi na wysokości 0,606 fmax, to punkty przecięcia wyznaczą wartość
|
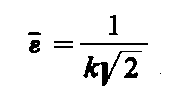
| (3.90)
|
Wartość odkształcenia obliczona z tego równania jest miarą odkształcenia świadczącego o występowaniu naprężenia drugiego rodzaju. Naprężenia te powodują ugięcia promieni rentgenowskich pod kątami różnymi od kąta Bragga o wartość D Q.
Odkształcenie materiału, proporcjonalne do funkcji f(Q), dla kąta Bragga wyrażono zależnością
|
e = |
D d
d |
= |
1
tg Qb |
D Q
| (3.91)
|
Przyjmując, że zaczernienie błony fotograficznej jest proporcjonalne do natężenia promienia padającego, kształt krzywej zaczernienia jest geometrycznie podobny do krzywej f(Q). Oznacza to, że ze wzrostem naprężeń drugiego rodzaju wartości stałej k maleją. Świadczy to więc o tym, że wysokość krzywej fotometrycznej maleje, a jej szerokość rośnie.
Pomiaru szerokości krzywej fotometrycznej dokonuje się zazwyczaj nie na wysokości 0,606 fmax, ale na wysokości 0,5 fmax (szerokość połówkowa).
Oznaczając przyrost kąta ugięcia Q dla szerokości połówkowej przez D Q0,5 i odpowiadające mu odkształcenie przez e0,5 można wartość średniego odkształcenia obliczyć z zależności
|
eśr = |
0,85 e0,5 = |
0,85 Q0,5
tg Qb
| (3.92)
|
W przypadku naprężeń drugiego rodzaju składowe odkształcenia ex, ey, ezsą niezależne i dlatego nie można obliczyć składowych naprężenia. Średnią wartość naprężenia drugiego rodzaju oblicza się z zależności
|
s0 = |
E
1 - 2n |
e0 = |
E
1 - 2n |
0,85 D Q0,5
tg Qb
| (3.93)
|
Średnia wartość naprężenia drugiego rodzaju jest tylko umowną miarą stanu materiału, ponieważ przy wyprowadzaniu tego wzoru posłużono się średnim odkształceniem, wyrażającym tylko zmianę objętości, a nie uwzględniającym zmiany kształtu krystalitów pod wpływem lokalnych naprężeń własnych.
Zmiany intensywności ugięcia wiązki promieni rentgenowskich spowodowane naprężeniami własnymi trzeciego rodzaju są podobne do zmian wywołanych cieplnymi drganiami atomów. Zmniejszenie intensywności ugięcia promieni rentgenowskich jest wynikiem sumarycznego działania statycznych i dynamicznych skażeń sieci.
Spadek intensywności wiązki ugiętej w materiale odkształconym jest określony zależnością
przy czym
|
M = |
8
3 |
π ² U ² |
( |
sin Q
l |
) |
gdzie: Id - intensywność wiązki promieni rentgenowskich ugiętej w materiale odkształconym, I0 - intensywność wiązki promieni rentgenowskich ugiętej w materiale nieodkształconym. U ² - średnia wartość kwadratu wychylenia atomów z położenia równowagi siatki krystalograficznej nieodkształconej, wartość U dla opiłek Cu wynosi 0,0038 nm, a dla opiłek Ni 0,0196 nm, l długość fali promieniowania rentgenowskiego.
Po obustronnym zlogarytmowaniu równania (3.94) i podstawieniu w miejsce sin Q/l wartości U/2d, można na podstawie równania Bragga napisać
|
ln |
Id
I0 |
= - |
4
3 |
π ² U ² |
( |
n
d |
) ²
| (3.95)
|
Dal układu regularnego otrzymuje się
|
U²
a² |
= - |
3
4 π ² |
1
n² ( h² + k² + l² ) |
ln |
I0
Id
| (3.96)
|
Wyrażenie U ²/a ² jest miarą naprężeń trzeciego rodzaju w sieci krystalograficznej układu regularnego, ściślej biorąc podaje skażenie sieci, a nie rzeczywiste naprężenie. Intensywności ugiętych wiązek promieni rentgenowskich są podane w skali bezwzględnej. Bezwzględna wartość ugiętej wiązki zależy od intensywności wzbudzonego promieniowania, zdolności rozpraszania promieni przez atom, komórkę i kryształ. W badaniach wykorzystuje się względną intensywność wiązki zgiętej.
Wartość naprężeń trzeciego rodzaju można obliczyć z zależności
|
U²
a² |
= |
3
4 π |
1
( H2 - H1 ) |
ln |
I1d/I2d
I1o/I2o
| (3.97)
|
przy czym
|
H1 = h1² + k1² + l1² |
H2 = h2² + k2² + l2²
| (3.98)
|
gdzie: I1o/I2o - stosunek względnych intensywności ugięcia wiązki na płaszczyznach krystalograficznych; o wskaźnikach h1, k1, l1, h2, k2, l2 otrzymany na jednym rentgenogramie z materiału wyżarzonego: I1d/I2d - stosunek względnych intensywności ugięcia wiązki na płaszczyznach krystalograficznych, o wskaźnikach h1, k1, l1, h2, k2, l2 otrzymano na jednym rentgenogramie z materiału naprężonego.
Jak wynika z przytoczonego materiału wszystkie trzy rodzaje naprężeń własnych w warstwie wierzchniej można obliczyć z krzywych fotometrycznych lub krzywych dyfraktometrycznych sporządzonych dla materiału wyżarzonego i naprężonego. Oblicza się zatem względne wartości poszczególnych rodzajów naprężeń.
Gradient naprężeń własnych w warstwie wierzchniej oblicza się metodą trawienia kolejnych warstw materiału naprężonego albo też metodą zmiennej wartości czynnika absorpcji masowej lub czynnika geometrycznego. Stosuje się różne rodzaje promieniowania (różne długości fal promieniowania rentgenowskiego) i różne kąty padania wiązki pierwotnej na badaną powierzchnię. Głębokość zalegania naprężeń można ocenić metodami rentgenowskimi tylko poprzez kolejne usuwanie warstw, np. trawienia materiału naprężonego.
Metoda Oppela. Badanie naprężeń własnych metodą Oppela polega na pomiarze różnicy przekątnych odcisków uzyskanych metodą penetracji wgłębnika w warstwę metalu.
Metoda ta umożliwia dokonanie względnej oceny stanu naprężeń materiału wyżarzonego i naprężonego. Przy zastosowaniu tej metody nie można zmierzyć naprężeń powstałych wyłącznie podczas odkształceń sprężystych.
W zakresie prawa Hooke'a istnieje liniowa zależność między stanem odkształcenia metalu a stanem naprężenia. Przy zmianie wartości naprężeń rozciągających wskaźnik twardości zmienia się intensywniej niż przy analogicznych zmianach naprężeń ściskających.
W celu wyznaczenia dwuosiowego (płaskiego) stanu naprężeń w warstwie wierzchniej należy wyznaczyć kierunki naprężeń głównych i ich wartości.
Naprężenia własne w warstwie wierzchniej bada się mierząc geometrię odcisków i siłę oporu wciskania piramidki Knoopa w badaną warstwę wierzchnią.
Dłuższa przekątna odcisków naniesionych w naprężonej warstwie wierzchniej ma inną wartość niż przekątna odcisków naniesionych pod kątem prostym do kierunku naprężeń głównych.
Cechowanie metody Oppela przeprowadza się na próbkach wyżarzonych, o zerowym stanie naprężeń własnych. Próbkę następnie rozciąga się i mierzy wartość odcisków. Z odpowiedniej wartości wydłużenia oblicza się naprężenie. W wyniku tego cechowania uzyskuje się zależność łączącą stan naprężenia ze zmianą twardości badanego materiału.
Zmianę D H twardości H badanego materiału zdefiniowano jako
gdzie Ho - twardość materiału wyżarzonego.
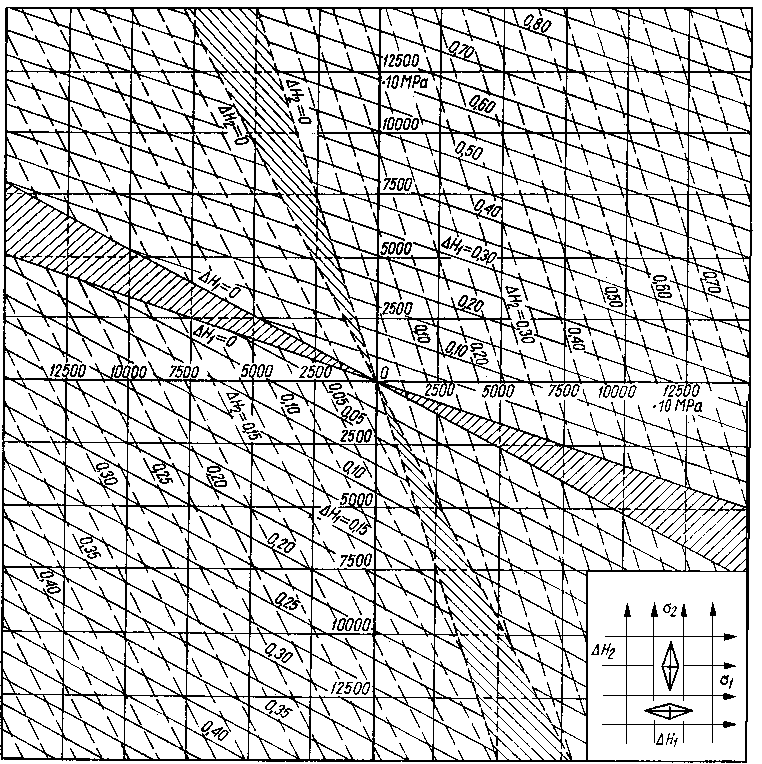 |
Rys. 3.31. Wykres do obliczania naprężeń własnych mierzonych wg metody Oppela
|
Korzystając z wykresu opracowanego dla stali 10 (rys. 3.31) oblicza się wartość przyrostu naprężeń w kierunku równoległym do wzdłużnej osi próbki A.H\, w kierunku prostopadłym do wzdłużnej osi próbki Affz i pod kątem 45°. W zakresie prawa Hooke'a wykres ten może być wykorzystany dla różnych metali.
Liniowa zależność między stanem naprężenia wywołanym obciążeniem zewnętrznym a zmianą twardości materiału jest przedstawiona za pomocą następujących równań
|
sa
E |
= a11 D Ha + a22 D Ha + 90° + a23
| (3.100)
|
|
sa +90°
E |
= a21 D Ha + a22 D Ha + 90° + a23
| (3.101)
|
Wartość współczynników a wyznacza się z pomiarów naprężeń i twardości przy jednoosiowym rozciąganiu. W stanie naprężonym materiału przy D Ha = 0; a13 = a23 = 0. Suma wzajemnie prostopadłych naprężeń normalnych sa i sa +90° jest stała dla wszystkich kierunków w badanym punkcie, zgodnie z kołem naprężeń Mohra
|
sa + sa +90°
E |
= a1 D Ha + a2 D Ha + 90°
| (3.102)
|
Z wyników pomiarów twardości badanych próbek wynika, że
|
D Ha = D Ha + 90°
| (3.103)
|
czyli
|
sa + sa +90°
E |
= ( a1 + a2 ) D Ha
| (3.104)
|
Przy badaniu twardości próbek odkształconych siłami zewnętrznymi uzyskano
|
D Ha = |
1
2 |
( D H1 + D H2 )
| (3.105)
|
Suma naprężeń głównych, przy przyjęciu a = ½ ( a1 + a2 ), jest równa
|
sa + sa +90°
E |
= a ( D H1 + D H2 )
| (3.106)
|
Przyjmując do obliczeń średnią wartość współczynników a, i a^
uzyskuje się
|
sa + sa +90°
E |
= a ( D Ha + D Ha + 90° )
| (3.107)
|
Podobne równanie wyprowadza się dla różnicy prostopadłych do siebie naprężeń głównych
|
sa - sa +90°
E |
= ( a11 - a21 ) D Ha - ( a22 - a12 ) D Ha + 90°
| (3.108)
|
Przyjmując a11 - a21 = b1 oraz a22 - a12 = b2, otrzymano
|
sa - sa +90°
E |
= b1 D Ha - b2 D Ha + 90°
| (3.109)
|
przy czym
|
sa = s1 ;
sa +90° = 0 ;
D Ha = D H1 ;
D Ha + 90° = D H2
| (3.110)
|
Składowe sumy naprężeń głównych obliczono z zależności
|
sa
E |
= |
a
2 |
( D Ha + D Ha + 90° ) |
+ |
b
2 |
( D Ha - D Ha + 90° )
| (3.111)
|
|
sa+90°
E |
= |
a
2 |
( D Ha + D Ha + 90° ) |
- |
b
2 |
( D Ha - D Ha + 90° )
| (3.112)
|
W obszarze zakreskowanym (rys. 3.31) między prostymi ( D H1 = 0 i D H2 = 0) wartości współczynników a i b mają różne wartości.
Z przytoczonych zależności na podstawie prawa Hooke'a oblicza się wydłużenia
|
ea + ea+90° = |
1 - n
E |
( sa + sa+90° )
| (3.113)
|
|
ea - ea+90° = |
1 - n
E |
( sa - sa+90° )
| (3.114)
|
3.5.3.2. Metoda badania umocnienia materiału warstwy wierzchniej
Wskaźnikiem umocnienia materiału jest między innymi wzrost twardości metalu lub gęstości dyslokacji. Przy badaniu stanu umocnienia materiału warstwy wierzchniej nie korzysta się z metod pomiaru gęstości dyslokacji, jeśli są badane materiały o złożonej strukturze. Przy fizykalnej interpretacji zjawiska umocnienia materiału warstwy wierzchniej, zwłaszcza w monokryształach lub strukturach typowo ferrytycznych, pomiar gęstości dyslokacji daje pogląd, jaki jest mechanizm umocnienia. Gęstość dyslokacji można badać przez zliczanie jamek trawienia uzyskiwanych przy zastosowaniu metody selektywnego trawienia lub metod rentgenowskich.
Ilościowe badania umocnienia materiału warstwy wierzchniej przeprowadza się w zasadzie przez zastosowanie metod pomiaru mikrotwardości. Na podstawie różnicy mikrotwardości materiału nieodkształconego i odkształconego wnioskuje się o wartości umocnienia. Z wielu znanych metod pomiaru mikrotwardości (metoda: ryskowa, strugania, wciskania penetratora i inne) do badania wartości umocnienia stosuje się w zasadzie tylko metodę wciskania penetratora. Duże rozpowszechnianie i wysoka dokładność pomiarów mikrotwardości metodą wciskania penetratora Vickersa lub Knoopa czyni je najbardziej przydatnymi do badania umocnienia warstwy wierzchniej. Wartości obciążeń wciskających penetrator Vickersa lub Knoopa zawierają się w zakresie 0,49-1,96 N (5-200 G).
Mikrotwardość materiału warstwy wierzchniej mierzoną metodą V i c k e r s a oblicza się z zależności
gdzie: P - siła obciążająca w N, a = ½ (a1 + a2) - przekątne odcisku w µm.
Przy pomiarach mikrotwardości obowiązuje prawo Mayera, ponieważ istnieje różnica między charakterem odkształcenia badanego materiału pod wierzchołkiem ostrosłupa i pod jego krawędziami. Uwzględnianie tej różnicy przy pomiarze, zwłaszcza gradientu umocnienia warstwy wierzchniej badanego materiału na skośnym zgładzić, ma bardzo duże znaczenie, ponieważ do tego celu stosuje się małe obciążenie penetratora (małe zagłębienie ostrosłupa). Im mniejsze zagłębienie ostrosłupa w badanym materiale warstwy wierzchniej, tym wpływ różnicy odkształcenia materiału na dokładność pomiaru mikrotwardości pod wierzchołkiem ostrosłupa i pod jego krawędziami jest większy.
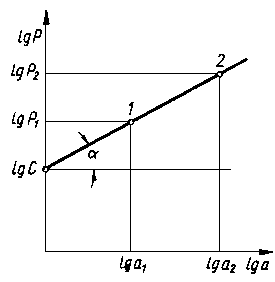 |
Rys. 3.32. Wykres równania lgP = lgC + nlga
|
Wartość współczynnika n (rys. 3.32) przy pomiarze mikrotwardości ostrosłupem Vickersa nie jest stałą materiału, lecz zmienia się wraz z wartością obciążenia użytego do wciśnięcia wgłębnika. Im większa jest wartość obciążenia, tym bardziej wartość współczynnika Mayera zbliża się do 2 (przy obciążeniach penetratora Vickersa w zakresie makrotwardości n = 2).
Praktycznie można przyjąć, że w zakresie obciążeń 0,49-1,96 N (5-200 G) wielkość n jest stała dla danego materiału. Wartości n są na ogół większe dla materiałów miękkich, a mniejsze dla materiałów twardych. Stan umocnienia materiału w warstwie wierzchniej jest szacowany ilościowo w skali względnej i dlatego można zaniedbać wpływ wymienionych czynników na dokładność pomiaru przy założeniu, że badania przeprowadzono przy jednakowym obciążeniu wgłębnika.
Mikrotwardość jest określona wzorem
|
HV = 1854,4 c a n-2
| (3.116)
|
przy czym wartość stałych c i a oblicza się z zależności
|
ln P = ln c + n ln a
| (3.117)
|
wykreślając prostą tego równania we współrzędnych P-a w układzie podwójnie logarytmicznym. Tangens nachylenia prostej względem osi jest równy wartości współczynnika n. Wykonując w badanym materiale pod obciążeniem dwa odciski wgłębnikiem Vickersa uzyskuje się dane do obliczenia wartości n
|
n = |
ln P2 - ln P1
ln a2 - ln a1
| (3.118)
|
Znacznie większą dokładność pomiaru umocnienia materiału warstwy wierzchniej uzyskuje się przy pomiarze mikrotwardości piramidką K n o o p a. Pomiar mikrotwardości metodą Knoopa polega na wciskaniu w badany materiał ostrosłupa o podstawie rombu. Linia przenikania ostrosłupa Knoopa z płaszczyzną prostopadłą do osi tego ostrosłupa jest rombem, o stosunku przekątnych l/a = 7,114 gdzie: l - dłuższa przekątna, a - krótsza przekątna.
Miarą twardości materiału wg Knoopa jest stosunek obciążenia wgłębnika do powierzchni rzutu odcisku
gdzie: P - obciążenie penetratora w N, l - długość większej przekątnej w µm.
Metoda Knoopa zapewnia uzyskanie znacznie większej dokładności pomiaru niż metoda Vickersa. Ponadto przy tym samym obciążeniu zagłębienie wgłębnika Knoopa w materiał jest znacznie mniejsze niż wgłębnika Vickersa i dlatego metoda Knoopa jest przydatna zwłaszcza przy badaniu gradientu umocnienia warstwy wierzchniej na skośnym zgładzić. Przy takiej samej wartości obciążenia penetratorów Vickersa i Knoopa (rys. 3.33) wartość dłuższej przekątnej w metodzie
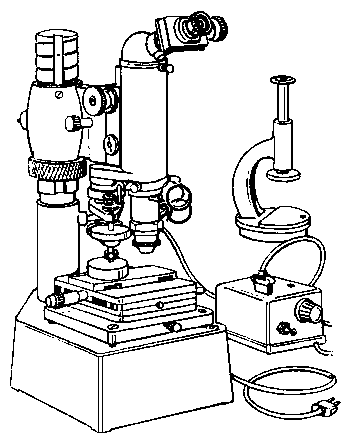 |
Rys. 3.33. Mikrotwardościomierz PMT-3
|
Knoopa jest większa niż w metodzie Vickersa, a więc w metodzie Knoopa popełnia się procentowo mniejszy błąd niż w metodzie Vickersa. Przy pomiarze mikrotwardości metodą Knoopa dłuższa przekątna nie zmienia się w wyniku odkształceń sprężystych materiału po odciążeniu ostrosłupa i dlatego dokładność pomiaru jest większa. Za pomocą tej metody można określać izotropowość krystalitów w badanym materiale warstwy wierzchniej.
3.5.3.3. Metody badania zmian strukturalnych materiału warstwy wierzchniej
W warstwie wierzchniej mogą następować zmiany struktury elektronowej pierwiastków, struktury kryształów i struktury fazowej.
Strukturę elektronową i strukturę kryształów bada się metodami rentgenowskimi (metody analizy strukturalnej). Interpretację rentgenogramów przeprowadza się porównując je ze wzorcami struktur. Struktury fazowe (mikrostruktury) bada się natomiast za pomocą mikroskopu optycznego lub elektronowego. Określenie faz lub składników strukturalnych przeprowadza się zarówno pod względem ilości, rozkładu, kształtu i wielkości, jak i innych parametrów związanych z przebiegiem procesów formujących strukturę warstwy wierzchniej. Mikrostrukturę warstwy wierzchniej bada się za pomocą techniki metalograficznej na zgładach ukośnych lub cienkich.
Na skośnym zgładzić można obserwować struktury przy użyciu mikroskopu optycznego (metalograficznego) lub elektronowego, po sporządzeniu odpowiednich replik. Faza jest oddzielona od reszty metalu powierzchnią rozdziału (granica faz) i stosuje się do praw reguły Gibbsa. Przy zastosowaniu techniki mikroskopowej można badać także fazy międzymetaliczne i poszczególne składniki strukturalne.
Rozkład faz i składników strukturalnych może być równomierny, nieregularny, sporadyczny lub skupiony w określonych miejscach poprzecznego przekroju warstwy wierzchniej, np. wskutek segregacji, likwidacji i rozkładu warstwowego. Warstwy submikroskopowe i mikrostruktury bada się przy użyciu mikroskopu elektronowego, z zastosowaniem techniki replik lub techniki rozpraszania elektronów przechodzących przez cienką folię badanego metalu.
Przygotowanie zgładów w stadiach początkowych (pobieranie próbek, szlifowanie, polerowanie) jest identyczne w metalografii optycznej, jak i elektronowej. Szczególnej uwagi wymaga trawienie oraz czyszczenie powierzchni próbki po trawieniu. Próbki powinno się polerować mechanicznie, ale bardzo starannie, aby przy obserwacji pod mikroskopem optycznym w polu ciemnym, przy powiększeniu 500 x, nie było widać rys. Miękkie metale poleruje się elektromechanicznie, ponieważ wygładzanie mechaniczne pozostawia rysy. Polerowanie elektrochemiczne zniekształca obszary wokół wtrąceń oraz pozostawia nierówności. Przy polerowaniu mechanicznym należy usunąć przed ostatecznym trawieniem warstwę Beilbye'go.
Zgłady można trawić chemicznie lub elektrochemicznie. Rzadziej stosuje się trawienie cieplne przez odparowywanie w próżni lub bombardowanie jonowe powierzchni w gazach rozrzedzonych. Rodzaj odczynnika, jego stężenie i czas działania ustala się praktycznie w zależności od rodzaju badanego materiału, jego struktury i celu badania.
Ogólnie biorąc, do celów metalografii elektronowej są stosowane odczynniki, których selektywne oddziaływanie na poszczególne fazy wyraża się przede wszystkim różnicą w szybkości reakcji, a przez to wystąpieniem wyraźnego reliefu powierzchni.
Na przedmiotach trawionych nie mogą zostawać po przemyciu produkty reakcji chemicznej, ponieważ zacierają one obraz struktury. Ze względu na wierność odtwarzania powierzchni oraz łatwość oddzielania repliki od zgładu wskazane jest słabe trawienie. W badaniach metalografii optycznej powierzchnię zgładu należy trawić intensywniej.
W celu określenia właściwej głębokości trawienia są stosowane różne czasy dla danego rodzaju metalu. Ogólnie najkorzystniejszy relief uzyskuje się, jeżeli czas działania odczynnika jest o 20% krótszy od czasu stosowanego do badań metalograficznych na mikroskopie optycznym. Przy stosowaniu replik organicznych głębokość reliefu może być taka sama, jak przy badaniach na mikroskopie optycznym. Kontrast osłabiony słabym trawieniem wzmacnia się przez cieniowanie replik. Czas działania oraz skład chemiczny odczynnika przy trawieniu powinien być (zwłaszcza przy badaniach porównawczych) taki sam. W przypadku stali węglowej i niskostopowej stosuje się następujące odczynniki:
a) dla struktur perlitycznych i perlityczno-ferrytycznych stosuje się 2-proc. roztwór HNO3 w alkoholu n - amylowym; odczynnik ten, skłonny do wytwarzania błonek tlenkowych, rozpuszcza cementyt i dlatego nie zawsze jest stosowany; drugim odczynnikiem jest roztwór kwasu pikrynowego w alkoholu metylowym lub etylowym chemicznie czystym; odczynnik ten daje bardzo wyraźne kontrasty struktury ferrytyczno-cementytowej;
b) dla struktur ferrytycznych stosuje się odczynnik o składzie l g FeCl3+2 cm³ HCl (r = 1,21 g/cm³) na 100 cm³ CH3OH - chemicznie czystego; odczynnik trawi powierzchnię ferrytu ułatwiając ustalenie orientacji krystalograficznych w ziarnach;
c) dla struktur beinitycznych stosuje się odczynnik o składzie l g CuCl2 kryst.+2 cm³ HCl na 100 cm³ CH3OH;
d) dla zróżnicowania węglików w stalach stopowych stosuje się odczynnik o składzie 4 g KMnO4 + 6g NaOH na 100 cm³ wody destylowanej.
Działanie powyższych odczynników można modyfikować przez dodatek niewielkich ilości substancji powierzchniowo-aktywnych, np. chlorku zefiranu (chlorek alkilodwumetylobenzylaminowy). Bezpośrednio po trawieniu usuwa się resztki odczynnika trawiącego i produkty trawienia, płucząc powierzchnię zgładu. Odczynniki używane do płukania nie mogą powodować zmian powierzchni. Do płukania stosuje się następujące kąpiele (stosowane kolejno):
1) 49% acetonu + 50% alkoholu metylowego + 1% kwasu cytrynowego lub mrówkowego,
2) 50% acetonu+50% alkoholu metylowego,
3) benzen chemicznie czysty.
Następnie próbkę suszy się w strumieniu ciepłego powietrza. Powierzchnię zgładu po trawieniu czyści się replikami czyszczącymi. Repliki czyszczące usuwają pozostałe ślady produktów reakcji po trawieniu oraz częściowo wyizolowane z osłony wtrącenia, które mogą odrywać się od powierzchni wraz z repliką. Oczyszczanie polega na wykonaniu jednego lub dwóch replik łąkowych, które oddzielają od powierzchni zanieczyszczenia. Repliki czyszczące są grubymi błonkami naniesionymi na powierzchnię zgładu z gęstego roztworu nitrocelulozy w octanie amylowym, formwaru w chloroformie lub innych podobnych roztworów. Po wysuszeniu utworzoną błonkę oddziela się od zgładu obcinając jej brzegi na powierzchniach przyległych, a następnie zanurza się próbkę w naczyniu z wodą destylowaną, z dodatkiem NH4OH (przeciwdziała korozji), repliką czyszczącą ku górze. Po 15 ¸ 30 min można łatwo zdjąć replikę, podważając brzegi pincetą.
Zamiast stosować poprzednio opisaną metodę można replikę zdjąć zanurzając ją kilkakrotnie na przemian w gorącej (95°C) i zimnej (18°C) wodzie destylowanej wytrzymując po 5 s. Wskutek różnicy temperatury replika się kurczy i rozszerza, osłabiając spójność ze zgładem i umożliwiając jej oderwanie od zgładu.
Po zdjęciu repliki czyszczącej powierzchnia zgładu powinna być osuszana w strumieniu ciepłego powietrza. Jeżeli nie nakłada się natychmiast repliki właściwej, wówczas powinno się zabezpieczyć zgład przed wpływami atmosferycznymi, nakładając replikę kolodionową ochronną. Replika ochronna może być uważana za drugą replikę czyszczącą. Próbki z replikami ochronnymi przechowuje się w eksykatorze z pochłaniaczem wody.
W przypadku inkludowania próbek dobiera się taką masę inkludującą, aby była ona odporna na działanie odczynników trawiących, myjących i rozpuszczających materiały stosowane na repliki (np. żywica melaminowo-formaldehydowa). Tak przygotowane zgłady skośne pod kątem około 3° można obserwować pod mikroskopem optycznym. Natomiast w przypadku mikroskopu elektronowego wykonuje się repliki właściwe z kolodium, formwaru, mowitalu oraz jednostopniowe matrycowe repliki węglowe.
Repliki tlenkowe umożliwiają bardzo wierne odtworzenie powierzchni zgładu nawet bez uprzedniego trawienia, ponieważ utleniona warstewka powierzchniowa badanego metalu ściśle do niej przylega. Badaną powierzchnię można utlenić elektrolitycznie (eloksalowanie, anodyzacja Al). Anodą jest badana próbka, a katodą - węgiel lub platyna zanurzona w elektrolicie, stanowiącym 3-proc. roztwór wodny cytrynianu lub boranu.
Po rozpuszczeniu kwasu cytrynowego dodaje się NH4OH aż do uzyskania 8 ¸ 9 pH. Grubość warstewki tlenków w zależności od napięcia na elektrodach oblicza się z zależności podanej przez Nagelsa [18]. Przy zastosowaniu replik tlenkowych nie wymaga się na ogół zwiększania kontrastu i po wysuszeniu nadają się one do obserwacji. Można również utleniać powierzchnie badane w stopionych solach azotanowych.
Metoda utleniania chemicznego w niskich temperaturach została opisana przez J. Nuttinga [18].
Przy replikach jednostopniowych badana struktura jest odwzorowana na warstewce obcej, wypełniającej wszelkie nierówności reliefu, która po oddzieleniu służy za preparat mikroskopowy. Warstewki można otrzymać przez wysuszenie naniesionych na powierzchnię zgładu rozcieńczonych roztworów żywic organicznych, naparowanie w próżni metalem, węglem lub tlenkiem krzemu.
Repliki plastyczne są łatwe do wykonania, dając obrazy zbliżone do uzyskiwanych pod mikroskopem optycznym, a zatem ułatwiają interpretację zdjęć, ale rozdzielczość ich obrazów jest mała (30 nm). Błonki z reguły wykonuje się z nitrocelulozy rozpuszczonej w octanie amylowym, z formwaru rozpuszczonego w chloroformie chlorku etylenu lub dioksanie oraz z mowitalu F rozpuszczonego w chloroformie. Dość mała wytrzymałość mechaniczna tych replik zmusza do stosowania błonek grubych (80 nm), co pogarsza rozdzielczość obrazu. Ponadto błonki te mają strukturę wewnętrzną widoczną przy większych powierzchniach. Repliki z 0,5 ¸ 1,0-proc. roztworem nitrocelulozy w octanie amylu są zbyt cienkie i mało wytrzymałe.
Repliki formwarowe o stężeniu 0,5% w chloroformie są stosowane z powodzeniem do struktur ferrytycznych. Dla grubszych struktur przy oddzielaniu suchym można stosować stężenie 2 ¸ 2,5%. Repliki formwarowe są bardziej wytrzymałe od nitrocelulozowych, ale nieco gorzej odtwarzają szczegóły struktur.
Repliki mowitalowe rozpuszczone w chloroformie o stężeniu 0,7% zapewniają uzyskanie dość dobrych kontrastów, przy czym ich wytrzymałość jest zadowalająca. Oddzielenie wyżej omówionych replik od zgładu można przeprowadzić wieloma sposobami.
Oddzielanie suche polega na nalepianiu odcinka gumowej taśmy celofanowej na replikę. Po pewnym czasie odrywa się taśmę razem z repliką. Następnie nacina się na replice kwadraty o boku 3 mm i zanurza cały odcinek taśmy w wodzie o temperaturze 40°C. Kawałki repliki oddzielają się od taśmy i wypływają na powierzchnię wody, gdzie są „chwytane" na nośnik preparatu i suszone. Metoda może mieć zastosowanie przy niezbyt głębokim trawieniu i mało skomplikowanej strukturze.
Oddzielanie w wodzie przeprowadza się wykorzystując skłonność wody do wciskania się między replikę a zgład. Próbkę wraz z repliką zanurza się w wodzie o temperaturze około 40°C i pincetą odciąga replikę powoli od zgładu. Podobnie jak przy oddzieleniu suchym może nastąpić zdeformowanie i zniekształcenie repliki oraz odrywanie cząstek metalu lub wtrąceń związanych z repliką. Z tego względu należy repliki myć w rozcieńczonych kwasach (10 ¸ 20-proc HC1, H2SO4, HNO3) w ciągu l godziny, a następnie płukać w wodzie destylowanej.
Oddzielanie ze wzmocnieniem nie powoduje deformacji repliki przy oddzielaniu jej od zgładu. Replika złożona (replika + błonka wzmacniająca) jest gruba i łatwo można ją oddzielić stosując metodę jak przy replikach czyszczących. Błonki wzmacniające wykonuje się z roztworów żywic nie działających na repliki, np. z polistyrenu w benzenie lub nitrocelulozy włącznie z replikami formwarowymi i mowitalowymi.
W praktyce stosuje się najczęściej 15 ¸ 20-proc. roztwór nitrocelulozowy w octanie amylu. Replikę suszy się dokładnie, ponieważ w przeciwnym przypadku po oddzieleniu jej od zgładu ma ona tendencję do zwijania się. Po oddzieleniu repliki rozcina się ją na kwadraciki o boku 3 mm i nakłada stroną wzmocnioną na nośnik, zanurzając następnie w odpowiednim rozpuszczalniku, w celu usunięcia błonki wzmacniającej (rys. 3.34).
Oddzielanie chemiczne polega na zanurzeniu próbki z naciętą siatką 3x3 mm repliki w roztworze i wytrzymaniu jej tak długo, aż repliki zaczną odstawać od zgładu.
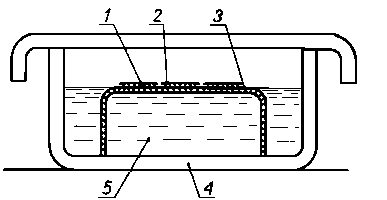 |
Rys. 3.34. Urządzenie do rozpuszczania błonek wzmacniających i matryc;
- - siatka (nośnik),
- - replika dwustopniowa,
- - siatka niklowa,
- - naczynie szklane,
- - rozpuszczalnik
|
Następnie bardzo ostrożnie zanurza się próbki w wodzie destylowanej, w której następuje całkowite oddzielenie replik. Repliki przemywa się w 10-proc. roztworze HC1, a następnie w wodzie destylowanej. Czyste repliki umieszcza się na nośniku preparatu i razem suszy się bardzo ostrożnie, aby nie popękały.
Oddzielenie elektrochemiczne jest oparte na tej samej zasadzie co chemiczne i technologia obróbki repliki jest identyczna, tylko mechanizm osłabienia powiązania repliki ze zgładem jest oparty na przepływie prądu.
Oddzielenie za pomocą żelatyny nie powoduje niszczenia zgładu, ale sprzyja deformacji repliki. Proces jest podobny jak przy oddzieleniu replik złożonych, z błonkami wzmacniającymi.
Kontrast w obrazie mikroskopowym w przypadku replik plastycznych powstaje na skutek różnic w grubości błonki w różnych obszarach zgładu. Im głębszy relief struktury i im cieńsza replika, tym kontrasty są większe, ale ogólnie repliki plastyczne dają słabe kontrasty, dlatego powinny być cieniowane.
Repliki metalowe bezpośrednio prawie nie są używane ze względu na własną strukturę krystaliczną powodującą interferencję promieni rozpraszanych przez preparat oraz trudne oddzielenie błonek od zgładów. Repliki metalowe ze względu na intensywne pochłanianie elektronów muszą być bardzo cienkie (2 ¸ 3 nm) i w związku z tym są mało wytrzymałe. Metale Al, Be napyla się w próżni rzędu 0,133 • 10 -5 kPa. Parownikiem jest W lub Mo.
Oddzielanie repliki od zgładu przeprowadza się najczęściej elektrolitycznie, w roztworze H2SO4, przy czym próbka jest włączona w obwód jako anoda.
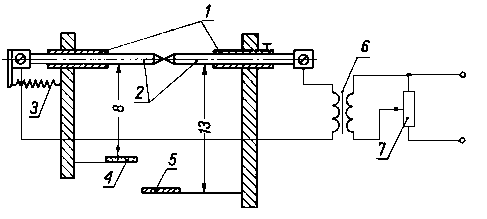 |
Rys. 3.35. Urządzenie do napylania replik metodą Bradleya;
- - obudowa elektrod,
- - elektrody,
- - sprężyna dociskowa elektrod,
- - uziemienie,
- - uziemienie,
- - transformator,
- - regulator oporu
|
Polega ono na napyleniu na powierzchnię kontaktową zgładu (przed napyleniem właściwej repliki) B2O3 o grubości o 5 nm. Materiały do odparowania muszą być chemicznie czyste i nie mogą koagulować.
Repliki węglowe, jak i kwarcowe, umożliwiają uzyskanie najwyższej rozdzielczości, rzędu 2 ¸ 3 nm. Odporne są one chemicznie, bardzo trwałe przy obserwacji w mikroskopie i względnie łatwe w preparowaniu ze względu na dobrą wytrzymałość i widoczność. Napylanie węgla prowadzi się metodą Bradley'a (rys. 3.35). Pary węgla powstałe w miejscu zetknięcia w próżni dwóch elektrod węglowych odpowiednio „zarobionych", przez które płynie prąd o dużym natężeniu 50 A/cm², osadzają się na zgładzie. W celu określenia grubości napylonej repliki stosuje się odpowiedni indykator (biała płytka porcelanowa) ustawiony obok preparatu. Barwa nalotu na płytce porcelanowej charakteryzuje grubość napylonej repliki. W celu łatwiejszej oceny grubości warstwy repliki na płytce porcelanowej umieszcza się kroplę oleju próżniowego, np. barwa jasnożółta odpowiada grubości repliki około 5 nm. Zazwyczaj repliki węglowe mają grubość 20 ¸ 30 nm (barwa jasnobrązowa).
Napylanie odbywa się w kierunku normalnym do powierzchni zgładu, przy czym bardzo istotne jest utrzymanie wymaganej próżni, rzędu 0,133 • 10 -5kPa, ponieważ stosunkowo lekkie atomy węgla w przypadku niezbyt wysokiej próżni, napotykając na swej drodze cięższe cząsteczki tlenu i azotu, zostają rozproszone. Wskutek tego pojawiają się na replice lokalne zgrupowania węgla, powodujące dodatkowe efekty na błonie fotograficznej. Z tego też względu odległość między napyloną powierzchnią a źródłem emisji powinna być nie większa niż 100 mm. W praktyce elektrodami są pałeczki grafitowe używane w spektografii, o średnicy 5 mm, dociśnięte sprężyną. Napylanie przeprowadza się w urządzeniu do cieniowania (w napylarce) z zastosowaniem uchwytów do elektrod węglowych. Dobre rezultaty uzyskuje się napylając nie prostopadle do powierzchni, lecz pod pewnym kątem (cieniowanie pod dwoma kątami). Metoda ta umożliwia uzyskanie lepszej plastyczności obrazu (samocieniowanie).
Technologia wykonywania replik kwarcowych jest identyczna do technologii wykonywania replik węglowych. Repliki kwarcowe mają mniejszą wytrzymałość i gorszą widoczność w cieczach, wskutek czego wymagają przy nakładaniu na nośniki specjalnego rodzaju oświetlenia. Grubość warstewki kwarcu powinna wynosić 40 ¸ 60 nm; reguluje się przez odpowiednie dawkowanie ilości kwarcu przeznaczonego do odparowania albo przez eksperymentalne ustalenie czasu i parametrów prądu. Jednostopniowe repliki kwarcowe zapewniają uzyskanie najlepszych wyników przy badaniu stopów jednofazowych, przy niezbyt głębokim trawieniu. Repliki SiO charakteryzują się wysoką zdolnością rozdzielczą, odpornością na działanie strumienia elektronów oraz odpornością chemiczną, termiczną i mechaniczną. Umożliwiają one odtworzenie struktury, której szczegóły są mniejsze od cząsteczek tworzywa repliki (rzędu 10 nm).
Repliki ekstrakcyjne są stosowane przy badaniu metalograficznym struktur zawierających wtrącenia węglików, faz międzymetalicznych itp. Stosuje się tu specjalne metody, aby wyekstrahować wydzielenia wraz z repliką i w ten sposób otrzymać w obrazie mikroskopowym dokładny kontrast, wielkość i rozmieszczenie wydzieleń w strukturze z możliwością ich analizy przez badania dyfrakcyjne.
Proces wykonywania replik dwustopniowych polega na wykonaniu matrycy odtwarzającej relief powierzchni próbki, na którą nanosi się replikę właściwą.
Przy starannym wykonaniu matryc niewiele zmniejsza się rozdzielczość replik, natomiast łatwiejsze jest oddzielenie ich od zgładu, który może być wtedy wykorzystany kilkakrotnie. Obrazy z matryc są łatwiejsze do interpretacji, ponieważ replika jest kopią, a nie negatywem powierzchni.
Matryce wykonuje się jako:
- błonki elastyczne (nitroceluloza, formwar) o grubości 0,2 ¸ 0,3 mm,
- metaliczne warstwy naparowane (Ag, Al),
- prasowane termoplastycznie (polistyren, celuloid) lub w temperaturze otoczenia (aluminium, triafol),
- polimeryzacja z polimetakrylu z dodatkiem kilku procent opóźniacza.
Po oddzieleniu matrycy od zgładu wytwarza się na niej właściwą replikę, najczęściej przez naparowanie węgla, kwarcu lub metalu. Przed naparowaniem można matrycę cieniować. Następnie oddziela się replikę, najczęściej rozpuszczając matrycę w odpowiednim rozpuszczalniku.
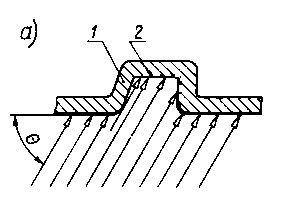
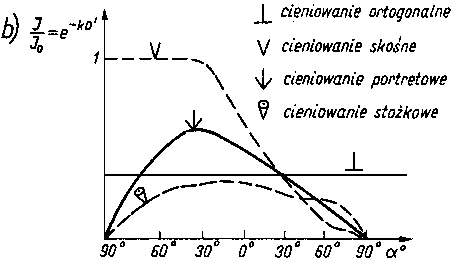
Cieniowanie wprowadza się jako sposób zwiększenia kontrastu i rozdzielczości replik plastycznych oraz w niektórych przypadkach innych replik dających obrazy trudne do interpretacji. Cieniowanie polega na pokryciu replik od strony reliefu nierównomierną warstwą, najczęściej metalu naparowanego w próżni (rys. 3.36a). Nierównomierność uzyskuje się przy ustawieniu replik pod kątem względem parownika (rys. 3.36).
 | 
|
Rys. 3.36. Cieniowanie replik:
- schemat cieniowania,
- zależność względnej intensywności osadzania materiału od kąta cieniowania Q;
- - replika,
- - cienie na replice.
- J, Jo - intensywność promieniowania
|
Kąt cieniowania powinien wynosić 15° dla struktur z drobnymi wydzieleniami, natomiast do 45° dla struktur perlitycznych. Do cieniowania stosuje się metale o dużej masie atomowej (Au, Pt, Cr, U), nie koagulujące, nie ulegające kondensacji zbiorczej przy naparowaniu oraz nie rekrystalizujące przy ogrzaniu w mikroskopie. Element grzejny parownika jest wykonany z drutu lub blachy wolframowej, molibdenowej albo tantalowej, w zależności od rodzaju odparowywanego pierwiastka.
Grubość warstewki cieniującej określa się na podstawie obserwacji koloru indykatora. Stosuje się również cieniowanie reliefu przed nałożeniem repliki, przez co uzyskuje się większą rozdzielczość obrazu. Metoda ta sprawia duże trudności w oddzielaniu błonek od zgładu. Można tego uniknąć przez wytworzenie na powierzchni zgładu cienkiej warstewki związków powierzchniowoaktywnych, tworzących zorientowane warstwy monomolekularne. Prowadzi się także cieniowanie portretowe, które polega na tym, że preparat cieniowany z jednej strony zostaje obrócony o 180° i jeszcze raz jest cieniowany z tego samego źródła. Czas cieniowania preparatu po jego obróceniu jest znacznie krótszy (ponieważ należy nanieść 1/7 grubości warstwy otrzymanej przy cieniowaniu przed obróceniem). Przy tej metodzie uzyskuje się bardzo wyraźny i plastyczny obraz.
Przy cieniowaniu stożkowym preparat w czasie cieniowania obraca się z dużą prędkością kątową wokół swojej osi.
Kontrastem nazwano stosunek intensywności strumienia elektronów po przejściu przez warstwę cieniowaną do intensywności strumienia przed przejściem przez tę warstwę.
Cieniowanie stożkowe jest jakby sumą nieskończonej ilości cieniować skośnych. Między zdolnością rozdzielczą a gęstością cieniującego metalu istnieje zależność podana w pracy [12].
Badając strukturę warstwy wierzchniej staramy się ujawnić nowe szczegóły, stosując podczas obserwacji odpowiednie powiększenia. W tym przypadku decydującą rolę ma zdolność rozdzielcza preparatu i mikroskopu. Mikroskop optyczny daje maksymalne powiększenie około 2000 x i dalsze fotograficzne powiększenie nie wnosi nowych szczegółów. Mikroskop elektronowy zapewnia uzyskiwanie dużych powiększeń, rzędu 300 000 x, przy czym powiększenia fotograficzne często polepszają czytelność obrazu. Gradient zmian strukturalnych w przekroju poprzecznym może być precyzyjnie określony na podstawie zdjęć wykonanych w mikroskopie elektronowym.
W celu obserwacji pod mikroskopem elektronowym wybranego miejsca na zgładzie, miejsce na zgładzie lub replice zaznacza się za pomocą rysika, wstawionego do mikroskopu optycznego w miejscu obiektywu, lub rysy zrobionej na mikrotwardościomierzu.
Oznaczone miejsce ustawia się na środku siateczki nośnika preparatu lub na diafragmie o jednym otworze i małej średnicy otworu. Trudno jednak umieścić dany szczegół pod mikroskopem stereoskopowym w otworze diafragmy. Dlatego też nakłada się na obiektyw (wykonaną z masy plastycznej) tulejkę, do której przylepia się replikę. Po znalezieniu danego miejsca opuszcza się obiektyw na tulejkę, aż do zetknięcia z repliką. Matryca przylepia się do tulejki i zostaje wraz z nią podniesiona, a diafragma położona centrycznie na stoliku mikroskopu. Na brzegu diafragmy znajduje się klej, do którego przylepia się replika.
Przy badaniu w mikroskopie elektronowym warstwy wierzchniej bardzo duże znaczenie ma tzw. „preparatyka celowana”, ponieważ przy obserwacji skośnych zgładów dokładniej ona orientuje, które miejsce na zgładzić znajduje się w polu obserwacji mikroskopowej.
Wszystkie metody sporządzania replik mogą być wykorzystane przy badaniu warstwy wierzchniej, jednak repliki matrycowe zapewniają uzyskanie najlepszych wyników.
Badania zmian strukturalnych w cienkich zgładach nie zapewniają uzyskania zadowalających wyników, ponieważ technika przygotowania cienkiego zgładu powoduje duże zmiany w warstwie badanego metalu, zakłócające wytworzony stan struktury warstwy wierzchniej.
Cienki zgład warstwy wierzchniej wykonuje się w następujący sposób. Najpierw usuwa się rdzeń materiału przez szlifowanie i polerowanie mechaniczne, a następnie poleruje się elektrochemicznie powierzchnię warstwy wierzchniej od strony granicy wewnętrznej.
Cienkie zgłady lub odpowiednio sporządzoną replikę skośnego zgładu warstwy wierzchniej obserwuje się w mikroskopie elektronowym (rys. 3.37).
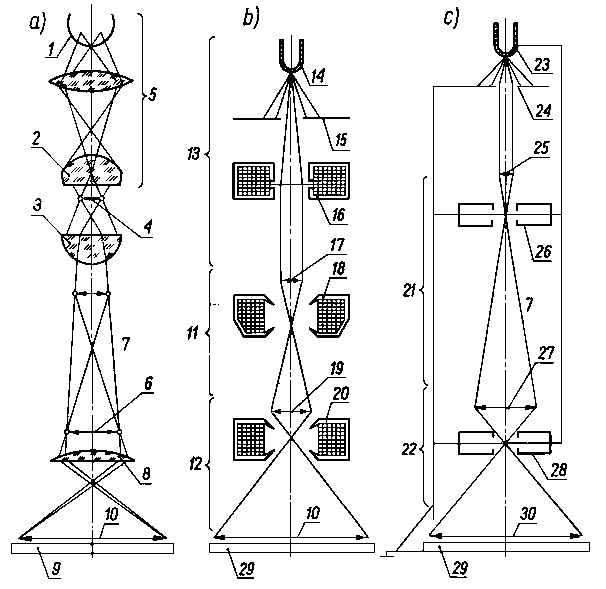 |
Rys. 3.37. Modele działania mikroskopów:
- Optycznego,
- elektronowego magnetycznego,
- elektronowego elektrostatycznego,
- widok mikroskopu elektronowego;
1,14, 23-włókno żarowe,
2, 16 - kondensator,
3, 18, 26 - obiektyw,
4, 17, 25 - przedmiot,
5, 13 - urządzenia oświetlające,
6, 19, 27 - obraz pośredni,
7 - tubus,
8, 20, 28 - okular,
9, 29 - płyta fotograficzna,
10, 30 - obraz powiększony,
11, 21 - układ powiększający I,
11, 22 - układ powiększający II,
15, 24 - przysłona
|
3.5.3.4. Metoda badania fragmentacji krystalitów warstwy wierzchniej
Jeśli w wyniku obróbki cieplnej zostaną usunięte naprężenia własne w warstwie wierzchniej, wówczas głównym czynnikiem charakteryzującym własności mechaniczne metalu tej warstwy jest wielkość ziarn. Zmniejszenie wymiarów ziarn w warstwie wierzchniej elementów maszyny następuje w wyniku ich łamania podczas obróbki mechanicznej lub eksploatacji. Na ogół zmniejszeniu (rozdrobnieniu) ziarn towarzyszy wzrost twardości materiału warstwy wierzchniej. Im mniejsza jest średnica ziarn materiału warstwy wierzchniej, tym mniejsza jest jego plastyczność, większa wartość granicy plastyczności, większa twardość, materiał intensywniej się umacnia oraz maleje chropowatość powierzchni złomu.
Wielkość ziarna materiału warstwy wierzchniej można zmierzyć stosując metody optyczne lub rentgenowskie.
Metody optyczne polegają na tym, że polerowany i wytrawiony zgład metalograf iczny jest obserwowany pod mikroskopem przy odpowiednim powiększeniu. Gradient zmian rozdrobnienia ziarn materiału warstwy wierzchniej jest badany metodami optycznymi i rentgenowskimi na skośnym zgładzić.
Wielkość ziarna ocenia się metodami optycznymi w ten sposób, że mierzy się średnicę poszczególnych ziarn w polu widzenia pod mikroskopem lub liczbę ziarn w l mm². Można również podawać średnią powierzchnię ziarna w mm² lub według klasyfikacji JKM albo ASTM. W tabl. 3.4 podano współzależności między wymiarami ziarn ocenianymi różnymi metodami.
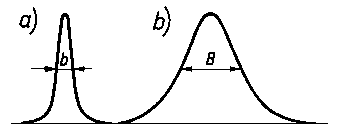 |
Rys. 3.38. Rentgenogramy proszkowe krystalicznego kwarcu z różnymi wymiarami ziarn:
- duże ziarna,
- małe ziarna
|
W przypadku ziarn mniejszych niż 10 -4 (rys. 3.38) powstaje rozszerzenie linii fotometrycznej (rozmycie linii). Opierając się na teorii dyfrakcji można z obserwacji rozszerzenia linii dyfrakcyjnej obliczyć statystyczny rozkład ziarn (krystalitów) według ich wymiarów (rys. 3.39).
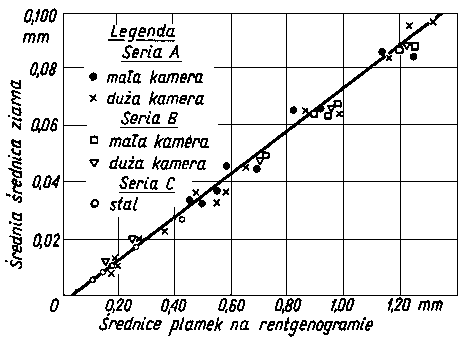 |
Rys. 3.39. Zależność pomiędzy wymiarami plam dyfrakcyjnych a średnią średnicą ziarna
|
3.5.3.5. Metoda badania steksturowania warstwy wierzchniej
W celu zbadania tekstury warstwy wierzchniej stosuje się metody badań umożliwiające wyznaczenie anizotropii krystalitów metalu.
Steksturowanie warstwy wierzchniej można dokładnie zbadać rentgenograficznie. Jeśli równoległą wiązkę promieni rentgenowskich o długości fali ), skieruje się na powierzchnię badanej warstwy wierzchniej niesteksturowanej, to w każdym przypadku w badanej warstwie będzie wystarczająca ilość płaszczyzn krystalograficznych spełniających równanie Bragga
gdzie: A-długość fali promieniowania rentgenowskiego w nm, d - odległość między płaszczyznowa w nm, QB - kąt odbłysku (Bragga), n - liczba całkowita.
Ugięta wiązka promieni rentgenowskich tworzy stożek wokół osi, którą jest wiązka pierwotna. Kąt rozwarcia stożka wynosi 2Q. Połowa kąta rozwarcia stożka ma dla każdej płaszczyzny sieciowej wartość d dlatego powstaje kilka stożków interferencyjnych. Jeśli na drodze promieni ugiętych ustawi się prostopadle do nich błonę filmową, wówczas jako ślady przecięcia tych promieni z płaszczyzną powstają pierścienie Debye'a-Scherrera (rys. 3.40).
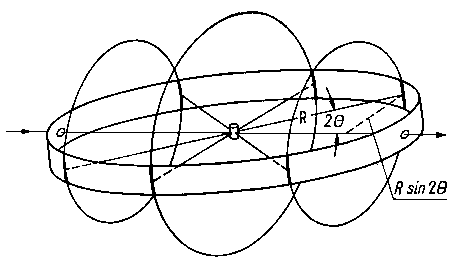 |
Rys. 3.40. Model przecinania stożka interferencyjnego z błoną fotograficzną w metodzie Debye'a-Scherrera
|
Przy uginaniu promieni rentgenowskich przez próbkę drobnoziarnistą o statystycznie nieuporządkowanych kierunkach krystalograficznych zaczernienie błony filmowej (prążek) jest równomierne. Jeśli jednak istnieją pewne prawidłowości w rozmieszczeniu i uprzywilejowaniu niektórych kierunków krystalograficznych (steksturowanie), wtedy ugięte promienie rentgenowskie w takim metalu spowodują lokalne zaczernienia prążka i jednocześnie rozjaśnienia na pozostałym obwodzie.
Długość zaczernionych łuków jest zależna od szerokości pokrytego obszaru na tzw. kuli projekcji przestrzennej; próbkę umieszcza się w środku tej kuli i przeprowadza proste prostopadłe do płaszczyzn sieciowych próbki. Proste prostopadłe przebijają kulę projekcji wzdłuż koła refleksji (ugięcia promieni rentgenowskich). Odległość tego koła od promienia pierwotnego wynosi 90-Q. Jeśli istnieje dużo uginających płaszczyzn sieciowych, to prostopadłe do tych płaszczyzn wypełniają równomiernie koło refleksji, co jest równoznaczne z równomiernym zaczernieniem koła debejowskiego.
Tabela 3.4
Zależność między wymiarami ziarn badanych różnymi metodami | |
Nr ziarna wg ASTM N | Średnia liczba
ziarn na 1 dm² przy
powiększeniu 100x
n =2r-1 | Średnia powierzchnia
poprzecznego
przekroju ziarna | Średnica przekroju kulistego ziania
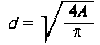
mm | Średnia liczba ziaren | Średnia ogólna powierzchnia |
przy pow. 100 x
A`=1/n
dm² | rzeczywisty
wymiar
A = 0,0645 A' mm² |
w 1 dm³
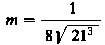 | w 1 mm³
| 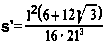
|
| |
-1 | 0,25 | 4 | 0,258 | 0,574 | 91 200 | 5,6 | 125 | 4,7 | |
0 | 0,5 | 2 | 0,129 | 0,406 | 261 000 | 15,9 | 170 | 6,7 | |
1 | 1 | 1 | 0,0645 | 0,287 | 739 000 | 45,1 | 240 | 9,5 | |
2 | 2 | 0,5 | 0,0323 | 0,203 | 2 090 000 | 128 | 340 | 13,4 | |
3 | 4 | 0.75 | 0,016 1 | 0,144 | 5 090 000 | 360 | 480 | 18,9 | |
4 | 8 | 0,125 | 0,008 06 | 0,101 | 16 700 000 | 1 020 | 679 | 26,7 | |
5 | 16 | 0,0625 | 0,00403 | 0,071 8 | 47 300 000 | 2 880 | 961 | 37,8 | |
6 | 32 | 0,031 3 | 0,002 02 | 0,050 7 | 134 000 000 | 8 160 | 1 360 | 53,4 | |
7 | 64 | 0,015 6 | 0,001 01 | 0,035 9 | 378 000 000 | 23 000 | 1 920 | 75,6 | |
8 | 128 | 0,078 | 0,000 504 | 0,025 4 | 1 070 000 000 | 65 300 | 2 720 | 107 | |
9 | 256 | 0,039 | 0,000 252 | 0,017 9 | 3 030 000 000 | 184 000 | 3 840 | 151 | |
10 | 512 | 0,0020 | 0,000126 | 0,012 7 | 8 560 000 000 | 522 000 | 5 430 | 214 | |
11 | 1024 | 0,0010 | 0,000 063 | 0,009 0 | 24 200 000 000 | 1 470 000 | 7 690 | 302
| |
|
Jeżeli istnieje steksturowanie, wtedy kula projekcji przestrzennej jest nierównomiernie pokryta punktami przebicia prostopadłych do płaszczyzn krystalograficznych. Refleksja wystąpi tylko tam, gdzie koło refleksji pokrywa się z obszarami odłożonymi na kuli projekcji przestrzennej. Nierównomierne zaczernienie linii rentgenowskich (prążków) jest tylko jakościowym wskaźnikiem istniejącego steksturowania.
Równomiernie zaczernione linie nie odznaczają jednak dowolnych orientacji krystalograficznych. Istnieją tekstury, w których pewne płaszczyzny pokrywają kulę projekcji przestrzennej równomiernie, a inne nierównomiernie. Oprócz tego należy zachować pewną ostrożność przy interpretacji linii Debye'a, dla których kąt ugięcia promieni wynosi około 90°, ponieważ koła refleksji takiej płaszczyzny obejmują tylko niewielką część kuli projekcji przestrzennej.
W celu całkowitego wyznaczenia tekstury warstwy wierzchniej należy całą powierzchnię kuli projekcji przestrzennej pokryć punktami przebicia prostopadłych do płaszczyzn krystalograficznych.
W niektórych przypadkach tworzenia się warstwy wierzchniej, np. przez walcowanie, można wyznaczyć steksturowanie za pomocą zdjęć obrotowych, jeśli niskosymetryczne kierunki płaszczyzn są zgodne z kierunkiem walcowania lub z kierunkiem prostopadłym do kierunku walcowania.
Dla obu kierunków wykonuje się zdjęcia obrotowe, wyznaczając z otrzymanych diagramów warstwicowych kierunek krystalitów równoległy do osi obrotu próbki. Ponieważ płaszczyzny krystalitów zachowują identyczne kierunki do powierzchni próbki, dlatego można ustalić położenie badanej płaszczyzny krystalograficznej.
W wielu przypadkach w ten sposób nie można wyznaczyć steksturowania warstwy wierzchniej, ponieważ wysokosymetryczne kierunki krystalograficzne nie zawsze są równoległe do uprzywilejowanego kierunku makronierówności (np. walcowanie). W takich przypadkach należy wykonać projekcję stereograficzną, za pomocą której przedstawia się płaszczyzny i kierunki krystalograficzne w przestrzeni. Z rzutu stereograficznego wybiera się rozkład tylko jednego rodzaju płaszczyzn sieciowych dla wielkiej liczby krystalitów badanej objętości i sporządza figury biegunowe.
Teksturę warstwy wierzchniej można wyznaczyć za pomocą goniometru teksturowego, dzięki czemu można zmniejszyć liczbę zdjęć rentgenowskich. Goniometr rentgenowski ma kamerę, w której są robione zdjęcia. W kamerze znajduje się obracana badana próbka i błona filmowa, które w czasie wykonywania zdjęć są ustawione w ten sposób, że każde położenie próbki jest podporządkowane określonej części zdjęcia.
Interpretacja błony filmowej jest taka sama, jak w przypadku zdjęć wykonywanych w innych kamerach.
Kamery goniometrów teksturowych są cylindryczne lub płaskie.
W goniometrze z płaską kamerą błonę filmową płaską ustawia się prostopadle do kierunku promienia wiązki pierwotnej przesuniętej wewnątrz w stosunku do promieniowego kierunku osi obrotu próbki. Przed błoną filmową znajduje się osłona z okrągłą szczeliną. Mechanizm kontaktowy powoduje zwrot kierunku obrotu próbki i ruch błony filmowej, po obrocie próbki o 90°.
Wielką zaletą goniometru z płaską kamerą jest to, że koło Debye'a, utworzone przy różnych kątach obrotu próbki, oraz leżąca na błonie filmowej siatka z dziesięciostopniowymi odstępami dzieli zaczernioną powierzchnię na obszary, które formą i odzwierciedleniem odpowiadają obszarom na figurach biegunowych. W ten sposób jest możliwe bezpośrednie przenoszenie obrazu rentgenowskiego do projekcji stereograficznej. W przypadku teksturowania warstwy wierzchniej stalowych elementów maszyn-płaszczyzna (110) układa się równolegle do powierzchni, a kierunek krystalograficzny (l 12) jest równoległy do kierunku działania siły odkształcającej warstwę. Na podstawie figur biegunowych wyznacza się orientacje krystalograficzne ziarn, czyli steksturowanie warstwy wierzchniej.
3.5.3.6. Metody badania wad materiału warstwy wierzchniej
Wady materiału warstwy wierzchniej powstają podczas wytopu, przeróbki plastycznej na gorąco, obróbki mechanicznej i cieplnej oraz obróbki powierzchniowej.
Występują w zasadzie dwa rodzaje wad materiału warstwy wierzchniej: wtrącenia niemetaliczne i pęknięcia.
Wtrącenia niemetaliczne wykrywa się najdokładniej za pomocą mikrosondy.
Pęknięcia metalu warstwy wierzchniej wykrywa się przez oględziny zewnętrzne, nasycanie naftą, metodą fluoroscencyjną, nasycanie olejem, metodą magnetyczną, metodą magnetyczno-akustyczną, metodą rentgenowską, metodą ultradźwiękową i metodą metalograficzną.
Oględziny zewnętrzne. Skuteczność tej metody można zwiększyć przez powlekanie badanej powierzchni olejem. Korodujący metal w szczelinach spowoduje zabarwienie oleju.
Nasycenie naftą. Badaną powierzchnię pokrywa się naftą na okres około jednej godziny. Po wyjęciu elementu z nafty i wytarciu powierzchni posypuje sieją np. kredą sproszkowaną. Lokalne plamy na warstewce kredy świadczą o istnieniu szczelinek w warstwie wierzchniej.
Metoda fluorescencyjna. Badany element maszyny zanurza się w zawiesinie preparatu fluoryzującego. Po wyjęciu obserwuje się w ciemni badaną powierzchnię. Nagromadzony preparat fluoryzujący w szczelinach umożliwia ich wykrycie.
Nasycenie olejem. Badany element maszyny zanurza się w rozgrzanym oleju i następnie po wyjęciu i wytarciu powierzchnię jego powleka się farbą wapienną. Tłuste plamy świadczą o istnieniu pęknięć.
Metody magnetyczne. W metodach magnetycznych wykorzystuje się wpływ wewnętrznych wad materiału na jego przenikalność magnetyczną. Metoda umożliwia badanie wad materiału wewnątrz warstwy wierzchniej. Pęknięcia powodują lokalne zmniejszenie przenikalności magnetycznej, wskutek czego linie pola magnetycznego ulegają ugięciu.
Metoda magnetyczno-akustyczna. Badany element maszyny umieszcza się w polu magnetycznym, a cewkę indukcyjną (czujnik) przemieszcza się wzdłuż badanej powierzchni. Zmiany składowej normalnej pola magnetycznego, spowodowane występowaniem pęknięć, wywołują w cewce indukcyjnej przepływ prądu, który po wzmocnieniu daje sygnał dźwiękowy.
Metoda rentgenowska (defektoskopia rentgenowska). Pewną odmianą metody rentgenowskiej jest stosowanie zamiast promieni rentgenowskich promieniowania gamma, emitowanego przez izotopy promieniotwórcze.
Metoda ultradźwiękowa. Metoda umożliwia wykrywanie nie tylko pęknięć, ale również wtrąceń niemetalicznych, pęcherzy i porowatości. Przy dyfraktoskopii ultradźwiękowej stosuje się fale sprężyste o częstotliwości 2 • 104 Hz do 3 • 109 Hz. Wykorzystuje się rozprzestrzenianie fal w ośrodkach stałych, załamanie i odbijanie na granicach ośrodków.
Badania metalograficzne. Badania te są przeprowadzane za pomocą mikroskopów optycznego i elektronowego na skośnych zgładach przekroju poprzecznego warstwy wierzchniej lub na powierzchni badanej. Badanie gradientu wad materiału warstwy wierzchniej jest prowadzone jedną z wymienionycli metod w zasadzie przy stopniowym strawieniu materiału warstwy wierzchniej.
Stan warstwy wierzchniej można określić wtedy, gdy mamy zmierzone wartości, gradienty i rozkłady poszczególnych jej parametrów.
|