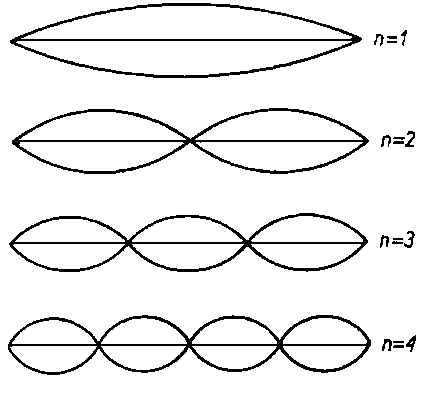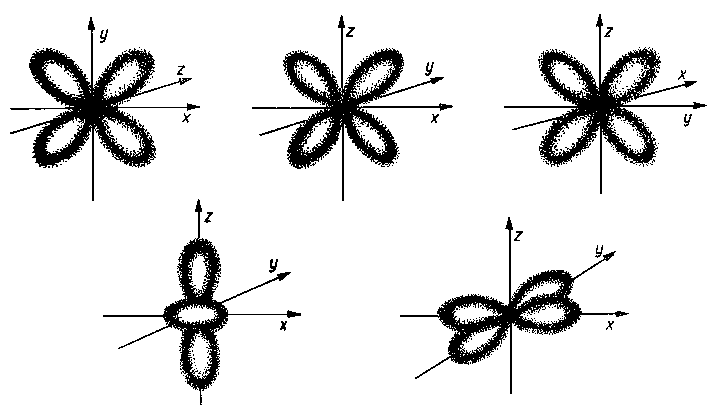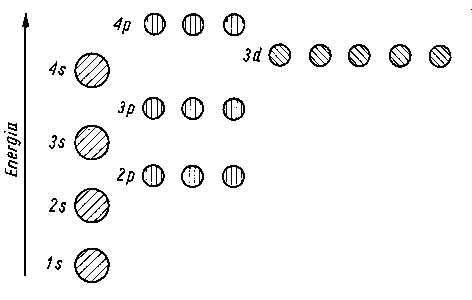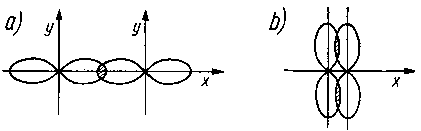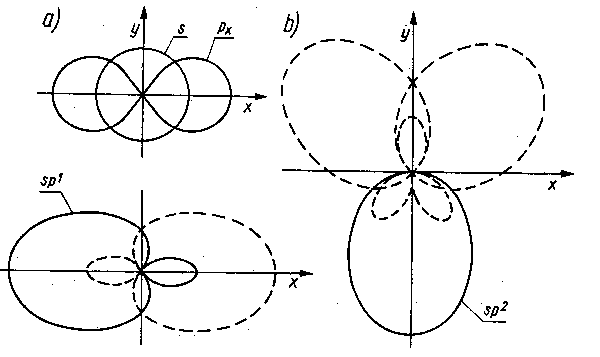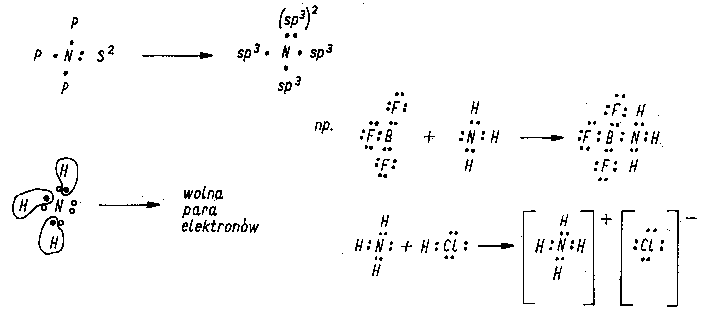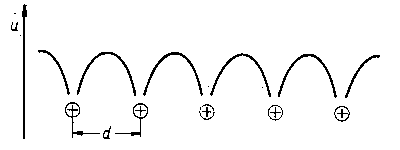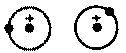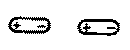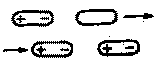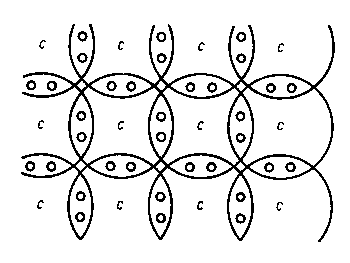| |
2. Podstawy procesów tarcia
2.1. Tarcie
Tarciem nazywamy zbiór zjawisk występujących w obszarze styku dwóch przemieszczających się względem siebie ciał, w wyniku których powstają opory ruchu.
Miarą tarcia jest opór równoważony wypadkową siłą styczną podczas przemieszczania jednego ciała względem drugiego. Przy przemieszczaniu względnym dwóch ciał występuje tarcie kinetyczne (ruchowe), przy czym jeśli prędkość względna obszarów tarcia dwóch ciał jest równa zeru, występuje wówczas tarcie statyczne (spoczynkowe).
Tarcie kinetyczne ze względu na rodzaj ruchu można podzielić na tarcie ślizgowe i tarcie toczne. Przy tarciu ślizgowym obszarem styku jest zazwyczaj powierzchnia płaska lub zakrzywiona. Wyróżniane przez niektórych autorów tarcie wiertne jest szczególnym rodzajem tarcia ślizgowego, przy którym obszarem styku jest przekrój kołowy równocześnie przemieszczający się osiowo. Przy tarciu tocznym obszarem styku elementów jest punkt (tarcie kuł) lub linia (tarcie ciał o kształtach cylindrycznych lub cylindrycznym i płaskim).
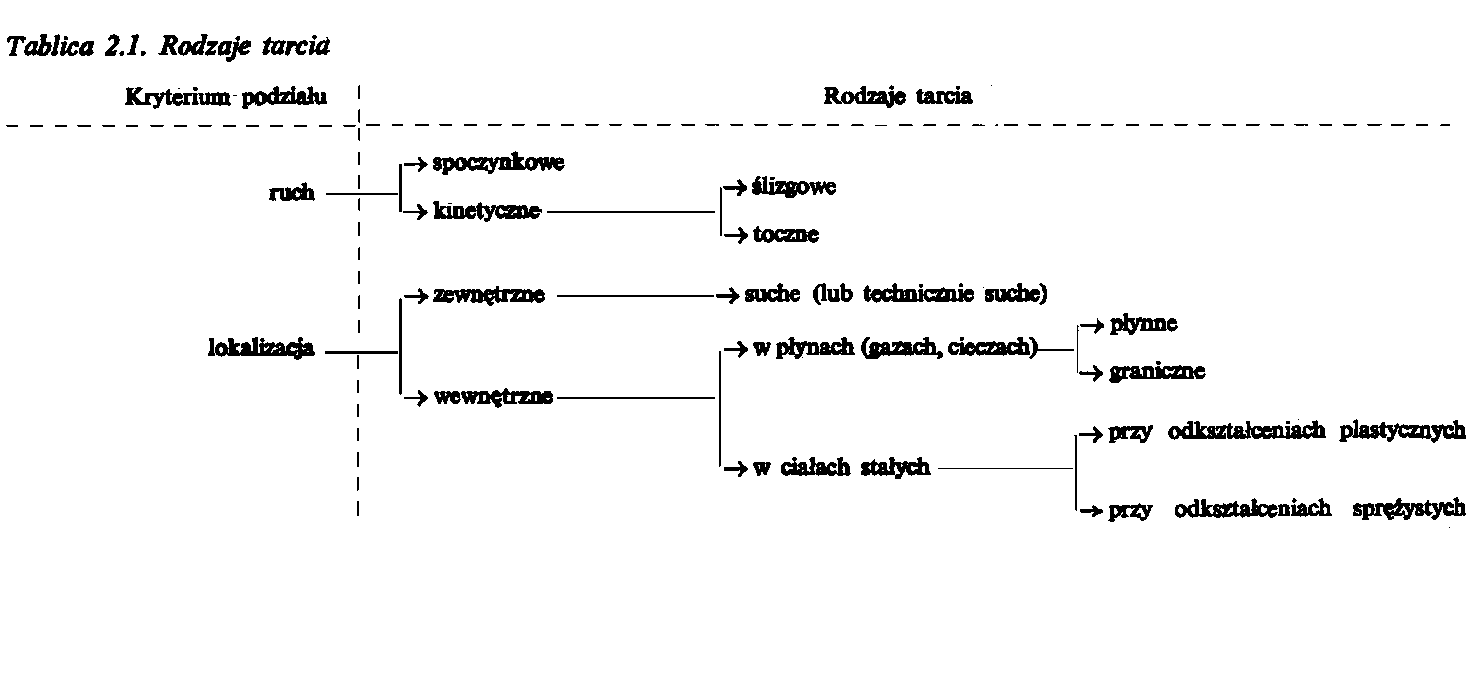
Tablica. 2.1. Rodzaje tarcia
 |
|
Tarcie może również występować w obrębie jednego ciała, gdy przemieszcza się względem siebie lub stara się wprowadzić w ruch poszczególne jego elementy składowe (np. warstwy, cząsteczki itp.). Ten rodzaj tarcia nazywa się tarciem wewnętrznym w przeciwieństwie do tarcia zewnętrznego występującego przy powierzchniowym styku ciał, np. w obszarach styku przemieszczających się względem siebie elementów maszyn.
Charakter tarcia wewnętrznego zależy od stanu skupienia ciała. W gazach ze względu na znaczne odległości między cząsteczkami istnieje duża swoboda wzajemnego przemieszczania, ponieważ opory tarcia są niewielkie. Rosną one wraz ze wzrostem intensywności ruchów termicznych cząstek. W cieczach odległości między cząsteczkami są znacznie mniejsze niż w gazach, wskutek tego swoboda przemieszczania jest mniejsza. Jeżeli warstwa lub warstwy cząsteczek cieczy znajdują się w zasięgu pola sił ciała stałego na granicy rozdziału faz ciecz-ciało stałe, wówczas swoboda przemieszczania tych cząsteczek zostaje znacznie ograniczona. Tarcie występujące w tych warstwach cieczy nazywa się tarciem granicznym. W ciałach stałych składowe elementy budowy (atomy, cząsteczki, jony) są rozmieszczane symetrycznie (zazwyczaj w siatce krystalicznej) i mają bardzo ograniczoną swobodę wzajemnego przemieszczania. Przemieszczanie takie występuje przy odkształceniach sprężystych i plastycznych. Mechanizm tych przemieszczeń jest zupełnie inny niż w cieczach, jednak w jednym i drugim przypadku siłami przeciwdziałającymi przemieszczaniu elementów są siły spójności (kohezji). Podział rodzajów tarcia przedstawiono w tabl. 2.1.
Z technicznego punktu widzenia najważniejszy jest podział tarcia na suche, graniczne i płynne. Dla zmniejszenia tarcia zewnętrznego staramy się rozdzielić powierzchnie trące warstwą substancji smarującej, czyli zastąpić tarcie suche ciał stałych tarciem płynnym, a więc tarciem wewnętrznym cieczy smarnej. Jeżeli ze względu na duże naciski jednostkowe warstwa cieczy podlega ,,wyciśnięciu" z przestrzeni między powierzchniami trącymi, pozostaje wówczas między nimi cieniutka warstewka cieczy utrzymująca się tam tylko wskutek wzajemnego oddziaływania cieczy z ciałami stałymi, zwana warstewką graniczną (filmem granicznym). Im silniejsze jest to wzajemne oddziaływanie, tym trwalsza jest ta graniczna warstewka. Zabezpiecza ona przed wystąpieniem tarcia suchego. Tarcie przy smarowaniu warstewkami granicznymi nazywa się tarciem granicznym.
W praktyce eksploatacyjnej maszyn dopuszcza się jedynie tarcie płynne i tarcie graniczne. Tarcie suche, oprócz przypadków, gdy jest ono pożądane (przekładnie cierne, hamulce itp.), jest z praktyki eksploatacyjnej eliminowane. Ze względu na to, że współpracujące powierzchnie nie są idealnie gładkie na wierzchołkach tych nierówności może występować tarcie suche lub graniczne, a we wgłębieniach tarcie płynne.
Rodzaj tarcia w makroobszarze jest wypadkową rodzajów tarcia występujących w mikroobszarach styku. W sumie tarcie w makroobszarze jest mieszaniną różnych rodzajów tarcia, a więc tarciem mieszanym. Tarcia mieszanego nie należy wyodrębniać jako osobnego rodzaju tarcia.
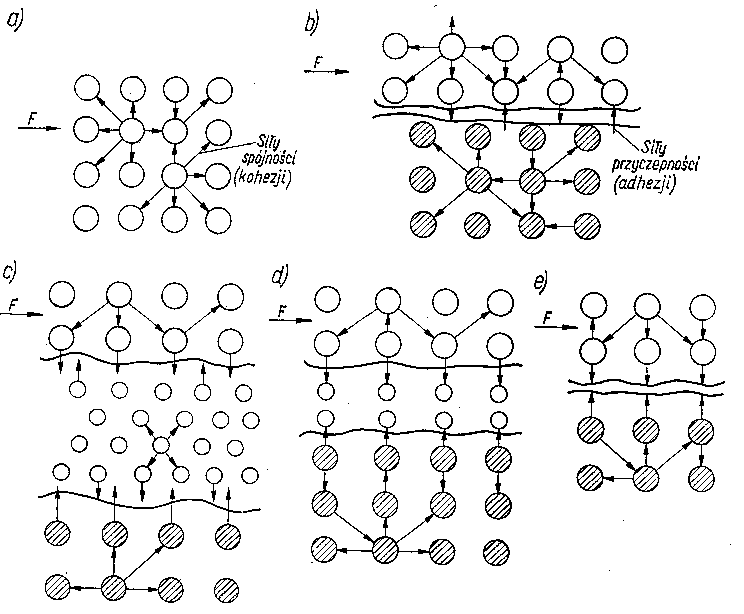 |
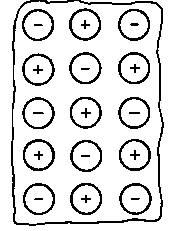
Rys. 2.1. Modele różnych rodzajów tarcia:
- tarcie wewnętrzne,
- tarcie zewnętrzne,
- tarcie płynne,
- tarcie graniczne,
- tarcie suche
|
Na rys. 2.1 przedstawiono różne rodzaje tarcia. Stykające się obszary tarcia ciał możemy przedstawić jako zbiory elementów budowy (atomów, cząsteczek, jonów) w kształcie kuł. Między tymi elementami działają siły, które je spajają w jedno ciało. Siły spajające zwane są siłami spójności lub siłami kohezji. Wyrywanie elementów budowy z kohezyjnego działania ich sąsiadów jest nazywane dekohezją (np. zużywaniem materiałów na skutek tarcia). Jak wynika z rys. 2.1 przy tarciu wewnętrznym opory są wywoływane oddziaływaniem sił kohezji. Przy tarciu zewnętrznym, gdy kontaktowane są ze sobą ciała o idealnych powierzchniach, występujące opory mają swoje źródło w oddziaływaniu sił powierzchniowych, czyli sil adhezji. Tak więc tarcie wewnętrzne jest wynikiem pokonywania sił spójności, a tarcia zewnętrzne - sił przyczepności.
Przy tarciu zewnętrznym rzeczywistych powierzchni następuje ścinanie nierówności, odkształcenie plastyczne, rysowanie itp. pokonywanie sił kohezji oraz sił adhezyjnych; na opory rzeczywistego tarcia zewnętrznego składa się zarówno człon adhezyjny, jak i człon kohezyjny.
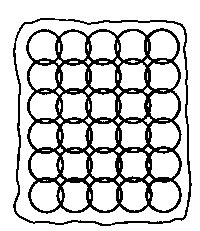
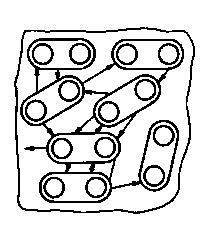
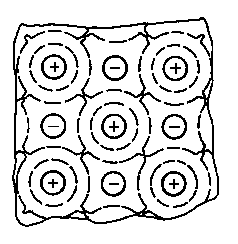
Jednym z podstawowych problemów trybologicznych jest zabezpieczenie współpracujących elementów maszyn przed zacieraniem. Osiąga się to poprzez wprowadzenie do substancji smarującej związków zwiększających intensywność jej wzajemnego oddziaływania z metalicznym podłożem (rys. 2.2).
Powyższe rozważania nasuwają wniosek, że zrozumienie procesów i zjawisk trybologicznych wiąże się ze znajomością budowy ciał i działających sił.
Procesy i zjawiska trybologiczne można rozpatrywać na różnych poziomach. Dla wyjaśnienia niektórych problemów konieczna jest analiza zjawisk występujących w obszarze jąder i elektronów. W innych przypadkach operujemy atomami i cząsteczkami lub też grupami cząsteczek, krystalitami itp. Dla niektórych celów zupełnie wystarcza analiza w makroobszarze (tabl. 2.2). Przy porównywaniu zjawisk trybologicznych można brać pod uwagę jedynie te same zakresy. Podstawą zjawisk towarzyszących tarciu ciał stałych i płynów jest ich budowa cząsteczkowa i wzajemne oddziaływanie.
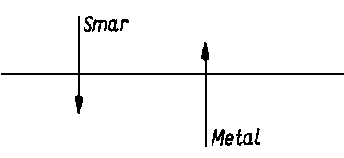 |
Rys. 2.2. Model oddziaływania substancji smarującej z metalem
|
|
Tablica 2.2. Obszary badań trybologicznych | |
Obiekt badań | Zakres badań | |
Jądra i elektrony | submolekularny | |
Atomy i cząsteczki | molekularny | |
Grupy cząsteczek krystality itd. | mikro | |
makro | Ciała, grupy ciał | |
2.2. Atomy i ich powłoki elektronowe
Teoria budowy materii pod koniec ubiegłego wieku nie była w pełni ugruntowana. Badania E. Rutheforda i współczesnych mu uczonych w pierwszym dziesiątku lat naszego stulecia udowodniły atomową budowę materii oraz pozwoliły stwierdzić, że atomy są złożone z dodatnio naładowanego jądra, zajmującego bardzo małą przestrzeń (promień r = 10 -13 do 10 -12 cm) i skupiającego prawie całą masę atomu oraz otaczających go w odległości do około 10 -8 cm (promień atomu) ujemnych elektronów o znikomo małej masie (masa mel = 0,9107 • 10 -27 g). W obojętnym atomie liczba elektronów jest równa liczbie porządkowej pierwiastka, a więc identyczna z liczbą ładunków jądra. Jądro atomowe składa się z nukleonów, tj. protonów i neutronów, których łączna liczba określa masę atomu (liczba masowa). Nukleony są związane w jądrze siłami jądrowymi. Liczba elementarnych ładunków w jądrze jest równa liczbie ujemnych ładunków elementarnych elektronów i jest ona numerem porządkowym (liczbą atomową w układzie okresowym pierwiastków. Pomiędzy jądrem a elektronami w atomie działają siły przyciągania elektrostatycznego utrzymujące cały układ jądra w równowadze. Własności chemiczne i większość własności fizycznych pierwiastków zależą wyłącznie od struktury powłok elektronowych atomu, a nie od budowy jąder i z tego względu budowa powłok elektronowych będzie omówiona w szerszym zakresie. Z danych doświadczalnych (np. widma atomowe, widma rentgenowskie) wynika, że w powłoce elektronowej atomu muszą istnieć różne stany elektronowe o ściśle określonych wartościach energii i że elektrony mogą zajmować w przestrzeni wokół jądra tylko pewne, a nie dowolne pozycje energetyczne.
W wyniku tego przy badaniu widm atomowych nie uzyskuje się widm ciągłych. Pierwszym modelem, który czynił zadość takiemu postulatowi był planetarny model atomu Nielsa Bohra. W modelu Bohr przez analogię do słonecznego układu planetarnego zakładał, że wokół jądra w różnej odległości od niego poruszają się elektrony po torach eliptycznych lub kołowych, przy czym każdy tor ruchu elektronu jest ściśle związany z jego stanem energetycznym.
Według praw klasycznej elektrodynamiki elektron poruszający się wokół jądra można uważać za oscylator elektryczny emitujący promieniowanie, wskutek czego maleje jego energia aż do chwili, kiedy spada na jądro. W celu ominięcia tej trudności Bohr założył, że tylko przeskok elektronu z jednej orbity na drugą jest związany z emisją lub absorpcją energii, a różnica energii DE między dwoma stanami energetycznymi (przed i po przeskoku elektronu) z częstością światła emitowanego lub absorbowanego są związane wzorem E = hn (gdzie h - stała Plancka 6,623 • 10 -34 Js, n - częstość promieniowania). Bohr przyjął stałe orbity elektronowe. Jego model atomu pozwolił na wytłumaczenie niektórych wielkości uzyskiwanych doświadczalnie (np. obliczanie serii widmowych dla atomu wodoru), nie tłumaczył jednak zjawisk występujących zwłaszcza w przypadku atomów wieloelektronowych, nie tłumaczył również tworzenia cząsteczek z atomów.
Przyjęcie dualistycznej korpuskulamo-falowej koncepcji budowy materii (prace de Broglie'a), opracowane przez Heisenberga - zasady mechaniki kwantowej (1925 r.) oraz przez Schrödingera-zasady mechaniki falowej (1926 r.) pozwoliło na wprowadzenie nowej koncepcji modelu atomu.
W myśl zasady nieoznaczoności Heisenberga niemożliwe jest równoczesne dokładne ustalenie prędkości i położenia elektronu. Dlatego też mechanika falowa posługuje się pojęciem prawdopodobieństwa znalezienia się elektronu w elemencie przestrzeni wokółjądrowej. Orbity elektronowe z modelem atomu Bohra zostały zastąpione pojęciem orbitali, które charakteryzują przestrzenny rozkład największego prawdopodobieństwa znalezienia się elektronu w jakimś miejscu przestrzeni. Prawdopodobieństwo to musi być zgodne z falową koncepcją budowy materii. Zrozumienie nieciągłości budowy powłoki elektronowej ułatwia analogia do drgań umocowanej na obu końcach struny, dla której możliwe są jedynie określone stany oscylacyjne o określonych długościach fali ln, częstościach i energiach. Ze względu na to, że amplitudy drgań na końcach struny muszą się równać zeru, możliwe są tylko takie drgania, dla których długości fal ln, są związane z długością struny równaniem
|
n ln = 2 l | (2.1) | |
gdzie: l - długość struny, n - wartości całkowite 1,2,3, ... |
Drgania podstawowe o częstości (n = 1) i wyższe drgania harmoniczne o częstości n razy większej (n = 2, 3, 4, ...) odznaczają się charakterystyczną liczbą strzałek i liczbą węzłów, przy czym liczba węzłów dla jednego drgania n-tego stopnia wynosi n-1 (rys. 2.3).
Fale elektronowe są bardziej złożone niż omówione tu drgania struny chociażby z tego względu, że są falami przestrzennymi, a więc trójwymiarowymi. Można sobie je wyobrazić jako mechaniczne wzbudzone drgania chmury pyłu o kształcie kulistym, dla których węzły z drgania struny zostały zastąpione przez powierzchnie węzłowe.
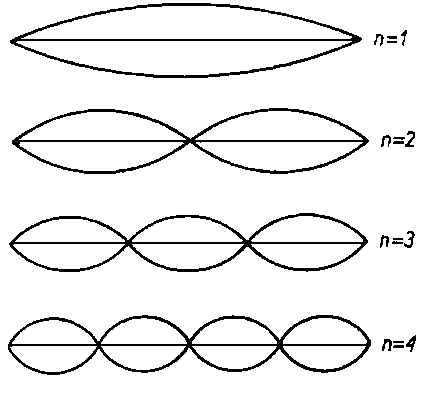 |
Rys. 2.3. Fale stojące w naprężonej strunie
|
Dla najprostszego modelu atomu, a więc atomu składającego się z protonu i elektronu, Schrödinger (w r. 1926) podał różniczkowe równanie falowe
| |
|
¶2 y
¶x2 | + |
¶2 y
¶y2 | + |
¶2 y
¶z2 | + |
8 p2 m
h2 | (E - U) y = 0
| (2.2)
|
|
Równanie to opisuje zależność pomiędzy całkowitą energią elektronu E, jego energią potencjalną U oraz funkcją falową Schrödingera y opisującą stan elektronu, a więc jego amplitudę w dowolnym punkcie przestrzeni o współrzędnych x, y, z (m = masa elektronu, h = stała Plancka). Wartość funkcji falowej Schrödingera określa prawdopodobieństwo znalezienia się elektronu w danym punkcie, czyli jest miarą gęstości elektronowej w danym punkcie i czasie.
Scałkowanie równania Schrödingera ma sens fizyczny tylko dla pewnych określonych wartości całkowitej energii elektronu. Tak więc wprost z matematycznego warunku całkowalności wynika kwantowanie energii elektronu.
Funkcja falowa opisująca najuboższy energetycznie stan elektronu ma przestrzennie symetryczny rozkład i ma postać skorupy sferycznej. Nie ma więc ona powierzchni węzłowych. Przy wyższych energetycznie stanach elektronowych funkcja falowa ma płaszczyzny węzłowe przechodzące przez środek atomu. Rozkład gęstości elektronowej ma w przestrzeni uprzywilejowane kierunki odpowiednio położone względem osi x, y, z.
Dla najuboższej energetycznie głównej liczby kwantowej n = 1 rozkład przestrzenny funkcji falowej, a więc rozkład prawdopodobieństwa znalezienia się elektronu w danym obszarze, czyli kształt orbitalu, przybiera postać skorupy sferycznej (rys. 2.4a). Dla liczby kwantowej n = 2 występuje już powierzchnia węzłowa przechodząca przez środek atomu, przy czym sam rozkład funkcji ma kształt przestrzennej ósemki (rys. 2.4b). Ósemka przestrzenna może być różnie usytuowana względem osi x, y, z, przy czym poszczególne warianty są pod względem energetycznym równocenne.
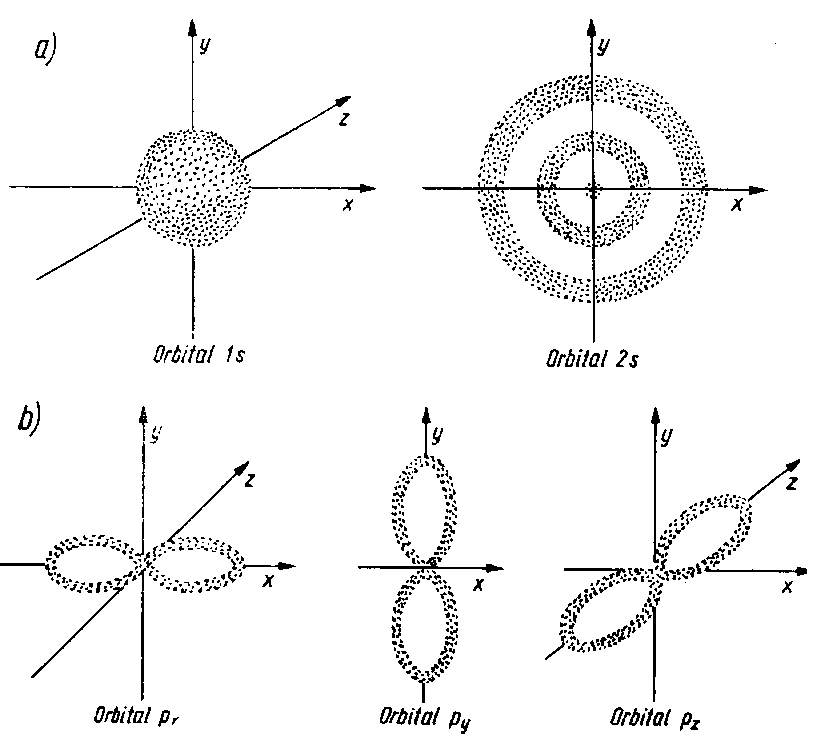 | |
Rys. 2.4. Kształt: a) orbitali s, b) orbitali p
|
Symetrię przestrzennego rozkładu gęstości elektronowej oraz liczbę przechodzących przez środek atomu powierzchni węzłowych określa poboczna liczba kwantowa l. Przy sferycznie symetrycznym rozkładzie ładunku poboczna liczba kwantowa l = 0, dla sferycznej ósemki l = 1, a dla sferycznej rozety l =2. Między główną liczbą kwantową n i poboczną liczbą kwantową l istnieje zależność:
0 ≤ l ≤ (n - 1)
Elektrony mające tę samą główną liczbę kwantową n należą do tej samej powłoki elektronowej. Poszczególne powłoki elektronowe oznacza się kolejno liczbami arabskimi lub literami alfabetu łacińskiego:
- dla głównej liczby kwantowej n = 1, 2, 3, 4, 5, 6, 7,
- liczbowy symbol powłoki elektronowej l, 2, 3, 4, 5, 6, 7,
- literowy symbol powłoki elektronowej K, L, M, N, O, P, Q.
Elektrony mające tę samą poboczną liczbę kwantową l w zakresie danej głównej liczby kwantowej n należą do tej samej podpowłoki elektronowej. Poszczególne podpowłoki elektronowe, oznacza się następującymi symbolami literowymi :
- poboczna liczba kwantowa l = 0, l, 2, 3,
symbol podpowłoki elektronowej s, p, d, f,
Symbole te zostały zaczerpnięte ze spektroskopii, gdzie określano nimi poszczególne serie spektralne:
s - seria ostra (sharp),
p - seria główna (principal),
d - seria rozmyta (diffuse),
f - seria podstawowa (fundamental).
Ze względu na rozmieszczenie elektronów w atomie należy więc wyróżnić powłoki elektronowe, które rozdzielają się na podpowłoki i orbitale.
Liczba podpowłok jest taka sama, jak liczba oznaczająca daną powłokę (czyli powłoka K ma jedną podpowłokę, powłoka L - dwie podpowłoki itd.).
Podpowłoki dzieli się na mniejsze jednostki zwane orbitalami. Liczba orbitali na danej powłoce wynosi tyle, ile wynosi kwadrat liczby określającej daną powłokę. Tak więc powłoka K ma l orbital, powłoka L ma 4 orbitale rozmieszczone na dwóch podpowłokach, powłoka M ma 9 orbitali rozmieszczonych na trzech podpowłokach. Rozmieszczenie orbitali na podpowłokach jest następujące:
- pierwsza podpowłoka każdej powłoki (najbliższa jądra) zawiera jeden orbital oznaczony s,
- druga podpowłoka (począwszy od drugiej powłoki) zawiera 3 orbitale nazywane orbitalami p,
- trzecia podpowłoka zawiera 5 orbitali zwanych orbitalami d,
- czwarta podpowłoka zawiera 7 orbitali zwanych orbitalami f.
Przynależność orbitali do danej powłoki i podpowłoki określa się liczbą oznaczającą powłokę oraz literą oznaczającą podpowłokę. Tak np. orbital 3s jest pojedynczym orbitalem s znajdującym się na pierwszej podpowłoce powłoki
trzeciej.
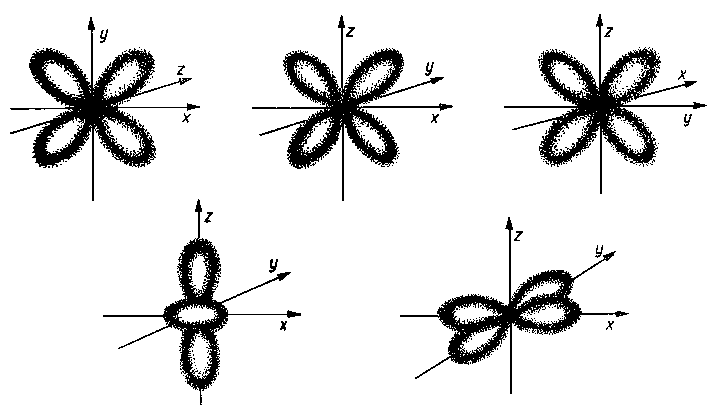 |
Rys. 2.5.
Kształt orbitali d
|
Kształt poszczególnych orbitali, czyli obszarów największego prawdopodobieństwa znalezienia się elektronu przedstawiają rys. 2.4 i 2.5.
Elektron poruszający się na orbitalu ma określony moment pędu. Moment ten jest skwantowany mechanicznie. Ruch elektronu powoduje powstanie pola magnetycznego, którego bieguny są rozmieszczane na osi prostopadłej do płaszczyzny ruchu elektronu (rys. 2.6).
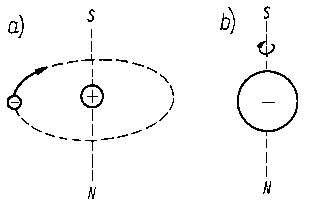 |
Rys. 2.6. Moment magnetyczny elektronu:
a) orbitalny,
b) spinowy
|
Moment magnetyczny M jest iloczynem masy magnetycznej bieguna i odległości między biegunami.
Moment magnetyczny powstający na skutek orbitalnego ruchu elektronów jest nazywany magnetycznym momentem orbitalnym . Jest on proporcjonalny do mechanicznego momentu pędu elektronu. Dla orbitali s jest on równy zeru, natomiast dla orbitali o wyróżnionym przestrzennie kierunku gęstości elektronowej (a więc p, d, f ) występują orbitalne momenty magnetyczne zależne od pobocznej liczby kwantowej l . W przypadku przyłożenia zewnętrznego pola magnetycznego następuje orientacja względem kierunku pola. Dla rozróżnienia możliwości orientacji momentów orbitalnych względem kierunku pola zewnętrznego służy trzecia liczba kwantowa zwana magnetyczną liczbą kwantową m . Orbitale o pobocznej liczbie kwantowej l mają kwantowe liczby magnetyczne m równe liczbom całkowitym od - l do +1. Dla orbitali p magnetyczne liczby kwantowe wynoszą -1, 0, + l. Dla pięciu orbitali d wynoszą one -2, -1, 0, +1, +2.
Poruszający się elektron jest elementarnym ładunkiem elektrycznym oraz elementarnym momentem magnetycznym. Dodatkową wielkością charakteryzującą różnice między stanami energetycznymi elektronów wynikające z ich ruchu obrotowego dokoła własnej osi (tzw. spinu lub krętu ) jest tak zwana kwantowa liczba spinowa s , która może przybierać dwie wartości s = +½ i s = -½. Ruch elektronu dokoła własnej osi powoduje powstanie momentu magnetycznego zwanego magnetycznym momentem spinowym (rys. 2.6).
Stan energetyczny elektronu w atomie charakteryzuje zespół czterech liczb kwantowych n, l, m, s . Według zakazu Pauliego nie mogą w atomie występować dwa elektrony o takim samym zespole liczb kwantowych. Tak więc między elektronem a resztą atomu działają przede wszystkim siły elektrostatyczne z pewnym niewielkim udziałem sił magnetycznych wynikających z magnetycznych momentów orbitalnych i spinowych.
Magnetyczne momenty orbitalne bardzo często redukują się przy odpowiednim usytuowaniu przestrzennym orbitali elektronowych. Podobnie redukują się magnetyczne momenty spinowe, gdy na tym samym orbitalu znajdują się dwa elektrony o przeciwnych spinach.
Oddziaływanie elektrostatyczne między jądrem a elektronami maleje dla elektronów znajdujących się na powłokach oddalonych od jądra wskutek wzrostu odległości, jak też wskutek ekranowania pola elektrostatycznego wytworzonego przez jądro powłokami elektronów leżących bliżej jądra. Z tego względu elektrony dalszych powłok są słabiej związane z atomami niż elektrony powłok znajdujących się w pobliżu jądra.
Przypatrując się budowie powłok elektronowych pierwiastków uszeregowanych w układzie okresowym stwierdzamy, że wraz ze wzrostem liczby atomowej pierwiastka wzrasta stopień zapełnienia powłok, podpowłok i orbitali (tabl. 2.3). Na jednym orbitalu mogą znajdować się maksymalnie dwa elektrony, przy czym muszą one mieć przeciwnie skierowane spinowe momenty magnetyczne (zasada Pauliego).
|
Tablica 2.3. Modele konfiguracji elektronowej pierwiastków (od wodoru do tytanu) | |
Powłoka | 1 | 2 | 3 | 4 | |
Podpowłoka | 1 | 1 | 2 | 1 | 2 | 3 | 1 | | |
Orbital | 1 | 2 | 2px | 2py | 2pz | 3 | 3px | 3py | 3pz | 3d/pięć orbitali | 4s | | |
H | 1 | | | | | | | | | | | | |
He | 2 | | | | | | | | | | | | |
Li | 2 | 1 | | | | | | | | | | | |
Be | 2 | 2 | | | | | | | | | | | |
B | 2 | 2 | 1 | | | | | | | | | | |
C | 2 | 2 | 1 | 1 | | | | | | | | | |
N | 2 | 2 | 1 | 1 | 1 | | | | | | | | |
O | 2 | 2 | 2 | 1 | 1 | | | | | | | | |
F | 2 | 2 | 2 | 2 | 1 | | | | | | | | |
Ne | 2 | 2 | 2 | 2 | 2 | | | | | | | | |
Na | 2 | 2 | 2 | 2 | 2 | 1 | | | | | | | |
Mg | 2 | 2 | 2 | 2 | 2 | 2 | | | | | | | |
Al | 2 | 2 | 2 | 2 | 2 | 2 | 1 | | | | | | |
Si | 2 | 2 | 2 | 2 | 2 | 2 | 1 | 1 | | | | | |
P | 2 | 2 | 2 | 2 | 2 | 2 | 1 | 1 | 1 | | | | |
S | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 1 | 1 | | | | |
Cl | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 1 | | | | |
A | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | | | | |
K | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 0 | 1 | | |
Ca | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 0 | 2 | | |
Sc | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 1 | 2 | | |
Ti | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | |
|
W przypadku mniejszych atomów dany orbital zapełnia się elektronami dopiero wówczas, gdy wszystkie orbitale bliższe jądra (czyli o niższej energii) zostały już zapełnione (rys. 2.7).
Podczas zapełniania elektronami orbitali p na każdym z trzech orbitali p pojawia się najpierw po jednym elektronie, zanim któryś z orbitali p będzie obsadzony przez dwa elektrony. Jest to tzw. reguła Hunda, którą stosuje się również do orbitali d i f Rys. 1.1.
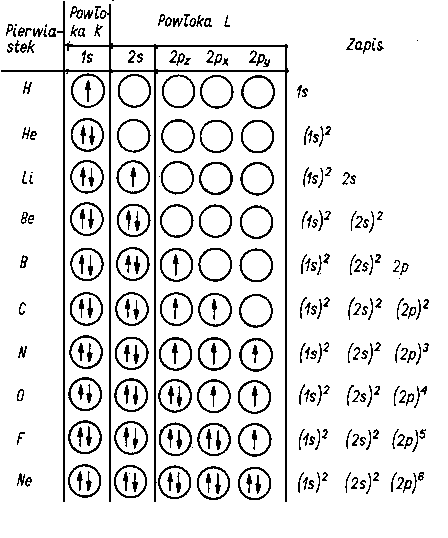 |
Rys. 2.7. Model zapełniania powłok przez elektrony
|
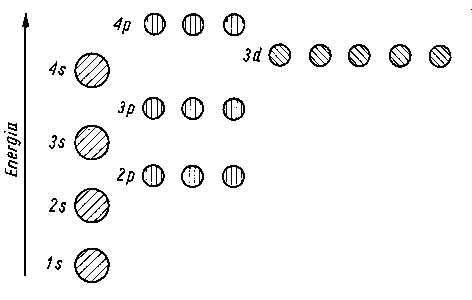 |
Rys. 2.8. Kolejność obsadzania orbitali przez elektrony
|
Jak widać z rys. 2.8 orbital 4s zapełnia się przed orbitalem 3d, gdyż ma od niego niższą energię elektronu. Względami energetycznymi można wyjaśnić i inne przypadki zastosowania reguły Hunda. Energia wzajemnego odpychania się dwóch elektronów, które mają zająć dwa wolne orbitale o tej samej energii (tzw. orbitale zdegenerowane) jest mniejsza, jeżeli elektrony te mają spiny niesparowane. Nie mogą więc one jednocześnie zajmować tego samego orbitalu.
W układzie okresowym pierwiastków powłoki zostają rozbudowane w ten sposób, że przy przejściu do kolejnego pierwiastka jest zajmowany zawsze poziom najuboższy energetycznie.
2.3. Wiązania między atomami
2.3.1. Wiązanie kowalencyjne
Atomy pierwiastków mogą się ze sobą łączyć w cząsteczki tego samego lub różnych pierwiastków. Jeżeli cząsteczka składa się z atomów różnych pierwiastków, to mamy do czynienia ze związkiem chemicznym. Atomy w cząsteczce mogą być związane różnego rodzaju wiązaniami. Jednym z podstawowych rodzajów wiązań jest wiązanie kowalencyjne (homeopolarne). Polega ono na uwspólnieniu elektronów pochodzących (po jednym) z obu łączonych atomów i utworzeniu pomiędzy atomami jednej, dwóch lub trzech par elektronów wiążących. Parą elektronów wiążących nazywamy taką parę elektronów, która ma wspólny dla obu atomów orbital. Orbital ten, ponieważ należy w równym stopniu do obu atomów tworzących cząsteczkę, nazywa się orbitalem cząsteczkowym (molekularnym). Do jego utworzenia dochodzi w ten sposób, że przy zbliżaniu do siebie dwóch atomów, elektron należący do jednego z atomów, dostaje się w zasięg działania pola elektrostatycznego jądra drugiego atomu. W ten sposób jest niemożliwe przyporządkowanie danego elektronu określonemu jądru atomowemu. Obydwa jądra atomowe zostają jakby „zanurzone" w jednej wspólnej chmurze elektronowej obu elektronów. Powstający w ten sposób wiążący orbital cząsteczkowy jest zajęty przez dwa elektrony o przeciwnym spinie (obracają się one wokół swych osi w przeciwnych kierunkach). W tworzeniu orbitali cząsteczkowych mogą brać udział orbitale powłok zewnętrznych, gdyż wnikaniu do głębszych powłok przy zbliżaniu się atomów do siebie przeciwdziałają siły odpychania.
Wiązanie kowalencyjne, a więc orbital cząsteczkowy może powstać wtedy, gdy tworzące go orbitale atomowe nie różnią się od siebie znacznie energią. Z tego względu przy tworzeniu wiązania kowalencyjnego mogą uczestniczyć zazwyczaj tylko orbitale należące do tej samej powłoki, gdyż różnią się one mało energią.
Każdy atom dąży do wykorzystania wszystkich orbitali powłoki zewnętrznej w tworzeniu wiązania. Wskutek tego na powłoce 2 w tworzeniu wiązania w równym stopniu może uczestniczyć jeden orbital 2s jak i trzy orbitale 2p.
Powstanie orbitali cząsteczkowych z orbitali s oraz orbitali p przedstawiono na rys. 2.9 i 2.10.
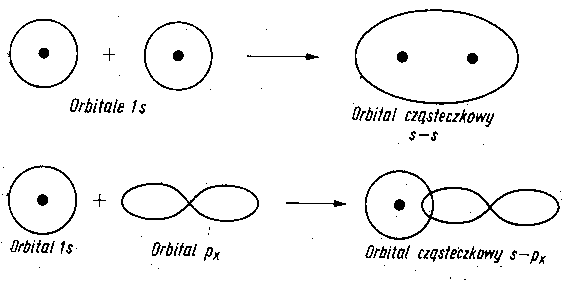 |
Rys. 2.9. Tworzenie orbitali cząsteczkowych
|
Jeżeli orbital cząsteczkowy wykazuje symetrię obrotową w stosunku do linii łączącej jądra obu połączonych atomów, wówczas utworzone wiązanie kowalencyjne jest nazywane wiązaniem (przenikaniem) typu s (rys. 2. l la), natomiast gdy utworzony orbital jest prostopadły do linii łączącej oba jądra, wówczas taki orbital jest nazywany wiązaniem typu p (rys. 2.11b).
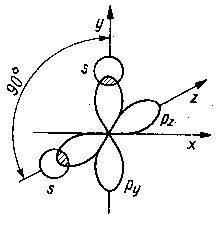
Rys. 2.10. Przenikanie orbitali s atomów wodoru z
orbitalami py, pz innego atomu |
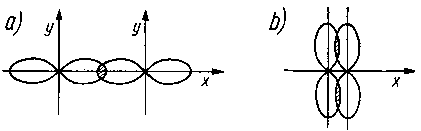
Rys. 2.11. Schemat przenikania orbitali p:
a) typu s,
b) typu p
|
Przy tworzeniu orbitalu cząsteczkowego wydziela się energia. Utworzony orbital, czyli utworzone wiązanie kowalencyjne, jest tym trwalsze, im więcej energii wydzieli się, a więc im niższy będzie stan energetyczny nowego układu. Minimum energii układu zostaje osiągnięte wówczas, gdy orbitale elektronów wiążących nakładają się w maksymalnym stopniu. Obowiązuje tu zasada maksymalnego pokrywania się orbitali. Ze względu na to, że poszczególne orbitale atomowe są w określony sposób rozłożone przestrzennie, maksymalne pokrywanie się orbitali przy tworzeniu orbitalu cząsteczkowego może być zrealizowane jedynie wówczas, gdy tworzący się orbital cząsteczkowy będzie ukierunkowany przestrzennie. To ukierunkowanie przestrzenne jest jedną z podstawowych cech wiązania kowalencyjnego. Pauling w swoich rozważaniach nad istotą wiązań chemicznych stwierdził, że jeżeli w powłoce zewnętrznej atomu jest kilka orbitali, to efekt lepszego pokrywania się przy tworzeniu orbitali cząsteczkowych może być osiągnięty wówczas, gdy orbitale atomowe atomu wchodzącego w reakcję nałożą się na siebie i wytworzą nowe orbitale równocenne energetycznie. Taki proces jest nazywany hybrydyzacją orbitali. Tak więc hybrydyzacją jest to przekształcenie dwóch lub więcej orbitali tej samej powłoki, lecz różnych podpowłok w nowe orbitale o tej samej energii.
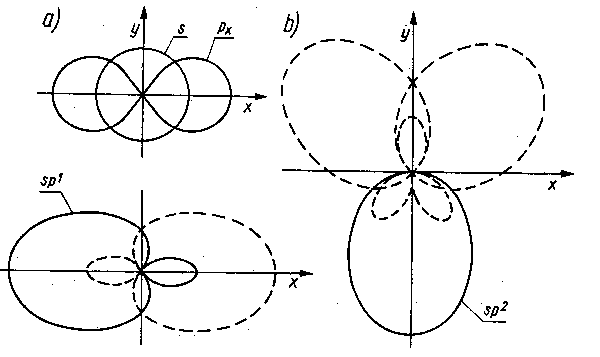 |
Rys. 2.12. Hybrydyzacja orbitali:
a) hybryd powstały z orbitali s i px,
b) hybryd powstały z orbitali s, px i py
|
Jeżeli hybrydyzacji ulegają orbitale: jeden 2s i jeden 2p, to nowy orbital jest nazywany orbitalem sp (rys. 2.12a). Gdy przekształceniu ulegają orbitale: jeden 2s i dwa 2p to nowy orbital nazywa się orbitalem sp2 (rys. 2.12b). Jeżeli przekształceniu ulegają wszystkie trzy orbitale 2p wraz z orbitalem 2s, to nowy orbital jest nazywany wówczas orbitalem sp3.
Hybrydyzację można przykładowo rozpatrzyć dla atomu pierwiastka węgla. Ma on następującą konfigurację elektronową:
|
orbital | 1s | 2s | 2px | 2py | 2pz | |
liczba elektronów | 2 | 2 | 1 | 1 | 0 |
Ponieważ orbital 2s ma dwa elektrony, a orbital 2pz< nie ma ich wcale, dlatego pełne wykorzystanie czterech orbitali na wytworzenie wiązań wymaga promowania jednego z elektronów z orbitalu 2s na wolny orbital 2pz, co powoduje, że na każdym z czterech orbitali powłoki 2 znajduje się jeden elektron. Hybrydyzacją tych orbitali (sp3) daje cztery orbitale o jednakowej energii, skierowane w stronę naroży czworościanu równoległego. Kąty między nimi wynoszą 109° (rys. 2.13).
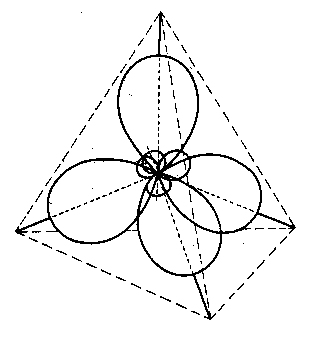 |
Rys. 2.13. Kształt i rozprzestrzenianie „chmur ładunków” czterowiązalnego atomu węgla przy tetraedrycznej hybrydyzacji s p3
|
Fakt ten stanowi teoretyczne kwantowo-mechaniczne wyjaśnienie tetraedrycznej konfiguracji atomu węgla, dawno już poznanej empirycznie.
Każdy z czterech orbitali s p3 zawiera jeden elektron i może być zapełniony w wyniku nałożenia na orbital z jednym elektronem o przeciwnym spinie innego atomu.
W ten sposób jeden elektron orbitalu l s atomu wodoru może nałożyć się na jeden z orbitali s p3, tworząc nowy orbital cząsteczkowy. Jest to orbital cząsteczkowy typu s, gdyż jest on symetryczny względem linii łączącej jądra atomu węgla i wodoru. Oznacza się go jako orbital cząsteczkowy s-s p3. Jeżeli w ten sposób w tworzeniu wiązań z atomem węgla wezmą udział cztery atomy wodoru, to zostaną zapełnione wszystkie orbitale i utworzy się związek CH4.
Do wyjaśnienia pozostaje jeszcze kształt orbitali zhybrydyzowanych. Jak widać z rys. 2.12 i 2.13 orbitale te po jednej stronie płaszczyzny węzłowej mają postać silnie skurczonych elipsoid obrotowych, po drugiej zaś silnie rozdętych. Wynika to z tego, że orbital p jest przedzielony płaszczyzną węzłową na dwie części, w których funkcja falowa Schrödingera ma odmienny znak. Jeżeli taki orbital zhybrydyzuje się z orbitalem s, który wobec braku płaszczyzny węzłowej ma zawsze wartość dodatnią, wtedy w wyniku sumowania po jednej stronie płaszczyzny węzłowej wartości funkcji falowej będą się dodawać (rozdęcie), a po drugiej odejmować (skurczenie).
Opierając się na zasadach mechaniki kwantowej można wytłumaczyć również budowę cząsteczek związków aromatycznych, np. cząsteczki benzenu. W sześciowęglowej cząsteczce benzenu przyjmowano dotychczas, że wchodzące w jej skład atomy węgla są wiązane na przemian wiązaniami pojedynczymi i podwójnymi, pomimo że eksperymentalnie ustalono równocenność wszystkich wiązań w cząsteczce. Według teorii kwantowo-mechanicznej atomy węgla w cząsteczce powiązane są ze sobą wiązaniami typu s, a dodatkowo wiązaniami typu p (rys. 2.14).
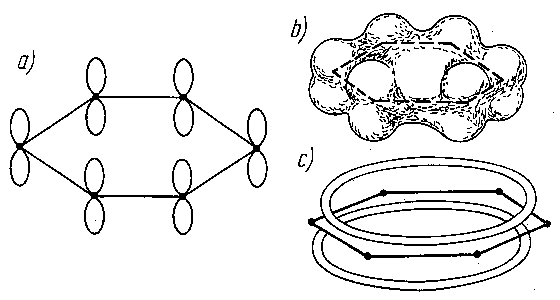 |
Rys. 2.14. Zlewanie się orbitali p w cząsteczce benzenu:
a) schemat sześciowęglowej cząsteczki benzenu,
b) wspólna chmura elektronowa atomów węgla w cząsteczce benzenu,
c) schemat tej chmury
|
Prawdopodobieństwo przenikania orbitali s z lewym i prawym sąsiadem jest zupełnie identyczne. Dlatego też jest niemożliwe łączenie określonych elektronów p w pary z utworzeniem wiązań p, jak też niemożliwa jest ich lokalizacja w określonych miejscach cząsteczki. Wszystkie wiązania między atomami węgla w pierścieniu aromatycznym muszą zawierać równy udział wiązania p, a rozkład gęstości ładunku elektronów p musi mieć wszędzie taką samą wartość (zlewanie się orbitali). W ten sposób znajduje wytłumaczenie symetria heksagonalna cząsteczki, wynikająca z równocenności wszystkich wiązań między atomami węgla. Wiązania między tymi atomami w benzenie nie są więc ani prostymi wiązaniami, ani formalnymi wiązaniami podwójnymi, lecz wykazują własności pośrednie między tymi dwoma typami wiązań. Powyższe wyjaśnienie pozwala zrozumieć charakter wiązań kowalencyjnych w związkach aromatycznych.
W podsumowaniu należy jeszcze raz podkreślić, że główną cechą wiązania kowalencyjnego jest uwspólnienie elektronów oraz ścisłe ukierunkowanie przestrzenne.
2.3.2. Wiązanie jonowe
Wiązanie jonowe zwane również wiązaniem heteropolarnym (różnobiegunowym), biegunowym lub elektrowalencyjnym jest wiązaniem bezkierunkowym, w którym występuje przyciąganie elektrostatyczne pomiędzy jonami wytworzonymi w wyniku całkowitego przejścia elektronów walencyjnych od atomu mniej elektroujemnego do atomu bardziej-elektroujemnego. W wyniku przejścia elektronu pierwszy atom staje się jonem dodatnim (kationem), drugi zaś jonem ujemnym (anionem); jony te w stanie stałym (krystalicznym) tworzą sieć jonową. Powstanie wiązania jonowego jest uwarunkowane wielkością energii jonizacji pierwiastka oddającego elektron, wartością powinowactwa elektronowego pierwiastka pobierającego elektron oraz wartością energii tworzącej się sieci krystalicznej.
Energia jonizacji, określana również jako potencjał jonizacyjny, jest to energia potrzebna do oderwania z pojedynczego atomu najluźniej związanego elektronu. Rozróżnia się energię jonizacji pierwszego, drugiego i dalszych elektronów. Energia jonizacji jest wyrażona zazwyczaj w elektronowoltach (l eV = 1,60210 • 10 -16 J). Wartość energii jonizacji zależy między innymi od wartości promienia atomu. Im mniejszy jest promień atomu, tym elektrony powłoki zewnętrznej leżą bliżej jądra, a więc są przez jądro silniej przyciągane i dlatego trudniej je oderwać. Najłatwiej oderwać elektrony walencyjne, czyli elektrony powłoki zewnętrznej, od atomów tych pierwiastków, które mają ich niewiele. Najwyższe wartości energii jonizacji mają pierwiastki, których atomy mają osiem elektronów walencyjnych (s2p6), a więc gazy szlachetne.
Pierwiastkom leżącym po lewej stronie układu okresowego odpowiadają małe wartości potencjału jonizacji, natomiast pierwiastki leżące z prawej strony mają duże potencjały jonizujące.
Drugim czynnikiem warunkującym powstanie wiązania jonowego jest elektroujemność pierwiastka pobierającego elektron. Przez elektroujemność rozumie się skłonność atomów do przyłączania elektronów, natomiast energia, która się uwalnia przy przyłączeniu elektronu do elektrycznie obojętnego atomu, nazywa się powinowactwem elektronowym. Największe powinowactwo elektronowe mają pierwiastki, których atomy mają zewnętrzne powłoki elektronowe niemal całkowicie zapełnione i przez pobranie elektronu uzupełniają swoją powłokę upodobniając się do powłok gazu szlachetnego.
Atomy mające niewielką liczbę elektronów na zewnętrznej powłoce łatwiej je oddają niż przyjmują. Związanie przyjętego elektronu jest tym silniejsze, im mniejszy jest promień atomu, gdyż wtedy elektron znajduje się blisko jądra i działają na niego duże siły przyciągania.
Elektroujemność jest zazwyczaj wyrażona w jednostkach porównawczych. Istnieje kilka skal porównawczych elektroujemności. Największe zastosowanie znajduje skala Paulinga (tabl. 2.4). Jak wynika z danych w tablicy w poszczególnych okresach elektroujemność jest tym większa, im więcej elektronów zawiera warstwa zewnętrzna. Dlatego też pierwiastki znajdujące się po lewej stronie układu okresowego mają małą elektroujemność.
|
Tablica 2.4. Wartości elektroujemności (wg Paulinga) dla kilku ważniejszych pierwiastków (dla H wynosi 2,1) | |
I | II | III | IV | V | VI | VII |
Li
1,0 | Be
1,5 | B
2,0 | C
2,5 | N
3,0 | O
3,5 | F
4,0 |
Na
2,9 | Mg
1,2 | Al
1,5 | Si
1,8 | P
2,1 | S
2,5 | Cl
3,0 |
K
0,8 | Ca
1,0 | | Ge
1,7 | As
2,0 | Se
2,4 | Br
2,8 |
Rb
0,8 | | | Sn
1,7 | | | J
2,4
|
|
Tablica 2.5. Zależności między wartościami elektroujemności A a charakterem jonowym wiązań pojedynczych B
|
|
A | B | |
1,0 | 19,5 | |
1,2 | 24 | |
1,4 | 29 | |
1,6 | 34,5
|
|
A | B | |
1,8 | 40 | |
2,0 | 46 | |
2,2 | 52 | |
2,4 | 58,5
|
|
A | B | |
2,6 | 65 | |
2,8 | 72 | |
3,0 | 79,5 | |
3,2 | 87
|
Z powyższych rozważań wynika, że wiązania jonowe tworzy się najłatwiej przez połączenie atomów pierwiastków o małej energii jonizacji, wykazujących dużą łatwość oddawania elektronów zewnętrznych, z atomami pierwiastków o wysokim powinowactwie elektronowym.
Wiązanie jonowe między dwoma jonami może być zrealizowane jedynie w fazie gazowej. Ze względu na to, że wiązanie jonowe polega na oddziaływaniu elektrostatycznym o symetrii kulistej, w przypadku zestalenia substancji w zasięg działania sił elektrostatycznych jonu wchodzą otaczające go jony i w wyniku tego powstaje sieć jonowa. W tym przypadku słuszniej jest mówić o więzi jonowej niż o wiązaniu jonowym.
W sieci jonowej istnieje tendencja do jak najściślejszego ułożenia jonów w przestrzeni.
Przy obliczaniu energii sieci krystalicznej przyjmuje się, że poszczególne jony są sztywnymi kulami o określonych promieniach, obdarzonymi ładunkami elektrycznymi.
Uważanie jonów za sztywne kule nie jest zbyt dużym uproszczeniem, a to z tego względu, że przy wzajemnym zbliżaniu dwu jonów wywołanym przyciąganiem, powłoki elektronowe przeciwstawiają się zbytniemu wzajemnemu przenikaniu. Opór ten rośnie gwałtownie w miarę zmniejszania odległości między jonami. Tak więc odstęp między jonami w sieci krystalicznej nie jest sumą promieni sztywnych kuł, ale odległością wynikającą z równowagi między siłami przyciągania a siłami odpychania.
W sieciach jonowych trudno mówić o cząsteczkach chemicznych, gdyż cała sieć jonowa stanowi jakby makrocząsteczkę powiązaną siłami elektrostatycznymi. Prawidłowości w ramach tej sieci zależą od wymiarów geometrycznych i ładunków elektrycznych tworzących ją jonów. Do obliczenia energii sieci krystalicznej konieczna jest znajomość odległości między jonami oraz typ sieci jonowej.
Pierwsze obliczenia tego rodzaju wykonał E. Madelung (rys. 2.15).
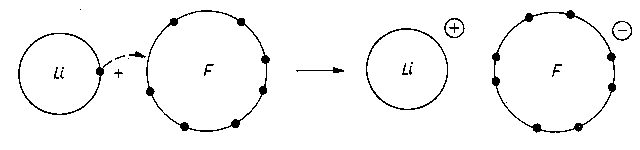 |
Rys. 2.15. Model wiązania jonowego
|
Energia sieci krystalicznej wg wzoru Madelunga
gdzie: e1, e2, - ładunki jonów, r - odległość między jonami, NL - liczba Loschmidta 6,023 • 1023, A - stała Madelunga (sumowanie potencjałów wszystkich jonów sieci).
Energia sieci krystalicznej wg wzoru Borna
gdzie: w1, w2-wartościowość jonów, e - ładunek elektronu, R = ra+rk - odległość między kationem a anionem.
Energia sieci krystalicznej wg wzoru Kapustinskiego
|
U = 256,1 | S n w1 w2
rk + ra | |
U = 287,2 | S n w1 w2
rk + ra | (1- | 0,345
rk + ra | ) |
|
gdzie: S n - liczba jonów w danym typie związku, gdzie: rk + ra - suma promieni jonowych.
2.3.3. Wiązanie koordynacyjne
Wiązanie koordynacyjne jest zwane również wiązaniem semipolarnym, wiązaniem kowalencyjnym lub wiązaniem donorowo-akceptorowym. Jest to specjalny rodzaj wiązania kowalencyjnego, w którym elektrony wiążące nie pochodzą od obydwu łączących się ze sobą atomów, lecz tylko od jednego z nich. Powstaje ono wówczas, gdy jeden atom, zwany donorem ma swobodną parę elektronową, drugi zaś, zwany akceptorem, ma niezapełnione orbity elektronowe i dodatnie powinowactwo do elektronów. Przy tworzeniu wiązania koordynacyjnego atom donorowy oddając swoje elektrony do wytwarzania wiązania uzyskuje dodatni ładunek, natomiast akceptorowy ma nadmiar elektronów w stosunku do ładunku jego jądra i uzyskuje ładunek ujemny. Stąd pochodzi nazwa wiązanie semipolarne, czyli półjonowe.
Jeżeli w wyniku związania wiązaniem semipolarnym powstają jony np. amonowe, to wszystkie cztery wiązania N-H są spolaryzowane w jednakowym stopniu, a ładunek jonu rozmieszcza się na całym kompleksie (rys. 2.16). Na rysunku tym podano przykładowo wykorzystanie wolnej pary elektronowej azotu w amoniaku do tworzenia wiązań semipolarnych z atomami innych pierwiastków.
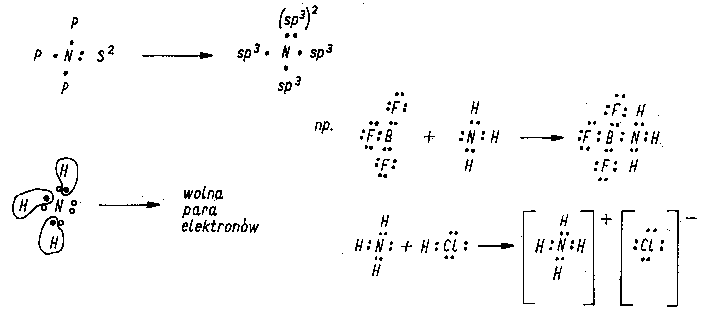 |
Rys. 2.16. Model wiązania semipolarnego
|
Trwałość wiązania semipolarnego zależy między innymi od wartości różnicy poziomów energetycznych niezapełnionej orbity akceptora i wolnej pary elektronowej donora oraz od rodzaju atomów donora i akceptora.
Zaznaczyć należy, że wiązanie semipolarne może występować zarówno pomiędzy atomami w cząsteczce, jak i pomiędzy cząsteczkami. Jest ono podstawą tworzenia różnego rodzaju związków kompleksowych.
2.3.4. Wiązanie wodorowe
Wiązanie wodorowe, zwane również wiązaniem protonowym lub mostkiem wodorowym, jest specyficznym rodzajem wiązania, które może być wiązaniem wewnątrzcząsteczkowym, jak również wiązaniem międzycząsteczkowym. Elementem powodującym wystąpienie tego rodzaju wiązania jest jądro wodoru, czyli proton, który ze względu na swe bardzo małe wymiary (jest mniejszy on od wszystkich atomów i jonów) może przenikać nawet w głąb powłoki elektronowej silnie elektroujemnego atomu, wskutek czego oddziaływanie między nim a elektronami atomu znajdującymi się w zasięgu jego działania jest silne i ma charakter elektrostatyczny. Odkształcenie przez proton powłoki elektronowej atomu połączonego z nim wiązaniem wodorowym nadaje temu wiązaniu charakter kierunkowy, a więc częściowo kowalencyjny. Z tego względu wiązanie wodorowe uważa się za wiązanie typu pośredniego między wiązaniem atomowym i jonowym. Wiązania wodorowe są często spotykane w związkach organicznych i w niektórych związkach nieorganicznych. Odpowiedzialne są one za asocjację wody, alkoholi, kwasów i in. Skłonność pierwiastków elektroujemnych do tworzenia wiązań wodorowych przedstawiono na rys. 2.17.
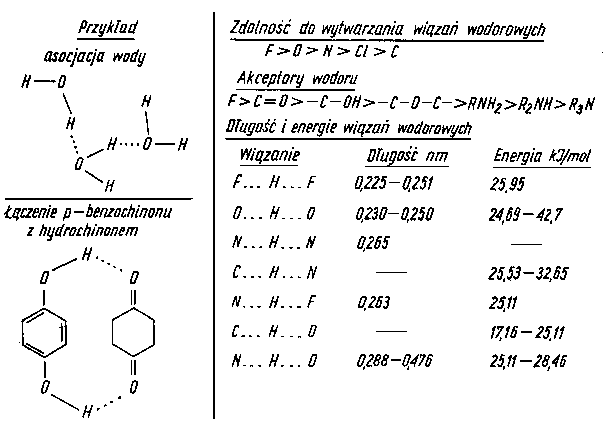 |
Rys. 2.17. Model wiązania wodorowego
|
2.3.5. Wiązanie metaliczne
Wiązanie metaliczne jest charakterystycznym rodzajem wiązania dla metali. Bardziej właściwym terminem na określenie tego rodzaju wiązania byłby termin więź metaliczna, gdyż wiązanie to występuje nie między dwoma lub kilkoma atomami metalu, lecz cały element metalowy można uważać za jedną makrocząsteczkę.
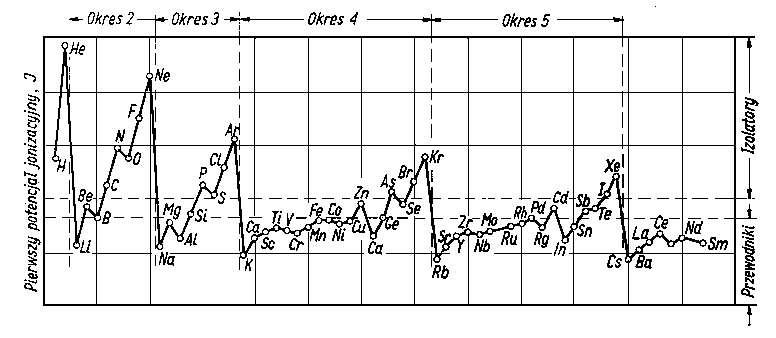 | |
Rys. 2.18. Pierwsze potencjały jonizacyjne pierwiastków w funkcji kolejności pierwiastków w układzie okresowym
|
Do właściwości charakterystycznych metali należą: duża przewodność cieplna i elektryczna. Wiąże się to ściśle z ich budową atomową. Atomy metali mają niewiele elektronów w powłoce zewnętrznej i elektrony te są stosunkowo luźno związane z pozostałą częścią atomu (zrębem atomowym). Luźne związanie elektronów zewnętrznych powoduje, że pierwiastki metaliczne mają małe wartości potencjałów jonizujących. Przejrzyście zależność tę przedstawiono na rys. 2.18.
Własności energetyczne pojedynczego atomu metalu określane są przez własności energetyczne poszczególnych orbitali. Jeżeli metal ze stanu gazowego przechodzi w stan ciekły, a następnie zestala się tworząc siatkę krystaliczną, poszczególne atomy metalu zaczynają podlegać działaniu pól elektrostatycznych zbliżających się do nich innych atomów metalu.
Powoduje to, że elektrony atomów metalu znajdujące się na zewnętrznych powłokach zaczynają stopniowo podlegać działaniu pola elektrostatycznego zbliżających się do nich innych atomów metalu, wskutek czego zostaje osłabione oddziaływanie dodatniego ładunku własnego jądra już i tak osłabionego wskutek ekranowania tego oddziaływania przez otaczające jądro elektronów bliższych powłok, które działają odpychająco na elektrony powłoki zewnętrznej.
W przypadku, gdy oddziaływanie pola elektrostatycznego otaczających atom sąsiednich atomów metalu zrównoważy przyciągające oddziaływanie własnego jądra, elektrony powłoki zewnętrznej przestają być związane z własnym atomem i mogą się swobodnie poruszać pomiędzy innymi atomami (a dokładniej zrębami atomowymi) fazy metalicznej.
Ponieważ w takiej samej sytuacji znajdują się i elektrony wszystkich atomów fazy metalicznej, dlatego też faza metaliczna ,,składa się" z atomów metalu z odszczepionymi elektronami powłoki zewnętrznej, czyli tzw. zrębów atomowych, wokół których poruszają się swobodnie elektrony tworząc gaz elektronowy.
Tak więc fazę metaliczną tworzą zręby atomowe zanurzone w gazie elektronowym. Teoria gazu elektronowego jako części składowej struktury metali została wprowadzona na początku naszego stulecia (1900 r.) przez Drudego bez odpowiedniego uzasadnienia teoretycznego. Chodziło tu przede wszystkim o wyjaśnienie dobrej przewodności elektrycznej i cieplnej metali.
W teorii tej założono, że kryształ metalu składa się z dodatnich jonów metali, których elektrony mogą się swobodnie poruszać pomiędzy jonami, jak gdyby tworzyły rodzaj gazu elektronowego. Spójność kryształu metalu istnieje w wyniku działania sił przyciągania elektrostatycznego pomiędzy dodatnio naładowanymi jonami a ujemnie naładowanym gazem elektronowym. Założono, że elektrony podczas swego ruchu we wnętrzu kryształu podlegają tylko prawom klasycznej mechaniki. Lorentz rozszerzył postulaty wysunięte przez Drudego i zastosował do ruchu elektronów prawa teorii kinetycznej gazów. Zmodyfikowana teoria elektronów swobodnych znana jest pod nazwą teorii Drudego-Lorentza.
Należy zaznaczyć, że w teorii tej pominięto wzajemne odpychane pomiędzy ujemnie naładowanymi elektronami a polem potencjału wytwarzanym przez dodatnie jony zostało uznane za zupełnie jednorodne. Według niej elektrony poruszają się w krysztale bez jakichkolwiek zmian energii, mimo zderzeń z jonami, a prędkości ich w stałej temperaturze są zgodne z prawami rozkładu Maxwella - Boltzmanna.
Teoria Drudego-Lorentza pozwoliła na wyjaśnienie niektórych własności metali, niemniej jednak zasadniczym jej niepowodzeniem były rozbieżności między mierzonymi a przewidywanymi wg tej teorii wartościami ciepła właściwego metali.
Rozwój mechaniki kwantowej pozwolił przystosować teorię Drudego-Lorentza do teorii budowy metali. Koncepcja gazu elektronowego pozostała, ale zastosowano do niej prawa mechaniki kwantowej i statystykę kwantową Fermiego-Diraca. W wyniku tego znacznie zmodyfikowano poprzednią teorię. W statystyce kwantowej Fermiego-Diraca został uwzględniony fakt, że elektrony są obdarzone spinem i że dla każdego stanu energetycznego atomu mogą istnieć tylko dwa elektrony o antyrównoległych spinach.
Ponadto przyjęto założenie, że potencjał pola elektrycznego, w którym porusza się elektron nie jest stały (jak to przyjmowano w teorii Drudego-Lorentza), lecz zmienia się w przestrzeni fazy metalicznej okresowo zgodnie z rozmieszczeniem jonów (zrębów atomowych) w sieci kryształu metalu. Jednowymiarowy model metalu oparty na takim założeniu przedstawiono na rys. 2.19.
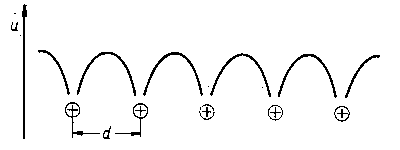 |
Rys. 2.19. Jednowymiarowy model metalu z rozkładem potencjału: u - energia potencjalna elektronu, d-odległość międzywęzłowa
|
Elektron poruszający się w pobliżu zrębu atomowego ma mniejszą średnią energię potencjalną, gdyż dłużej przebywa on w pobliżu jądra, natomiast jego średnia energia kinetyczna jest większa, ponieważ przestrzeń, w której się on porusza jest bardziej ograniczona niż w przypadkach elektronu poruszającego się dalej od jądra (zrębu atomowego).
Elektrony poruszające się swobodnie w fazie metalicznej nie mogą jej opuścić, gdyż są powstrzymywane przez barierę potencjału pola elektrostatycznego wytwarzanego przez dodatnio naładowane zręby atomów metalu. Dla pokonania tej bariery potencjału elektrony musiałyby otrzymać dodatkową energię zwaną energią wyjścia elektronu.
Z powyższych przyczyn w rozważaniach teoretycznych przyjmuje się często, że elektron w fazie metalicznej porusza się jakby w zamkniętym pudle ograniczonym barierą potencjału.
W uproszczonych rozważaniach przyjmuje się jednowymiarowe pudło potencjału, a w rozważaniach bardziej złożonych pudło trójwymiarowe, a więc przestrzenne. Nie należy jednak zapominać o tym, że w mechanice kwantowej elektron uważa się za falę elektronową o określonej długości
gdzie: h - stała Plancka, m - masa elektronu, v - prędkość elektronu, p - pęd elektronu.
Zamiast fali można wprowadzić pojęcie liczby falowej k (równej liczbie długości fali zawartej w pełnym okresie), mającej charakter wektora
|
k = |
2p
l |
k = |
2 p
h |
mv | (2.4) |
Jak widać ze wzoru liczbie falowej k odpowiada impuls elektronu.
Energia kinetyczna E swobodnego elektronu wynosi
|
E = |
1
2 |
m v2 = |
1
2 |
m |
( |
h k
2 p m |
)2 |
= |
h2 k2
8 p2m
| (2.5) |
Zależność między energią kinetyczną a liczbą falową przedstawia parabola.
Przy założeniu jednowymiarowego pudła potencjału, jako jednowymiarowego modelu metalu, zmieszczą się w nim ze względu na warunki graniczne (odbicie fal elektronowych od ścian pudła) tylko wszystkie fale stojące o długości związanej prostą zależnością z długością pudła L, a mianowicie
|
l = |
2 L
n |
= |
2 p
k |
; |
k = n |
2 p
2 L
| (2.6)
|
gdzie: n - są liczbami całkowitymi odpowiadającymi liczbom kwantowym.
Po wprowadzeniu obliczonej wartości k do wzoru na energię kinetyczną otrzymuje się wyrażenie
|
E = |
h ² n ²
8 p ² m |
= |
h ² k ²
8 m L²
| (2.7)
|
Ten sam wynik można by uzyskać z równania Schrödingera dla jednej zmiennej
|
¶2 y
¶x2 | + |
8 p2 m
h2 | E y = 0
| (2.8)
|
Zależność E od k komplikuje się wskutek istnienia okresowego pola potencjału wytwarzanego przez dodatnio naładowane zręby atomowe.
Ten wpływ można utożsamiać z odbiciem fal elektronowych od określonych płaszczyzn sieciowych, gdyż jak już wspomniano pole potencjału w sieci krystalicznej układa się tak, jak rozmieszczenie zrębów atomowych w węzłach sieci przestrzennej. Odbicie to podlega prawu Bragga
Wprowadzając liczby falowe zmiany pędu elektronowego wywołane odbiciem fali otrzymujemy
gdzie: d - odległość między płaszczyznami sieciowymi, q - kąt Bragga.
|
Takie nieciągłości występują więc przy
k1 = |
p
d1 sinq |
, k2 = |
p
d2 sinq
|
Na skutek tego w przebiegu funkcji E = f(k) istnieją przerwy, to znaczy, że przy niektórych wartościach E liczba falowa k przyjmuje wartości urojone. Istnieją więc obok obszarów dozwolonych obszary zakazane dla impulsów elektronów. W ich pobliżu krzywa odbiega od kształtu parabolicznego (rys. 2.20).
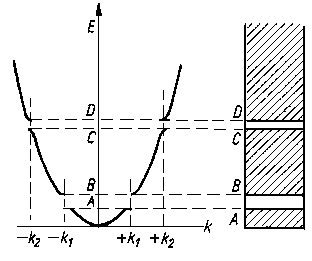 |
Rys. 2.20. Zależność energii kinetycznej od liczby falowej
|
Przechodząc od jednowymiarowego modelu metalu do modelu trójwymiarowego, w którym rozprzestrzenia się fala elektronowa, otrzyma się również nieciągłości energetyczne zależne od typu sieci. Granice tych nieciągłości dla trójwymiarowej sieci utworzą trójwymiarową bryłę geometryczną o określonej symetrii. Jest to tzw. pierwsza strefa Brillouina, po której następują dalsze strefy z nią współśrodkowe. Między strukturą sieci metali a kształtem stref Brillouina zachodzi ścisła zależność, przez co zostaje ustalona również zależność między strukturą elektronową a strukturą sieci krystalicznej. Kształty pierwszej i drugiej strefy Brillouina dla kilku struktur przedstawiono na rys. 2.21 (12).
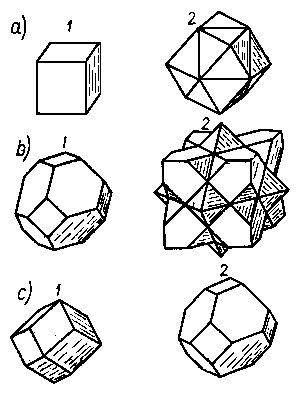 |
Rys. 2.21. Pierwsza i druga strefa Brillouina:
a) sieci regularnej,
b) sieci A1,
c) sieci A2;
pierwsza strefa jest zawarta w obrębie poliedru 1,
druga - między poliedrem 2 a 1
|
Przy rozpatrywaniu budowy metali oprócz przedstawionych powyżej zagadnień wpływu okresowego pola potencjału sieci na charakter ruchu swobodnych elektronów ważny jest również stan energetyczny elektronów w przypadku, gdy swobodne atomy metalu zbliżające na coraz to mniejszą odległość i zaczyna się wzajemne oddziaływanie powłok elektronowych zbliżających się do siebie atomów.
W pojedynczym atomie elektrony mogą zajmować tylko określone poziomy energetyczne, przy czym liczba elektronów na danym poziomie energetycznym jest ograniczona zasadą Pauliego.
W przypadku, gdy do pojedynczego atomu zaczynają się zbliżać inne atomy (co występuje przy krzepnięciu metalu), to wskutek wzajemnego oddziaływania powłok elektronowych pojedyncze poziomy energetyczne zaczynają się rozszczepiać (rozmywać) tak, że zachodzą wzajemnie na siebie, tworząc w rezultacie ciągłe pasmo energetyczne. Pasma energetyczne mogą nakładać się na siebie, np. pasmo s i p powłoki L. Wówczas elektrony tej powłoki mają do pewnego stopnia mieszany charakter elektronów s, p (elektrony zhybrydyzowane), a w przypadku nałożenia się pasma d (w metalach przejściowych) mają charakter elektronów s, p, d. Szerokość pasma energetycznego jest tym większa im większa liczba atomów oddziałuje na siebie wzajemnie z małych odległości, współmiernych z promieniem atomu, a więc takich jakie występują w sieci krystalicznej. Jeżeli liczba oddziałujących na siebie atomów wynosi N, to elektrony w obrębie dopuszczalnych energetycznie pasm mają do dyspozycji N poziomów energetycznych położonych tak blisko siebie, że praktycznie tworzą one ciągłe pasmo energetyczne. Rozszczepianie poziomów energetycznych dla atomu sodu w pasma energetyczne przedstawiono schematycznie na rys. 2.22.
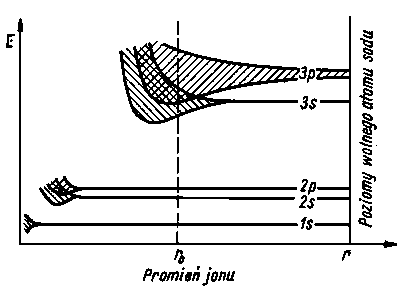 |
Rys. 2.22. Rozszczepienie poziomów energetycznych wg Joffego
|
Na osi rzędnych jest zaznaczona energia, a na osi odciętych - odległość r pomiędzy atomami (ro - oznacza odległość atomów w metalicznym sodzie). Jak widać z rysunku rozszczepieniu najłatwiej ulegają poziomy energetyczne 3s i 3p odpowiadające elektronom położonym najdalej jądra. Najsłabiej natomiast rozszczepiają się poziomy odpowiadające elektronom położonym najbliżej jądra atomowego. Przedstawione na rys. 2.22 poziomy 3s i 3p uległy tak silnemu rozszczepieniu, że powstałe z nich pasma zachodzą na siebie tworząc w istocie jedno wspólne pasmo. Ze względu na to, że na poziomie 3s występował w niewzbudzonych atomach sodu tylko jeden elektron, a na poziomie 3p nie ma elektronów, powstałe przez rozszczepienie wspólne pasmo energetyczne jest tylko częściowo wypełnione elektronami. W takich warunkach jest możliwe przemieszczanie elektronów po obdarzeniu ich dodatkową energią kinetyczną. Sprowadza się ono do przesunięcia elektronu z danego poziomu energetycznego na położony w pobliżu nie zajęty poziom wyższy. Tak np. już po przyłożeniu do metalu małego napięcia elektrycznego zaczyna przez metal płynąć prąd elektryczny. Najłatwiej jest przesunąć elektrony leżące w pobliżu tzw. poziomu Fermiego, tj. poziomu, do którego pasma energetyczne są wypełnione elektronami w temperaturze zera absolutnego.
W przypadku gdy pasma energetyczne nie zachodzą na siebie, a zwłaszcza gdy są oddzielone od siebie szerokimi pasami wzbronionymi, przesunięcie elektronu do pasma energetycznego, w którym mógłby się on poruszać (pasma przewodnictwa), wymaga obdarzenia go bardzo dużą energią. Jakiekolwiek pośrednie wartości energii są niedopuszczalne.
Jeżeli odstęp między pasmem podstawowym a pasmem przewodności jest duży, to dla nadania elektronowi dostatecznie dużej energii wystarczającej do jego poruszania się wewnątrz sieci krystalicznej (aby kryształ mógł przewodzić prąd elektryczny), konieczne jest albo przyłożenie bardzo znacznego napięcia albo też ogrzanie kryształu do wysokiej temperatury. W przeciwnym przypadku kryształ będzie doskonałym izolatorem (rys. 2.23).
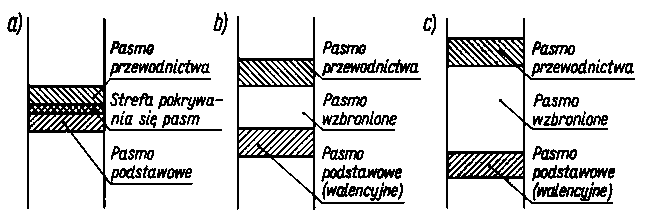 |
Rys. 2.23. Schemat poziomów energetycznych w:
a) metalu,
b) półprzewodniku,
c) izolatorze
|
Ciała stałe, w których poszczególne atomy są powiązane ze sobą wiązaniami homeopolarnymi zużywają w tym celu swoje elektrony walencyjne. Elektrony wiążące ze sobą sąsiednie atomy są zlokalizowane i nie mogą się poruszać swobodnie wewnątrz ciała stałego. Pozostają one w swych wiązaniach nawet wtedy, gdy z zewnątrz przykłada się znaczne napięcie elektryczne (nie przekraczające jednak pewnej granicznej wartości). W tych warunkach prąd elektryczny nie popłynie przez kryształ. Pojawić się on może dopiero wtedy, gdy wskutek termicznych drgań atomów lub przyłożenia bardzo wysokiej różnicy potencjałów nastąpi wyrwanie elektronu z wiązania. Tak więc w ciele stałym, w którym wszystkie wiązania pozostają w stanie nienaruszonym, pasmo podstawowe jest całkowicie wypełnione, a pasmo przewodnictwa puste.
Wyrwanie elektronu z wiązania odpowiada przeniesieniu go z pasma podstawowego do pasma przewodnictwa z równoczesnym pozostawieniem jednego nie obsadzonego atomu kwantowego w paśmie podstawowym.
Pomiędzy tymi dwoma rodzajami ciał stałych - przewodnikami i izolatorami istnieje jeszcze rodzaj ciał o charakterze pośrednim zwanych półprzewodnikami. Jakościowo półprzewodniki nie różnią się od izolatorów. Różnica ilościowa polega na tym, że odległość pasma podstawowego od pasma przewodnictwa w tym przypadku nie jest duża, zazwyczaj rzędu 1,6 • 10 -19 J (l eV). Przekroczenie tej odległości jest łatwiejsze niż przekroczenie pasma zakazanego w przypadku izolatora.
Wskutek drgań cieplnych sieci przestrzennej i zderzeń występujących w niej atomów, niektóre elektrony nawet w temperaturze pokojowej uzyskują dostatecznie dużą energię, aby przejść do pasma przewodnictwa. Poruszanie się w ciele stałym elektronów, które znalazły się w paśmie przewodnictwa elektronów wolnych jest łatwe. Do tego celu wystarcza przyłożenie małego napięcia. Z chwilą pojawienia się elektronów w paśmie przewodnictwa ciało przestaje być izolatorem i zaczyna przewodzić prąd. Elektron opuszczając pasmo podstawowe pozostawia w nim jeden nie obsadzony poziom energetyczny, tzw. dziurę. Poziom ten może być zajęty przez którykolwiek z pozostałych elektronów pasma podstawowego. Do tego celu na ogół wystarcza już tylko mała energia aktywacji. Elektron zajmujący dziurę pozostawia znów po sobie nie zajęty poziom energetyczny, czyli nową dziurę itd. Pojawienie się dziury w siatce krystalicznej umożliwia przenoszenie elektronów. Przesuwanie się dziury, polegające na przeskokach elektronów, formalnie może być rozpatrywane jako przesuwanie się elementarnego ładunku dodatniego. W ciele nie zawierającym ani żadnych defektów sieciowych, ani żadnych domieszek, nawet w podwyższonej temperaturze, liczba wolnych elektronów w paśmie przewodnictwa i liczba dziur w paśmie podstawowym jest mała, a więc małe jest przewodnictwo elektryczne, które jest proporcjonalne do nośników prądu.
Należy tu zaznaczyć, że na przewodnictwo ma wpływ nie tylko temperatura i odstęp pasma podstawowego od pasma przewodnictwa, lecz również w bardzo znacznym stopniu nawet małe ilości różnego rodzaju zanieczyszczeń i zaburzeń sieci przestrzennej, które stają się źródłem dodatkowych nośników prądu: wolnych elektronów lub dziur.
Rolę takich zanieczyszczeń mogą spełniać np. obce atomy lub też atomy wchodzące w skład danej substancji, lecz występujące w nadmiarze w stosunku do idealnego składu stechiometrycznego. Pojawienie się tych zaburzeń prowadzi do powstania nowych dozwolonych poziomów w widmie energetycznym ciała stałego w paśmie wzbronionym (rys. 2.24).
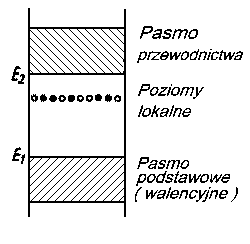 |
Rys. 2.24. Poziomy lokalne w widmie energetycznym ciała stałego;
- poziomy zajęte przez elektrony,
- poziomy nie zajęte przez elektrony
|
Poziomy te zwane poziomami lokalnymi mogą być całkowicie lub częściowo zapełnione i mogą dostarczać elektronów (poziomy donorowo) lub pobierać elektrony (poziomy akceptorowe).
Oprócz poziomów lokalnych spowodowanych obecnością domieszek, mogą się pojawiać w paśmie wzbronionym (jak to wykazał w swoich obliczeniach I. E. Tamm) również tzw. poziomy powierzchniowe, zwane najczęściej poziomami Tamma. Poziomy takie powstają na powierzchni kryształu, gdzie okresowo potencjał sieci przestrzennej przechodzi w stały potencjał ośrodka otaczającego ciało stałe. Każdemu atomowi znajdującemu się na powierzchni, oprócz jego normalnego poziomu, odpowiada jeden poziom powierzchniowy. Na poziomy te przechodzą elektrony z pasma podstawowego, pozostawiając w nim wolne dziury.
Przedstawione powyżej w najogólniejszym jakościowym zarysie podstawowe pojęcie teorii pudła potencjału oraz teorii pasmowej ciała stałego, a zwłaszcza ciała metalicznego prowadzą do podobnych wniosków. Wynika z nich, że w metalu elektrony mają dużą swobodę poruszania się, ale są dostępne dla nich tylko określone stany energetyczne charakteryzujące własności fizyczne metali (np. przewodność elektryczna, cieplna itd.).
Przedstawione teorie stanu metalicznego mają charakter fizyczny. Brak jest dotąd właściwej teorii więzi metalicznej w sensie chemicznym. Teoria taka powinna wyjaśnić zmiany właściwości pierwiastków metalicznych w grupach i okresach, następnie powinna odzwierciedlać zachowanie się pierwiastków w stopach metalicznych oraz uzasadnić istnienie faz i związków międzymetalicznych. Próby ustalania takiej teorii (Pauling) zawiodły, gdyż doprowadziły do wniosków sprzecznych z ogólnie przyjętymi pojęciami chemicznymi i sprzecznych z wynikami badań fizycznych. Z tego względu w obecnym stanie rozwoju nauki można mówić tylko o fizycznych teoriach stanu metalicznego.
2.4. Siły międzycząsteczkowe
W życiu codziennym mamy do czynienia nie z atomami lub cząsteczkami, lecz z ciałami złożonymi z ogromnej liczby atomów lub cząsteczek. Wiele typów wiązań, za pomocą których atomy wiążą się w cząsteczki, może również posłużyć do wiązania cząsteczek w jedną wielką makrocząsteczkę.
Oprócz już omówionych rodzajów wiązań należy zaznaczyć, że między cząsteczkami występują również specyficznego rodzaju oddziaływania zwane siłami międzycząsteczkowymi lub siłami Van der Waalsa. Siły te działają między cząsteczkami substancji gazowych i ciekłych, jak również między cząsteczkami w sieciach kryształów cząsteczkowych. Siły Van der Waalsa najmocniej działają w kryształach i cieczach, a najsłabiej w gazach, gdyż są tym większe, im bliżej siebie znajdują się cząsteczki.
W cieczach wskutek silnego przyciągania cząsteczek często występuje asocjacja, przez co zacierają się granice poszczególnych cząsteczek. Wiązania międzycząsteczkowe polegają na wzajemnym oddziaływaniu pola elektrycznego sąsiadujących ze sobą cząsteczek, przy czym nie ma przesunięć elektronów między cząsteczkami, lecz tylko wewnątrz cząsteczek oddziaływujących pomiędzy sobą.
Siły międzycząsteczkowe można podzielić na cztery zasadnicze grupy: siły dyspersyjne (siły Londona), siły konformacyjne, siły orientacyjne (siły Keesoma) oraz siły indukcyjne (siły Debye'a) (tabl. 2.6).
Piątym rodzajem sił międzycząsteczkowych jest wiązanie wodorowe, jeżeli występuje między cząsteczkami, a nie w obrębie jednej cząsteczki.
Tablica 2.6. Rodzaje sil międzycząsteczkowych
 |
2.4.1. Siły dyspersyjne
Siły dyspersyjne (siły Londona) nazwę swoją zawdzięczają powiązaniu ze zjawiskiem dyspersji optycznej i dlatego London nazwał je siłami dyspersyjnymi. Są one wynikiem tworzenia dipoli elementarnych wskutek ruchu elektronów wokół jądra. Atom jest obojętny elektrycznie wtedy, gdy ma zrównoważone wzajemnie ładunki dodatnie i ujemne oraz gdy ładunki te są względem siebie przestrzennie symetrycznie rozłożone. Jeżeli wyobrazimy sobie dwa najprostsze atomy zbliżone do siebie, składające się z jądra i tylko jednego elektronu, to innego rodzaju oddziaływanie wystąpi między tymi atomami, gdy elektrony tych dwóch atomów znajdą się na orbitach na przeciw siebie, a inne gdy znajdą się po przeciwnych stronach orbit. Te różnice w rozkładzie ładunków elektrycznych, wynikające z faz poruszania elektronów wokół jądra, powodują powstawanie dipoli chwilowych (fluktuujących). Takich elementarnych chwilowych dipoli w atomie jest tyle, ile elektronów ma atom. Wypadkowe działanie na zewnątrz wszystkich szybkozmiennych dipoli elementarnych wywołuje powstawanie pola elektrycznego działającego na sąsiednie cząsteczki. Działanie szybkozmiennych dipoli wywołuje powstawanie szybkozmiennych momentów dipolowych w sąsiadujących cząsteczkach, przez co przyciągają się one wzajemnie. Tak więc na skutek stałego ruchu elektronów w atomach, elektrony te są w każdej chwili elektrycznie niesymetryczne i mają momenty dipolowe, które średnio w czasie kompensują się do zera. Siły dyspersyjne mają ograniczoną strefę działania, gdyż występują tylko przy dostatecznie dużym zbliżeniu cząstek. Każda cząsteczka może jednocześnie oddziaływać na wiele innych cząsteczek znajdujących się w dostatecznie małej odległości. Przyciąganie siłami dyspersyjnymi jest odwrotnie proporcjonalne do r6 (gdzie r-odległość między środkami mas jąder atomów cząsteczek sąsiadujących). Maleje ona bardzo szybko, gdy cząsteczki oddalają się od siebie.
Oddziaływanie dyspersyjne zwane jest również oddziaływaniem elektrokinetycznym.
2.4.2. Siły konformacyjne
Chwilowy moment dipolowy i związane z nim oddziaływanie elektrostatyczne może być wynikiem nie tylko chwilowych zmian we wzajemnym położeniu elektronów (siły dyspersyjne), ale również zmian w położeniu atomów lub też całych ich grup stanowiących poszczególne człony cząsteczki. Ich rotacja wokół wiązania oraz zmiana usytuowania przestrzennego nazywa się konformacją (rys. 2.25).
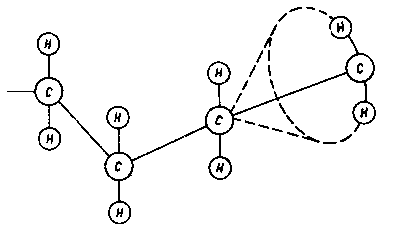 |
Rys. 2.25. Model rotacji członu łańcucha węglowodorowego
|
Konformacja wywołuje zmiany w polu elektrostatycznym poszczególnych członów cząsteczki; oddziaływanie międzycząsteczkowe, jakie przy tym powstaje, ma nazwę sił konformacyjnych. Konformacja może występować nie tylko w przypadku cząsteczek łańcuchowych (rys. 2.25), lecz również i w przypadku związków pierścieniowych o wiązaniach p. Na rys. 2.26 i 2.27 przedstawiono konformacje pierścienia cykloheksanu. Obecność wiązań typu p blokuje możliwość rotacji (patrz rys. 2.11).
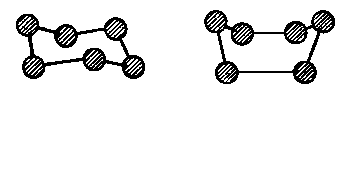 |
Rys. 2.26. Dwie konformacje pierścienia cykloheksanu o kątach 109,5° pomiędzy wiązaniami węglowodorowego
|
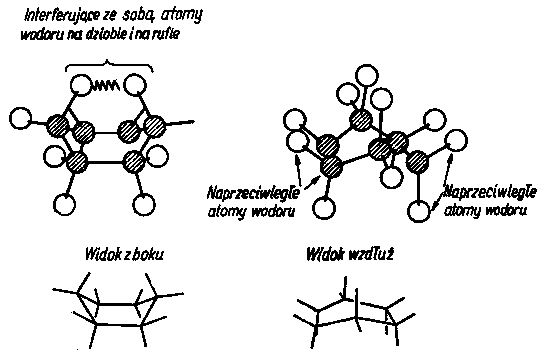 |
Rys. 2.27. Konformacja łódkowa cykloheksanu;
- - atomy H,
- - atomy C
|
Z konformacją wiążą się różnice w stanie energetycznym cząsteczki (rys. 2.28).
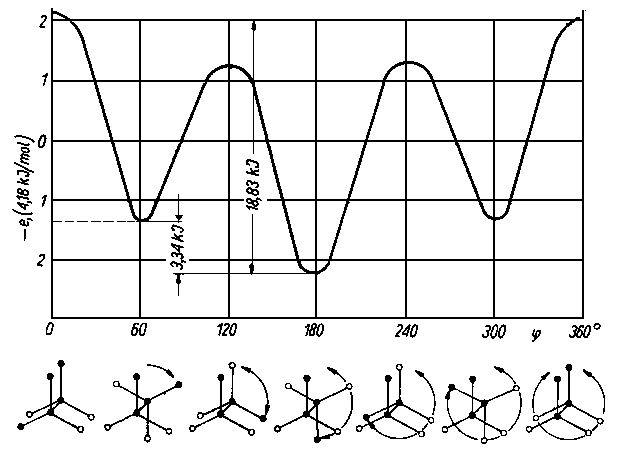 |
Rys. 2.28. Zmiana energii e cząsteczki n-butanu w zależności od kąta obrotu j
|
Siły Londona i siły konformacyjne są wielkościami addytywnymi, tak że mimo małych wartości tych sił ich suma w przypadku dużych cząsteczek powoduje silne oddziaływanie między cząsteczkami (np. dla polimerów).
2.4.3. Siły orientacyjne
Siły orientacyjne (siły Keesoma) są to siły typu elektrostatycznego występujące między cząsteczkami, które są trwałymi dipolami. Trwałym dipolem nazywamy taką cząsteczkę, w której ładunki elektryczne dodatnie i ujemne są rozmieszczone niesymetrycznie. Punkt, w którym jest skupiony ładunek dodatni dipola nazywa się jego biegunem dodatnim, a punkt, w którym jest skupiony jego ładunek ujemny - biegunem ujemnym. Prostą łączącą oba bieguny nazywa się osią dipola. Iloczyn bezwzględnej wartości e ładunku jednego z biegunów dipola i odległości / między biegunami nazywa się momentem dipolowym
Jednostką momentu dipolowego jest kulombometr (C • m).
Moment dipolowy interpretuje się wektorem, przypisując mu kierunek wzdłuż osi dipola i zwrot od bieguna ujemnego do dodatniego.
Moment dipolowy cząsteczki jest sumą wektorową momentów dipolowych jej elementów składowych. Na wypadkowy moment dipolowy składają się atomowe momenty dipolowe, momenty dipolowe wiązań i momenty dipolowe grup atomów, zależne od ich wzajemnego usytuowania w przestrzeni.
Moment dipolowy atomowy wynika z niesymetryczności rozkładu elektronów (a więc ładunków) wewnątrz atomu wskutek hybrydyzacji elektronów, występowania elektronów w postaci uwspólnionej z innymi atomami (wiązania) lub też w postaci wolnej.
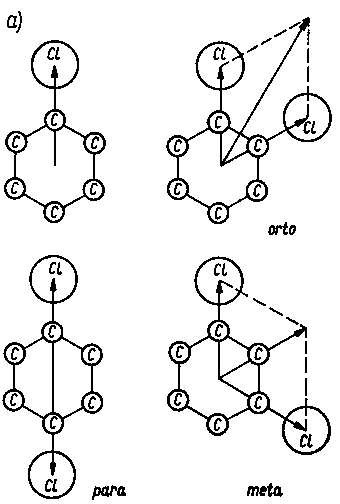 | 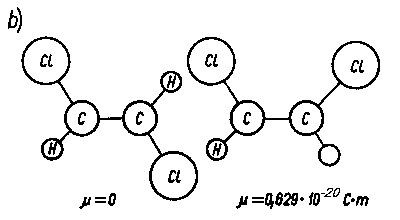
Rys. 2.29 Momenty dipolowe cząsteczek µ:
- dodawanie wektorowe momentów dipolowych µ wiązań w dwuchlorobenzenie,
- wpływ położenia podstawnika chlorowego w dwuchloroetylenie na wartość momentu dipolowego
|
Moment dipolowy wiązania powstaje wówczas, gdy dwa wiążące się ze sobą atomy mają różną elektroujemność. Przez elektroujemność pierwiastka rozumie się tendencje atomów tego pierwiastka do pobierania elektronów. Względna elektroujemność pierwiastka została określona przez Paulinga (patrz str. 37).
Przy wiązaniu kowalencyjnym utworzonym z równomiernie uwspólnionych elektronów nie występuje żaden moment dipolowy, natomiast przy wiązaniu jonowym, połączonym z całkowitym przeniesieniem elektronu z jednego atomu na drugi, występuje jednostkowy moment dipolowy.
Zazwyczaj para elektronów wiązania utworzonego pomiędzy różnymi atomami nie jest uwspólniona równomiernie. Atom o większej elektroujemności w większym stopniu sprzęga ze sobą wiążącą parę elektronową ze względu na silniejsze przyciąganie przez niego elektronów.
Im większa jest różnica w elektroujemności atomów wiążących się wzajemnie, tym większa jest nierównomierność uwspólniania pary elektronowej. Powstaje w ten sposób cząstkowy ładunek, który oznacza się znakami d+ i d- umieszczonymi nad symbolami atomów, np.
Wartość tego cząstkowego ładunku określa się zazwyczaj procentowo, przyjmując dla całkowicie jonowego wiązania 100%, a dla całkowicie kowalencyjnego 0%. Powiązanie między wartościami względnej elektroujemności pierwiastków a charakterem jonowym wiązań pojedynczych, wyrażonym w procentach, przedstawiono w tabl. 2.4.
Należy zaznaczyć, że nawet w przypadku, gdy obydwa atomy tworzące wiązania mają jednakową elektroujemność, może wystąpić tzw. kowalencyjny moment dipolowy, jeżeli atomy te są różnej wielkości. Ponieważ wiązanie powstaje na „peryferii" atomu, dlatego też wiążąca para elektronowa znajduje się bliżej jądra atomu mniejszego, a więc dodatni ładunek jąder nie zostaje wskutek tego w pełni wyrównany, natomiast elektrony wiążące spowodują „nadkompensację" ładunku dodatniego jądra atomu mniejszego. W wyniku tego atom mniejszy zyskuje ładunek ujemny, a większy dodatni.
Oprócz momentów dipolowych atomowych oraz wiązaniowych na wypadkowy moment dipolowy cząsteczki zasadniczy wpływ ma przestrzenne rozmieszczenie atomów lub grup atomów w cząsteczce. Cząsteczki o budowie symetrycznej nie mają momentu dipolowego, natomiast cząsteczki zbudowane niesymetrycznie mają zawsze moment dipolowy.
Grupy cząsteczek niepolarnych w pewnych warunkach mogą wykazywać własności polarne. Tak np. pochodne węglowodorów o dużej liczbie atomów chloru, mające budowę symetryczną, nie są zupełnie niepolarne, lecz tworzą tzw. multipole (kwadrupole, oktupole), w których siły działające na poszczególne bieguny w jednorodnym polu elektrycznym wzajemnie się znoszą, natomiast w niejednorodnym polu (pochodzącym np. od dipola cząsteczkowego) pojawiają się cechy polarne.
W przeciwieństwie do omówionych uprzednio sił dyspersyjnych (sił Londona), które są niezależne od temperatury, siły orientacyjne (siły Keesoma) maleją bardzo szybko wraz ze wzrostem temperatury, gdyż orientacja dipoli zostaje silnie zaburzona na skutek zwiększania się ruchliwości cząsteczek przy ogrzaniu.
W działaniu sił Keesoma, a więc oddziaływaniu dipol-dipol, może przeszkadzać budowa cząsteczek polarnych. W niektórych przypadkach cząsteczka polarna ma takie rozmiary, że jej część niebiegunowa przeszkadza w zbliżeniu jakiegokolwiek innego dipolu na odległość skutecznego oddziaływania. Mówi się wówczas o zawadach przestrzennych w oddziaływaniu dipolowym. W polu elektrycznym dipole trwałe ulegają orientacji wzdłuż linii pola sił (rys. 2.30).
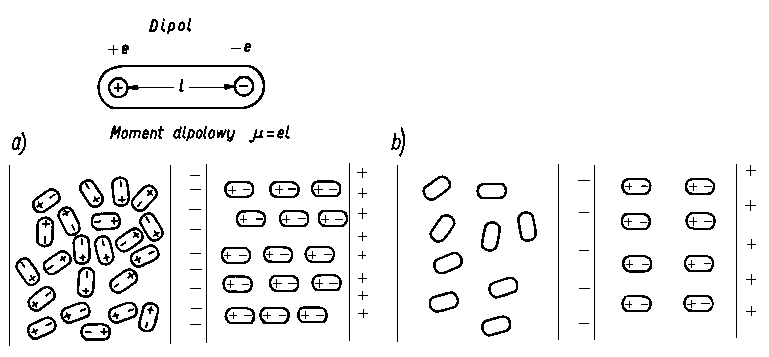
Rys. 2.30. Wpływ pola elektrycznego na dipole trwałe i cząsteczki niepolarne:
- orientacja dipoli trwałych pod wpływem pola elektrycznego,
- polaryzacja indukowana cząsteczek niepolarnychpod wpływem pola elektrycznego; µ = e l - moment dipolowy
|
2.4.4. Siły indukcyjne
Cząsteczki niepolarne, a więc nie mające trwałego momentu dipolowego, gdy znajdują się w zasięgu działania pola elektrycznego stają się dipolami wskutek przesunięcia ładunków elektrycznych wewnątrz cząsteczki. Powstałe w ten sposób dipole są nazywane dipolami indukowanymi. Rozsuwanie ładunków elektrycznych cząsteczki może następować albo w wyniku przyłożonego zewnętrznego pola elektrycznego, albo też w wyniku działania pola elektrycznego dipola trwałego.
Siły występujące przy oddziaływaniu dipol trwały (stały) - dipol indukowany są nazywane siłami indukcyjnymi lub siłami Debye'a.
Rozsuwanie ładunków w cząsteczce niepolarne] i powstawanie dipola indukowanego nazywa się polaryzacją. Rozróżnia się trzy rodzaje polaryzacji: polaryzację elektronową, polaryzację atomową i polaryzację orientacyjną.
Polaryzacja elektronowa polega na przesunięciu orbit elektronowych względem jądra, przy czym wzrasta ona wraz ze wzrostem rozmiarów orbity elektronowej. Im dalej od jądra znajduje się elektron, tym większa jest jego ruchliwość i tym łatwiej poddaje się on działaniu pola elektrycznego. Największą wartością polaryzacji odznaczają się elektrony walencyjne, które są najsłabiej związane z jądrem.
Polaryzacja atomowa polega na przesunięciu względem siebie atomów tworzących cząsteczkę. Polaryzacja elektronowa molowa Pe i polaryzacja atomowa molowa Pa stanowią razem polaryzację deformacyjną molową Pd (zwaną również polaryzacją indukowaną lub polaryzacją przesunięcia
|
Pd = Pe + Pa |
= |
es - 1
es + 2 |
• |
Mc
d |
= |
4
3 |
p N ae |
+ |
4
3 |
p N aa
| (2.11) |
przy czym
|
Pe = |
4
3 |
p N ae; |
Pa = |
4
3 |
p N aa
|
gdzie: es - przenikalność dielektryczna statyczna, Mc - masa cząsteczkowa, d - gęstość substancji, N - liczba Avogadro, ae, aa — współczynniki polaryzacji elektronowej i atomowej.
W polaryzacji deformacyjnej udział polaryzacji atomowej jest stosunkowo niewielki w porównaniu z udziałem polaryzacji elektronowej i wynosi zwykle nie więcej niż 10% polaryzacji elektronowej. Polaryzacja elektronowa i atomowa zanikają wtedy, gdy ustaje działanie pola elektrycznego na niepolarną cząsteczkę.
Polaryzacja orientacyjna polega na orientowaniu trwałych dipoli cząsteczkowych w polu elektrycznym. Cząsteczki substancji mającej trwały moment dipolowy dążą do takiego ustawienia w polu elektrycznym, aby kierunki ich momentów dipolowych były równoległe do kierunku linii pola elektrycznego E, gdyż odpowiada to minimum energii potencjalnej.
Cząsteczki polarne tym trudniej orientują się w polu elektrycznym, im większe mają rozmiary i im większą lepkość ma ośrodek, w którym one występują. Orientacji przeszkadzają również ruchy cieplne cząsteczek, wprowadzające zaburzenia w uporządkowanym ułożeniu cząsteczek wzdłuż linii pola elektrycznego.
Na całkowitą polaryzację molową składa się polaryzacja elektronowa, atomowa i orientacyjna. Wszystkie te trzy składowe są ściśle zależne od częstotliwości przyłożonego pola (rys. 2.31).
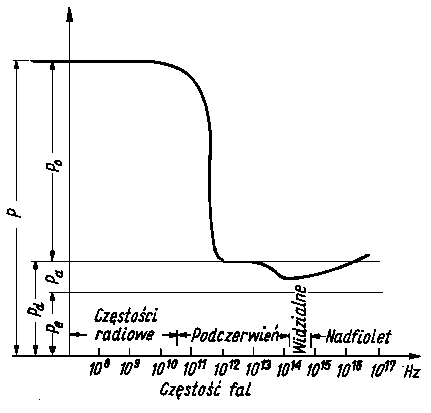 |
Rys. 2.31. Zależność polaryzacji cząsteczki od częstości przesyłanego pola elektromagnetycznego;
- P - polaryzacja,
- Po - polaryzacja orientacyjna,
- Pa - polaryzacja atomowa,
- Pe - polaryzacja elektronowa,
- Pd - polaryzacja deformacyjna
|
Polaryzacja elektronowa zachodzi niezwykle szybko i nadąża za częstotliwością zmian pola nawet wtedy, gdy częstotliwość ta jest wysoka (obszar nadfioletu). Można ją więc uważać za proces pozbawiony bezwładności. Znacznie wolniejszym procesem ze względu na dużą masę jąder atomowych jest polaryzacja atomowa odpowiadająca częstościom drgań z zakresu podczerwieni. Jeszcze wolniejszym procesem jest polaryzacja orientacyjna odpowiadająca częstościom fal radiowych, a więc można ją zaliczyć do powolnych procesów relaksacyjnych.
Do wyznaczenia polaryzacji deformacyjnej (indukowanej) może posłużyć równanie CIausiusa-Masottiego podające zależność między makroskopową przenikalnością dielektryczną e a współczynnikiem polaryzacji deformacyjnej a.
Polaryzacja deformacyjna molowa Pd jest sumą polaryzacji atomowej molowej Pa i polaryzacji elektronowej molowej Pe
|
Pd = Pe + Pa |
= |
e - 1
e + 2 |
• |
Mc
d |
= |
4
3 |
p NL aa
| (2.12) |
gdzie NL - liczba Loschmidta.
Polaryzację elektronową Pe można obliczyć z wzoru Lorenza-Lorentza na refrakcję molową. Wykonując pomiar współczynnika załamania światła można obliczyć refrakcję molową RM i współczynnik polaryzacji elektronowej ae
Po podstawieniu wartości ae do wzoru (2.11) otrzymamy
|
RM |
= |
n2 - 1
n2 + 2 |
• |
Mc
d |
= |
4
3 |
p NL aa
| (2.13) |
gdzie n - współczynnik załamania światła.
Rodzaje i wartości energii oddziaływań międzycząsteczkowych podano na rys. 2.32.
2.5. Siły spójności
Wszystkie omówione rodzaje wiązań i oddziaływań międzycząsteczkowych (rys. 2.33) mogą być rozpatrywane jako siły spójności, czyli siły kohezyjne, w wyniku których z poszczególnych cząsteczek (czy atomów) tworzą się ciała o różnych stanach skupienia i różnych własnościach.
W tabl. 2.7 podano energię różnych rodzajów wiązań. Im większa jest energia wiązania, tym bardziej spójne jest dane ciało i trudniej go rozdrobnić, stopić lub przeprowadzić w stan gazowy.
Jak widać z rys. 2.33 jedynym typem wiązania o charakterze nieelektrostatycznym jest wiązanie kowalencyjne (atomowe), które jest wiązaniem kierunkowym o bardzo dużej energii wiązania. Pozostałe typy wiązań mają charakter niekierunkowy.
|
Tablica 2.7. Wartości energii różnych rodzajów wiązań pomiędzy cząsteczkami | |
Rodzaj wiązań | kJ/mol | |
Wiązania kowalencyjne | 418-628 | |
Wiązania jonowe i metaliczne | 209-418 | |
Wiązania wodorowe | 29,9-33,49 | |
Wiązania Van der Waalsa | 4,18-8,37 | |
- siły dyspersyjne | 0,837-8,37 | |
- siły elektrostatyczne (pomiędzy dipolami trwałymi) | do 8,37 | |
- siły indukcyjne | do 2,09
|
Największą spójność mają ciała stałe, w których siłami spójności są wiązania kowalencyjne. Przykładami substancji o wiązaniach wyłącznie kowalencyjnych są: diament C, krzem Si i węglik krzemu SiC (karborund). W strukturze diamentu każdy atom węgla jest tetraedrycznie otoczony przez cztery inne atomy, przy czym atomy wiążą się ze sobą poprzez wspólne pary elektronów (rys. 2.34).
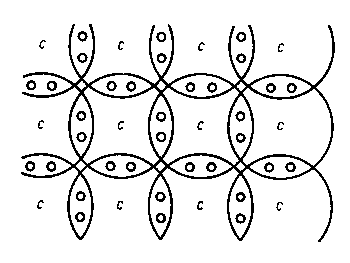 |
Rys. 2.34. Wiązanie cząsteczek diamentu mostkami elektronowymi
|
Wiązania atomowe w krysztale diamentu są kierunkowe i skierowane od środka do naroży regularnego czworościanu. W kryształach atomowych traci sens pojęcie cząsteczki chemicznej, gdyż nie można tu wyróżnić indywidualnych cząsteczek, lecz cały kryształ można uważać za jedną olbrzymią cząsteczkę.
Zależność twardości i temperatury topnienia kryształów atomowych od odległości międzyatomowej podano w tabl. 2.8. Jak widać z danych w tablicy wraz ze zmniejszeniem się odległości międzyatomowych
|
Tablica 2.8. Zależność trwalości ciał stałych od ich temperatury topnienia | |
Kryształ | Odległość
między atomami
nm | Twardość
w skali Mohsa | Temperatura topnienia
°C | |
C-C | 0,154 | 10,0 | 3500 | |
C-Si | 0,189 | 9,5 | 2700 | |
Si-Si | 0,235 | 7,0 | 1420 | |
Ge-Ge | 0,243 | 6,0 | 958
|
zwiększa się twardość i temperatura topnienia. Kryształy atomowe o ile nie zawierają domieszek i nie wykazują defektów sieciowych są dobrymi izolatorami i nie przewodzą prądu elektrycznego również i w stanie stopionym, gdyż nie tworzą jonów. Podobnie jak kryształy o wiązaniu atomowym wysoką energią kohezji odznaczają się kryształy o wiązaniu jonowym. Każdy taki kryształ możemy uważać za jedną olbrzymią cząsteczkę. W kryształach o budowie jonowej tworzące je jony starają się ułożyć jak najściślej obok siebie, aby zajmować jak najmniej miejsca w przestrzeni (zasada najściślejszego ułożenia kuł). Ułożenie jonów zależy od wielkości kationu i anionu. Według reguły Magnusa dla danego związku chemicznego struktura, a zatem i rodzaj wielościanów koordynacyjnych, zależne są od wzajemnego stosunku promienia kationu (rk) do promienia anionu (ra). Im kation jest mniejszy w stosunku do anionu, tym mniejsza jest liczba koordynacyjna kationu. Od reguły Magnusa istnieją odchylenia spowodowane głównie polaryzacją jonową, to jest działaniem deformacyjny m jednych jonów na drugie. Ze względu na wysokie wartości energii kohezji jonowej kryształy jonowe mają dużą twardość i charakteryzują się wysokimi temperaturami topnienia.
Przy danej strukturze twardość i temperatura topnienia są tym wyższe, im wyższa jest wartościowość jonów i im mniejsze są ich promienie (silniejsze wzajemne przyciąganie).
Miarą trwałości sieci krystalicznej jest energia sieci krystalicznej, tj. energia niezbędna do przeniesienia jonów z jednego mola substancji krystalicznej do nieskończoności.
W metalach siłami spójności są siły wiązania metalicznego, których energia wiązania ma wartość zbliżoną do energii wiązania jonowego. Każdy kryształ metalu można uważać za jedną olbrzymią cząsteczkę. Istnieje w nich tendencja do jak najściślejszego upakowania zrębów atomowych. Im ściślejsze jest upakowanie, tym większe są siły spójności. Siły te różnią się bardzo znacznie w zależności od rodzaju metalu, o czym świadczą różnice w twardości, temperaturze topnienia (rtęć -39°C, wolfram 3370°C), temperaturze wrzenia oraz wartościach współczynników rozszerzalności cieplnej i ściśliwości. Dla metali alkalicznych zależność między odległością międzyatomową a wspomnianymi własnościami przedstawiono w tabl. 2.9.
|
Tablica 2.8. Własności fizyczne metali alkalicznych | |
Metal | Li | Na | K | Rb | Cs | |
Odległość międzyatomowa, nm | 0,304 | 0,372 | 0,462 | 0,487 | 0,524 | |
Temperatura topnienia, °C | 179 | 97,7 | 63,5 | 30 | 28,5 | |
Temperatura wrzenia, °C | 1372 | 883 | 776 | 713 | 690 | |
Twardość, HB | - | 0,07 | 0,04 | 0,022 | 0,015 | |
Współczynnik rozszerzalności, a • 10 -6 | 58 | 71 | 84 | 90 | 97 | |
Współczynnik ściśliwości, b • 10 -6 | 8,6 | 14,2 | 23,2 | 32,8 | 34,6
|
Większej odległości między atomami, czyli mniejszej energii spójności odpowiadają mniejsze wartości współczynnika rozszerzalności cieplnej oraz ściśliwości. Z siłami spójności jest również związana charakterystyczna dla metali zdolność do deformacji plastycznej. W sieci metalicznej przesunięcie wzajemne sieci płaskich nie powoduje zmiany swobodnego ruchu elektronów ani zniszczenia wiązania. W przypadku kryształów o wiązaniu atomowym przesunięcie wzajemne płaszczyzn sieciowych powoduje zerwanie wiązań kierunkowych. W kryształach jonowych przesunięcie to może doprowadzić do zetknięcia się jonów ujemnych z ujemnymi i dodatnich z dodatnimi, przez co sieć przestaje być trwała na skutek wzajemnego odpychania jonów jednakowego znaku.
Duża liczba ciał stałych jest zbudowana z cząsteczek, między którymi jako siły spójności występują siły Van der Waalsa. Większość związków organicznych jest właśnie zbudowana w ten sposób. Spośród substancji nieorganicznych liczne pierwiastki chemiczne oraz związki, które pod zwykłym ciśnieniem i w pokojowej temperaturze występują w stanie gazowym lub ciekłym, mają po zestaleniu sieci cząsteczkowe (np. N2, O2, F2, Cl2, Br2, J2, He, CO2, SiF4 itd.) Substancje o strukturze cząsteczkowej w odróżnieniu od kryształów jonowych i atomowych mają niskie punkty topnienia i wrzenia, małą twardość oraz niezbyt dużą masę właściwą, gdyż odległości pomiędzy cząsteczkami są duże.
Siły międzycząsteczkowe zwiększają się wraz ze wzrostem ciśnienia (im bliżej siebie znajdują się cząsteczki, tym silniej się przyciągają). Wzrost temperatury powoduje przeciwny efekt niż siły przyciągania, gdyż wskutek ruchów cieplnych zwiększa się stan nieuporządkowania cząsteczek. Przy dostatecznie niskiej temperaturze nawet nieznaczne siły międzycząsteczkowe utrzymują cząsteczki w stanie ciekłym lub stałym. Wzrost ciśnienia powoduje podwyższenie temperatury wrzenia substancji, gdyż cząsteczki silniej się przyciągają.
W substancjach stałych o sieciach cząsteczkowych zazwyczaj występuje kilka rodzajów sił międzycząsteczkowych równocześnie, przy czym udział w siłach spójności różnych substancji jest różny. W każdym przypadku udział biorą siły dyspersyjne (Londona). W kryształach zestalonych gazów szlachetnych jako siły wiążące poszczególne cząsteczki ze sobą występują jedynie siły dyspersyjne. Siły dyspersyjne i konformacyjne spełniają również główną rolę jako siły spójności w kryształach niepolarnych węglowodorów oraz w przypadku związków wielkocząsteczkowych (polietylen, kauczuk). W substancjach, w skład których wchodzą cząsteczki polarne, znacznie większą rolę niż siły dyspersyjne spełniają siły orientacyjne (Keesoma) i indukcyjne (Debye'a).
Znacznie mniejsze siły spójności w porównaniu z ciałami stałymi występują w cieczach. W wyniku oddziaływania sił spójności cząsteczek sąsiadujących występują uprzywilejowane ukierunkowania, które jednak nie mogą objąć większego obszaru cieczy i ponadto nie mogą trwać długo. Takie ukierunkowanie ugrupowania cząsteczek (ciekłe kryształy) zostają rozpraszane przez ruchy termiczne. Obecnie nie ma jeszcze opracowanej zadowalającej teorii stanu ciekłego.
Teoria taka wychodząc z zależności pomiędzy składowymi cząsteczkami cieczy powinna wyrazić jej makroskopowe własności (lepkość, temperaturę wrzenia i krzepnięcia, rozpuszczalność itp.) oraz dać przesłanki do skonstruowania modelu stanu ciekłego i jego matematycznego opisu. W chwili obecnej istnieją trzy poważniejsze modele ciała ciekłego.
W modelu cieczy H. Eyringa, gdy usunie się z ciała stałego w przybliżeniu co ósmą cząsteczkę, a pozostałe cząsteczki wprawi się w szybki ruch, wówczas otrzyma się „gaz" złożony z luk rozproszonych w ciele stałym o wymiarach z grubsza odpowiadającym wymiarom cząsteczek, to znaczy otrzyma się „ciecz". Powyższe założenia są punktem wyjścia do tzw. modelu płynnych luk Eyringa.
W modelu cieczy J. Hildenbranda zakłada się w cieczy stan maksymalnego nieuporządkowania cząsteczek, zwłaszcza brak jakiegokolwiek uporządkowania dalekiego zasięgu poza pewnym porządkiem uwarunkowanym gęstością cieczy oraz wynikającym z zasady, że dwie cząsteczki nigdy nie mogą równocześnie zajmować tego samego miejsca w przestrzeni.
W modelu cieczy S. Rice wychodzi się z przybliżonego sposobu opisu matematycznego oddziaływań między parami i większymi grupami cząsteczek i stara się obliczyć najważniejszą funkcję dystrybucyjną, tzn. stosunek średniej gęstości cząsteczek \v pewnej odległości od dowolnej cząsteczki do całkowitej gęstości cieczy. Uważa on, że na tej podstawie można przewidywać makroskopowe własności cieczy.
Każdy z przedstawionych tu modeli cieczy ma poważne (choć ograniczone) zalety w tłumaczeniu makroskopowych własności cieczy. Niezależnie od prób opracowania modelu stanu ciekłego, nagromadziło się dużo materiału eksperymentalnego, na podstawie którego można ustalić wiele prawidłowości dotyczących tego stanu. Wiadomo np., że temperatura wrzenia wzrasta wraz ze wzrostem masy cząsteczkowej, gdyż im większe są cząsteczki, tym większe występują siły dyspersyjne. Ze względu na addytywność sił dyspersyjnych można ustalić prawidłowość we wzroście temperatury wrzenia dla szeregów homologicznych. Addytywność sił dyspersyjnych jest również przyczyną rozkładu cieplnego substancji składających się z dużych łańcuchowych cząsteczek (powyżej 70 atomów C). Siły przyciągania są tu tak duże, że cząsteczki nie mogą przejść w stan gazowy i wcześniej nim zostaną pokonane siły spójności zostają zerwane niektóre wiązania walencyjne, co wiąże się z rozkładem cieplnym substancji. Spośród związków łańcuchowych najwyższą temperaturę wrzenia mają związki o łańcuchu normalnym, natomiast rozgałęzienie łańcucha powoduje zmniejszenie powierzchni styku, a więc i obniżenie temperatury wrzenia. W podobny sposób można również tłumaczyć różnice w temperaturach topnienia, asocjacji cieczy, rozpuszczalności, lepkości i napięcia powierzchniowego, a więc różnice własności cieczy związane z siłami spójności.
2.6. Powierzchnia ciał stałych i ciekłych
2.6.1. Powierzchnia
Powierzchnią ciała nazywa się granicę rozdziału dwu faz, na której następuje skokowa zmiana własności jednej fazy na własności drugiej fazy. Jeżeli ciało nie znajduje się w próżni, to zawsze powierzchnia ciała jest powierzchnią międzyfazową. Rozróżnia się następujące powierzchnie międzyfazowe: ciecz-gaz, ciecz-ciecz, ciecz-ciało stałe, ciało stałe-gaz i ciało stałe-ciało stałe.
Powierzchnie graniczne istnieją tylko wtedy, gdy elementy składowe danego ciała (atomy, cząsteczki) są powiązane między sobą odpowiednio dużymi siłami spójności. W przeciwnym przypadku dochodzi do rozproszenia jednej substancji w drugiej. Z termodynamicznego punktu widzenia trwała powierzchnia międzyfazową występuje wtedy, gdy termodynamiczny potencjał jej tworzenia ma wartość dodatnią, natomiast w przypadku wartości zerowej i ujemnej istnieje tendencja do wzajemnego przenikania się faz.
Często spotykamy się z tendencją utożsamiania powierzchni fizycznej, a więc powierzchni ciała materialnego, z powierzchnią w sensie geometrycznym. Powierzchnia geometryczna jest tworem dwuwymiarowym, natomiast powierzchnia fizyczna jako twór materialny jest trójwymiarowa, pomimo że trzeci wymiar - grubość - jest względnie mały. Wiele zjawisk trybologicznych nie daje się naukowo wyjaśnić bez przyjęcia trójwymiarowości fizycznej powierzchni ciał.
Elementy budowy ciała (atomy, cząsteczki, jony) tworzące jego powierzchnię znajdują się w innych warunkach niż te elementy znajdujące się wewnątrz, gdyż od jednej strony powierzchni rozdziału otaczają je elementy innej fazy, oddziaływające na nie z innymi siłami niż elementy własnej fazy (rys. 2.35). W dalszych rozważaniach elementy budowy ciała będą rozpatrywane jako cząsteczki lub atomy.
W przypadku powierzchni rozdziału ciecz-gaz lub ciało stałe-gaz od strony fazy gazowej na cząsteczki powierzchniowe działają znacznie mniejsze siły
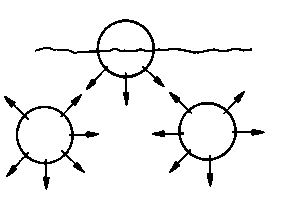
Rys. 2.35. Siły działające na cząsteczki znajdujące się wewnątrz ciała i na jego powierzchni |
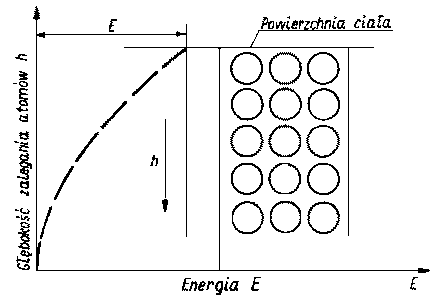
Rys. 2.36. Udział energii atomów warstwy przypowierzchniowej w całkowitej energii powierzchni
|
niż od strony własnej fazy. W rezultacie tego cząsteczki powierzchniowe mają część sił nieskompensowaną i powierzchnia jest bogatsza w energię niż wnętrze ciała.
Na cząsteczki warstwy powierzchniowej oddziałuje nie tylko pole sił cząsteczek warstwy leżącej w bezpośredniej styczności, ale również pole sił cząsteczek leżących głębiej. Oddziaływanie to zmniejsza się szybko wraz z głębokością „zanurzenia" się w materiał (rys. 2.36).
Występujące na powierzchni pole niewysyconych sił jest źródłem bardzo wielu zjawisk powierzchniowych. W przypadku powierzchni ciał stałych, a więc powierzchni, na których atomy powierzchniowe mają znacznie ograniczoną swobodę ruchu, nie jest obojętne z punktu widzenia wysycenia sił spójności, w jakim stopniu atomy powierzchniowe są otoczone innymi atomami. Jak wynika z rys. 2.37 inny jest stopień wysycenia sił atomu leżącego na powierzchni płaskiej, inny na
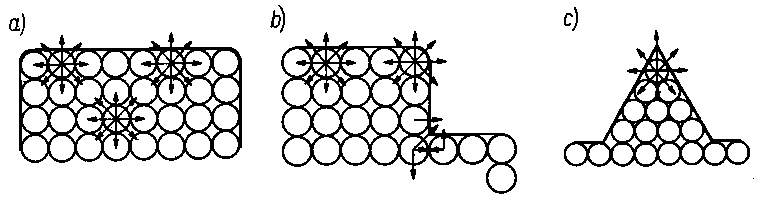 |
Rys. 2.37. Wpływ chropowatości na pole sił różnych powierzchni (a, b, c) elektronowymi
|
krawędzi, a jeszcze inny na narożu kryształu. W im mniejszym stopniu atomy powierzchniowe są otoczone innymi atomami, tym jest mniejszy stopień wysycenia sił, a więc większa energia powierzchniowa tych atomów.
Zatem zrozumiałe jest, że krawędzie ziarn kryształów są bogatsze energetycznie niż ich powierzchnie płaskie. Objawia się to większą reaktywnością atomów leżących na granicy ziarn (np. korozja międzykrystaliczna). Podobne efekty dają wszelkiego rodzaju naprężenia i defekty w strukturze siatki krystalicznej (rys. 2.38 i 2.39).
 |
Rys. 2.38. Model krawędzi krystalitów ciała stałego
|
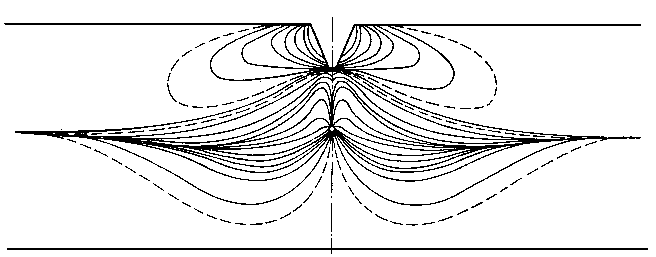 |
Rys. 2.39. Wpływ pęknięć na stan naprężeń w ciele stałym
|
W przypadku, gdy elementy budowy ciała (atomy, jony, cząsteczki) mają możliwość swobodnego poruszania się, jak np. w cieczy, to ciało dąży do zmniejszenia powierzchni (tj. obszaru bogatszego w energię), gdyż wtedy układ może osiągnąć minimum energii. Jest to zgodne z ogólnymi tendencjami w przyrodzie. Zmniejszenie powierzchni jest wynikiem działania na cząsteczki położone w warstwie powierzchniowej sił pochodzących od cząsteczek położonych głębiej. Wypadkowa tych sił jest skierowana do wewnątrz cieczy i dąży do wciągnięcia cząsteczek do cieczy. Powstające w ten sposób napięcie na powierzchni cieczy jest zwane napięciem powierzchniowym s, gdyż powierzchnia cieczy zachowuje się jak sprężysta błona. Napięcie w takiej błonie powierzchniowej jest stosunkiem sił stycznych do powierzchni cieczy i długości jej przekroju. Stąd ma ono wymiar niuton/metr.
Ze względu na to, że nad powierzchnią cieczy znajdują się cząsteczki jej pary, które oddziałują przyciągające na cząsteczki powierzchniowe cieczy, napięcie powierzchniowe s jest proporcjonalne do różnicy gęstości cieczy dc i gęstości pary dp
|
s = c |
( |
dc - dp |
)4
| (2.14) |
|
s ¼ |
= c |
( |
dc - dp |
)
| (2.15) |
gdzie c - stała.
Nad cieczą o niskiej prężności pary jest mało cząsteczek pary, dlatego też jest małe ich oddziaływanie. Przy dużej liczbie cząsteczek pary oddziaływanie jest silne.
Sudgen (w 1924 r.) pomnożył powyżej podany wzór na napięcie powierzchniowe przez masę cząsteczkową M^ i otrzymał wielkość, którą nazwał parachorą P
Przy małej prężności par można opuścić we wzorze gęstość pary dp i wtedy parachora jest wprost proporcjonalna do objętości molowej Vmol = Mc/dcWzór na parachorę ma postać
Parachora jest wielkością addytywną i konstytutywną. Addytywną jest dlatego, że można ją obliczyć sumując udziały (inkrementy), jakie mają w parachorze różne rodzaje atomów wiązań i pierścieni. Wartości inkrementów są obliczane i zebrane w specjalnych tablicach.
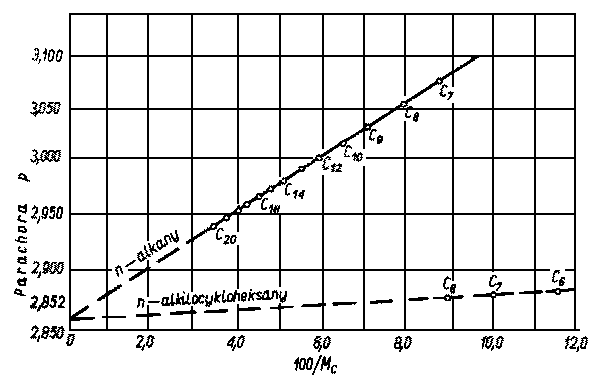 |
Rys. 2.40. Wartości parachory dla szeregów homologicznych węglowodorów; Mc - masa cząsteczkowa
|
Parachora jest również wielkością konstytutywną, gdyż jest ściśle związana z budową chemiczną cieczy. Na rys. 2.40 przedstawiono zależność parachory od masy cząsteczkowej i rodzaju węglowodorów. Tak więc parachora jest wielkością wiążącą budowę chemiczną cieczy z jej własnościami powierzchniowymi.
2.6.2. Własności energetyczne powierzchni
Każde ciało ma pewien zasób energii. Jeżeli pominie się energię, którą ciało ma w wyniku swego ruchu (kinetyczną) oraz położenia (potencjalną), a więc energię nie związaną ze strukturą ciała, to rozpatrując energię ciała związaną z jej strukturą można wyróżnić energię wewnętrzną i energię powierzchniową.
Energia wewnętrzna jest to całkowity zasób energii zmagazynowany we wnętrzu ciała. Należy wliczyć tu energię ruchów postępowych i rotacyjnych cząsteczek, wewnątrzcząsteczkowych drgań atomów, energię stanów elektronowych i jąder atomowych oraz wszystkie inne rodzaje energii występujące wewnątrz ciała. Dotychczas nie jest znana żadna metoda umożliwiająca stwierdzenie absolutnej wartości energii wewnętrznej, znane są tylko jej zmiany, na podstawie których oblicza się zmiany różnych funkcji termodynamicznych.
Energia powierzchniowa jest to różnica pomiędzy całkowitą energią wszystkich atomów lub cząsteczek warstwy powierzchniowej a energią, którą by one miały znajdując się we wnętrzu ciała (rys. 2.41). Miarą energii powierzchniowej
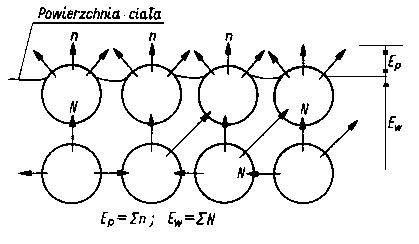
Rys. 2.41. Model rozkładu energii wewnętrznej Ew i energii powierzchniowej Ep |
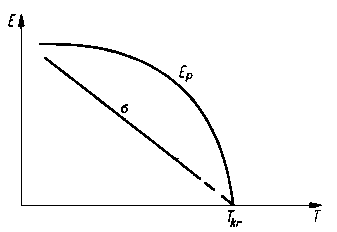
Rys. 2.42. Zależność napięcia powierzchniowego s i energii powierzchniowej Ep od temperatury T
|
jest praca, którą trzeba wykonać, aby przenieść atomy lub cząsteczki z wnętrza ciała na jego powierzchnię. Energia powierzchniowa w stanie krytycznym (tj. przy ciśnieniu i temperaturze krytycznej) równa się zeru, gdyż zanika różnica między fazami, a więc zanika i powierzchnia. W niektórych podręcznikach definiuje się energię powierzchniową jako energię atomów lub cząsteczek w warstwie powierzchniowej.
Takie sformułowanie jest błędne, gdyż energia atomów warstwy powierzchniowej rośnie wraz ze wzrostem temperatury, a energia powierzchniowa Ep maleje i w temperaturze krytycznej ma wartość równą zeru (rys. 2.42).
Podobnie jak energia powierzchniowa Ep wraz ze wzrostem temperatury maleje i napięcie powierzchniowe s, które w temperaturze krytycznej osiąga również wartość równą zeru. Zależność wartości napięcia powierzchniowego od temperatury podaje wzór Etvösa
|
sT = |
so a (Tk - T - 6 )
| (2.18) |
gdzie: a - wartość stała, Tk- temperatura krytyczna, so - napięcie powierzchniowe w temperaturze odniesienia, T - rozpatrywana temperatura.
Przy omawianiu własności energetycznych powierzchni nie można pominąć termodynamicznych aspektów tego zagadnienia. Z I zasady termodynamiki wynika zależność między energią układu U, ilością pobranego lub oddanego do otoczenia przez układ ciepła Q oraz ilością wykonanej lub pobranej przez układ pracy zewnętrznej L. Zależność tę można przedstawić wzorem
Jeżeli tym układem jest powierzchnia, to zmiana jej energii powoduje wykonanie pracy przez powierzchnię oraz wymianę z otoczeniem pewnej ilości ciepła.
Z II zasady termodynamiki wynika, że jeżeli w procesie odwracalnym zostaje wymieniona z otoczeniem ilość ciepła dQ w temperaturze T, to wartość przyrostu funkcji termodynamicznej, zwanej entropią s, jest równa
Z danych wielkości, które są przydatne do opisania stanu energetycznego powierzchni, należy przypomnieć swobodną energię Es i potencjał termodynamiczny G. Obydwie te wielkości służą do określenia, w jakim stopniu stan danego układu różni się od jego stanu równowagi. Jeżeli proces przebiega izohorycznie (v = const) i izotermicznie (t = const), to posługujemy się w takim przypadku pojęciem energii swobodnej.
Energia swobodna molowa
oraz energia swobodna
|
d es = d U - T d s
| (2.22) |
przy czym gdy układ osiąga stan równowagi, to d es = 0.
Jeżeli proces jest procesem izotermiczno-izobarycznym (v, p = const), to charakteryzujemy go potencjałem termodynamicznym.
Potencjał termodynamiczny molowy
oraz potencjał termodynamiczny
gdzie H - entalpia molowa, h - entalpia.
Z powyższych równań można przejść do wzorów Gibbsa-Helmholtza
|
d u = d es + T d s
| (2.25) | |
d h = d g + T d s
| (2.26) |
Wzory te wyrażają zależność między przyrostami d u, d es i d s oraz d h, d g i d s, dla każdej skończonej przemiany termodynamicznej zachodzącej w układzie. Iloczyn T d s nazywa się energią związaną układu. Przedstawia on tę część energii wewnętrznej u lub entalpii h, którą układ wymienia w postaci ciepła z otoczeniem w przemianie izotermicznej i kwasistatycznej. Natomiast d es i d g odpowiadają tej części wewnętrznej lub entalpii, która w procesie izotermicznym i kwasistatycznym jest wymieniana w postaci pracy L.
Z wzorów Gibbsa-Helmholtza widać wyraźnie, że chcąc zwiększyć powierzchnię musimy do układu doprowadzić pewną porcję energii, z której część zużywa się na zwiększenie powierzchni (d es lub d g w zależności od rodzaju przemiany - izohoryczno-izotermicznej lub izobaryczno-izotermicznej), a część zostaje związana przez układ w postaci ciepła (człon T d s).
Zastosujemy teraz podstawowe prawa termodynamiki do procesu zwiększania powierzchni:
- I zasada termodynamiki dla zwiększenia powierzchni o d A; układ pobiera ilość ciepła
|
d Q = d u + p d V - s d A
| (2.27) |
- II zasada termodynamiki; pochłonięcie ciepła d Q przy odwracalnym zwiększeniu powierzchni powoduje zmianę entropii układu
|
d u = T d s - p d V + s d A
| (2.28) | |
d es = -s d T - p d V + s d A
| (2.29) |
Dla układu otwartego, który może wymienić z otoczeniem zarówno energię, jak i ilość cząsteczek
|
d es = -s d T - p d V + s d A + | i = x
S
i = 1 | ui d Ni
| (2.30) |
gdzie : d Ni - liczba cząsteczek i-tego rodzaju w danej fazie.
2.6.3. Zależność między energią powierzchniową a napięciem powierzchniowym
W literaturze często energię powierzchniową utożsamia się z napięciem powierzchniowym. Często przeprowadza się rozumowania, które mają uzasadnić tę tożsamość. Poniżej zamieszczono tok rozumowania z jednego z podręczników.
Energia powierzchniowa i napięcie powierzchniowe są liczbowo i wymiarowo równe. Zagadnienie to można zilustrować następującym przykładem. Wyobraźmy sobie błonkę mydlaną rozpiętą na ramie drucianej, której jedna krawędź jest prze
 |
Rys. 2.43. Modelowa interpretacja napięcia powierzchniowego (ramka z drutu z błoną mydlaną)
|
suwalna (rys. 2.43). Odciągając krawędź ruchomą ramki o d x wykonujemy pracę d L, wbrew napięciu powierzchniowemu o wartości
W wyniku wykonania pracy d L powierzchnia błony zwiększyła się o d A, wobec tego wzrasta jej energia powierzchniowa, przy czym wzrost energii jest równy włożonej do układu pracy
-jest energią powierzchniową przypadającą na jednostkę powierzchni.
Ponieważ d A = l d x, więc z przedstawionych równań wynika, że
czyli napięcie powierzchniowe na jednostkę długości jest równe energii powierzchniowej na jednostkę powierzchni.
Powyższe rozważanie nie jest zgodne z przedstawionymi uprzednio obydwiema zasadami termodynamiki, a więc jest błędne (gdyż zakłada się, że wzrost energii powierzchniowej jest równy dostarczonej do układu pracy). Zgodnie z definicją energii swobodnej napięcie powierzchniowe jest swobodną energią przypadającą na jednostkę pola powierzchni. Wynika to jasno z przytoczonych uprzednio rozważań. Dodatkowo można podać dowód, który przeprowadził w swojej książce A. H. Cottrel (23). Przyjmuje on powierzchnię za silnik cieplny poddany obiegowi termodynamicznemu :
- przy rozciąganiu ciała w stałej temperaturze jego powierzchnia wzrasta o d A, energia o EPd A, wykonana praca jest równa s d A, a ciepło wchłonięte (EP - s) d A;
- ochłodzenie do temperatury T - d T - następuje przy stałej powierzchni (bez wykonania pracy);
|
- przy skurczeniu powierzchni o d A w stałej temperaturze d T jest wykonana praca
|
( |
s - |
d s
d T |
) |
d A ;
|
- ogrzanie do temperatury T odbywa się przy stałej powierzchni (bez wykonania pracy).
Zgodnie z podstawową teorią termodynamiki cykli odwracalnych stosunek przyrostu temperatury do temperatury jest równy stosunkowi pracy wykonanej przez układ podczas cyklu do ciepła wchłoniętego w wyższej temperaturze
|
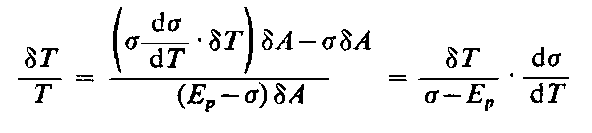
| (2.34) |
a stąd
Tylko w temperaturze 0 K. występuje zależność s = Ep. W temperaturach wyższych stosunek (d s/d T) jest ujemny, a s < Ep.
Ostatnie równanie można napisać w postaci
gdzie s - entropia powierzchni na jednostkę pola.
2.6.4. Sposoby wyznaczania napięcia powierzchniowego
Sposoby wyznaczania napięcia powierzchniowego opierają się na pomiarach wielkości związanych z napięciem powierzchniowym. Jeżeli pomiar jest tak prowadzony, że wszelkie wielkości potrzebne do określenia napięcia powierzchniowego są albo dane albo wyznaczane w czasie pomiaru, to w rezultacie przeprowadzenia pomiaru możemy obliczyć napięcie powierzchniowe.
Metoda wznoszenia cieczy w rurce kapilarnej
należy do statycznych metod pomiaru. Pomiar polega na zmierzeniu wysokości h, do której wznosi się ciecz w rurce kapilarnej o promieniu r (rys. 2.44). Ciężar słupa

Rys. 2.44. Pomiar napięcia powierzchniowego metodą wznoszenia cieczy w kapilarze Ep |
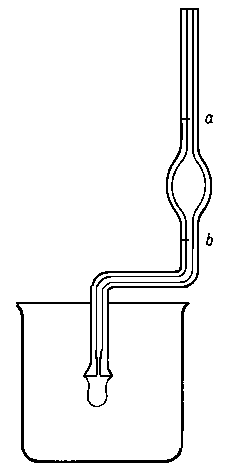
Rys. 2.45. Pomiar napięcia powierzchniowego metodą stalagmometryczną; a, b- poziom cieczy przed i po pomiarze
|
cieczy jest równoważony przez napięcie powierzchniowe. Zapisując to w postaci równania otrzymujemy
|
2 p r s = p r2 |
( |
h + |
r
3 |
) |
d g
| (2.38) |
gdzie: d - gęstość cieczy, g - przyspieszenie ziemskie, r/3 - poprawka na część cieczy zawartej w menisku.
Metoda stalagmometryczna określa napięcie powierzchniowe cieczy badanej w stosunku do napięcia powierzchniowego cieczy wzorcowej. Przyrządem służącym do pomiaru jest stalagmometr (rys. 2.45).
Jak widać z rysunku stalagmometr jest rurką wygiętą dwukrotnie pod kątem prostym, zaopatrzoną w kulisty pojemniczek na ciecz, o pojemności kilku cm3. Zakończony jest on szlifowaną stopką z otworkiem. Ciecz spływa ze stalagmometru kroplami, które tworzą się u wylotu otworka na stopce. Tworzące się krople zwiększają swoje wymiary dopóty, dopóki ciężar kropli nie zrównoważy siły napięcia powierzchniowego.
Pomiar prowadzi się dla cieczy badanej i dla cieczy wzorcowej (zwykle wody) o znanym napięciu powierzchniowym. Stosunek napięć powierzchniowych jest równy stosunkowi ciężarów kropel
Ze stalagmometru wypuszcza się ciecz o objętości zawartej między kreskami a i b (rys. 2.45) i liczy krople n, które utworzą się z objętości cieczy V
|
sx
swody |
= |
V dx g
nx |
: |
V dwody g
nwody |
= |
dx nwody
dwody nx
| (2.40) |
Metoda pęcherzykowa polega — na pomiarze ciśnienia, które jest niezbędne do przerwania przez pęcherzyk powietrza błony powierzchniowej cieczy. Urządzenie pomiarowe składa się z manometru wodnego 1 połączonego wężem 2 z kapilarą 3, która jest zanurzona w cieczy na głębokość h (rys. 2.46).
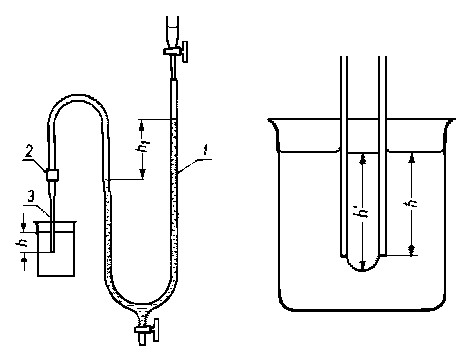
Rys. 2.46. Pomiar napięcia powierzchniowego metodą pęcherzykową
|
Ciśnienie manometryczne pm (mierzone słupkiem cieczy o wysokości h1), które jest potrzebne do przerwania błony powierzchniowej jest równe sumie ciśnienia hydrostatycznego ph, na poziomie h' i ciśnienia kapilarnego ps
|
pm = p'h + ps
| (2.41) | |
p'h = d h' g
| (2.42)
|
gdzie: d - gęstość cieczy, g - przyspieszenie ziemskie.
Ciśnienie kapilarne ps zależy od napięcia powierzchniowego s i od promienia pęcherzyka r
|
ps = |
2 r p s
r2 |
= |
2 r p s
r2 |
| (2.43) |
stąd
|
pm = d h' g + |
2 r p s
r
| (2.44) |
|
s = |
r
2 |
( |
pm - d h' g |
)
| (2.45) |
h' można podstawić do wzoru h (długość zanurzonej części kapilary).
Metoda tensometryczna
polega na pomiarze siły potrzebnej do oderwania od powierzchni cieczy pierścienia z cienkiego drutu platynowego. Jest to metoda szybka, prosta i dosyć dokładna. Do pomiaru siły potrzebnej do oderwania pierścienia stosuje się w dokładnych pomiarach wagi analityczne, przy wymaganej mniejszej dokładności - wagi skrętne. W metodzie tej trzeba uwzględnić poprawki na wiele efektów ubocznych (rys. 2.47).
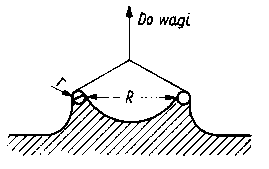
Rys. 2.47. Pomiar napięcia powierzchniowego metodą tensometryczna
|
Metoda Wilhelmy'ego polega na pomiarze siły potrzebnej do oderwania od cieczy płytki platynowej lub szklanej (grubość szkiełka przedmiotowego mikroskopwego). Siłę potrzebną do oderwania mierzy się za pomocą wagi.
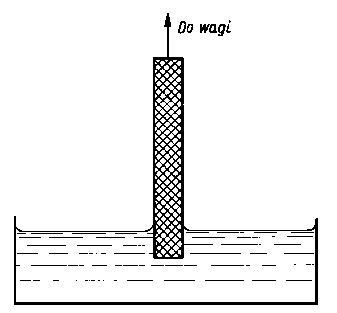
Rys. 2.48. Pomiar napięcia powierzchniowego metodą Wilhelmy'ego |
Rys. 2.49. Pomiar napięcia powierzchniowego metodą ważenia kropli
|
Jeżeli grubość płytki wynosi b, to napięcie powierzchniowe s można obliczyć ze wzoru na siłę Ge, która jest potrzebna do wyciągnięcia płytki z cieczy
gdzie Gp - ciężar płytki (rys. 2.48).
Metoda ta jest dokładna. Zgodność pomiarów z wynikami teoretycznymi wynosi około 0,1%. Nie jest wymagane stosowanie poprawek.
Metoda ważenia kropli
jest wygodną i szybką metodą oznaczania napięcia powierzchniowego polegającą na ważeniu kropli zbieranych do naczynia. Metoda opiera się na założeniu, że ciężar kropli G jest równoważony przez napięcie powierzchniowe s. Tate podał wzór wiążący ciężar kropli z napięciem powierzchniowym
gdzie r - promień rurki kapilarnej (rys. 2.49).
Przy tej metodzie jest wymagane stosowanie poprawek dla wyeliminowania wpływu różnych czynników zakłócających dokładność pomiaru.
|