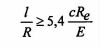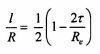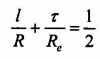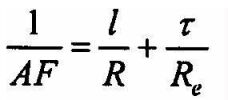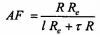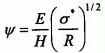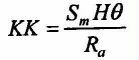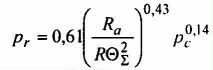l50lz

zużywanie tarciowe,
identyfikacja,
trwałość, obliczenia

Wiesław ZWIERZYCKI*

ZAGADNIENIA IDENTYFIKACJI PROCESÓW ZUŻYWANIA W STYKU TARCIOWYM

W referacie przedstawiono ogólną ocenę możliwości metod obliczeniowych w zakresie: wyznaczania naprężeń stykowych, identyfikacji wiodących procesów zużycia, określania intensywności zużywania i trwałości węzła.

* Instytut Maszyn Roboczych i Pojazdów Samochodowych Politechniki Poznańskiej, ul. Piotrowo 3, 60-965 Poznań.

l. WPROWADZENIE

Zużycie par tarciowych, szczególnie pracujących w trudnych warunkach (zapylenie, zawilgocenie, aktywność chemiczna środowiska), jest dominującą przyczyną utraty zdatności maszyn i pojazdów. Pomimo wielu prac tribologicznych trudno uznać problem sterowania trwałością (niezawodnością) węzłów kinematycznych (i innych elementów tribologicznych) za opanowany. Tak jak w przypadku innych elementów maszyn, pożądane jest przewidywanie przebiegu procesów zużyciowych już w fazie projektowania. Jest to szczególnie istotne w przypadku projektowania dużych obiektów wytwarzanych w skali jednostkowej. Dla takich przypadków rozwój wyrobu na podstawie doświadczeń wyłącznie eksploatacyjnych nie jest efektywny.

Problem „identyfikacji procesów zużywania” autor tego artykułu starał się umieścić w szerszym problemie prognozowania trwałościowo-niezawodnościowych parametrów układów tribologicznych. Osiągnięcie bowiem zużycia (luzu) granicznego jest w modelu niezawodnościowym traktowane jako utrata zdatności elementu (obiektu nieodnawialnego), przejście ze stanów dopuszczalnych do obszaru stanów niedopuszczalnych. Czas, w którym taki stan zostanie osiągnięty (trwałość węzła), zależy od intensywności (szybkości) zużywania elementów pary tarciowej. Zależy to od mechanizmu zjawisk stykowych. Powszechnie uważa się, że dla węzłów, w których nie jest możliwe uzyskanie warunków tarcia płynnego, względnie dobrą trwałość i stabilny przebieg procesu zapewnia tzw. zużywanie utleniające (mechanochemiczne przez utlenianie [l]). Według innej szkoły [2] takie warunki zachodzą w styku sprężystym dotartym.

Poniżej scharakteryzowano stan wiedzy teoretycznej o możliwości modelowania zjawisk stykowych, szczególnie w aspekcie opisu zużywania podczas tarcia.

2. MODELE MIKRO-1 MAKROMECHANICZNE W UKŁADACH STYKOWYCH

Przy obliczaniu stykowych charakterystyk powierzchni chropowatych (rzeczywistej powierzchni styku, zbliżenia, rozmiarów mikrostyków, naprężeń w stykach elementarnych) wychodzi się zazwyczaj z modelu, w którym jedną z powierzchni przyjmuje się jako doskonale gładką, drugą- chropowatą. Chropowatość powierzchni modeluje się układem występów o jednakowej formie geometrycznej i zmiennej wysokości (opisanej stosownym rozkładem statystycznym). Od tego jaki założy się kształt wierzchołka chropowatości (walec, czasza kulista, stożek, stożek ścięty itp.) zależą charakterystyki geometryczne wykorzystywane w dalszych obliczeniach. Kolejny etap obliczeń polega na rozwiązaniu zagadnienia stykowego (na gruncie teorii sprężystości) dla pojedynczej nierówności. Przyjmuje się przy tym założenie, że względne przemieszczenie (zagłębienie) sztywnego występu modelującego pojedynczą nierówność chropowatości zależy od obciążenia, które na nią przypada. Konkretna postać takiej zależności jest zależna od kształtu geometrycznego nierówności. W ostatnim etapie obliczeń wykorzystuje się warunek równowagi stanowiący, że suma obciążeń przejmowanych przez mikrostyki jest równa sile ściskającej przyłożonej do układu. Stosuje się dwa podejścia: model (uproszczony) oddziaływania „izolowanego” występu z półprzestrzenią sprężystą oraz model rozwinięty, w którym uwzględnia się dodatkowo naprężenia pochodzące od sąsiednich nierówności.

Z analizy modeli mikromechanicznych, opisujących oddziaływania stykowe, przeprowadzonej w pracy [3] wynika, że:

1)

w styku statycznym (bez uwzględnienia tarcia):

-: popełnia się błąd w ocenie sztywności układu stykowego, jeśli zaniedbuje się wpływ sąsiadujących ze sobą nierówności wzajemnie na siebie. Posługując się modelem „izolowanego” występu otrzymujemy zawyżoną ocenę sztywności. Błąd jest tym większy im większa jest liczba występów i większa gęstość ich rozmieszczenia;
-: kształt elementarnego płaskiego obszaru styku (kołowy, eliptyczny, trójkątny) nie ma istotnego wpływu na ocenę sztywności układu stykowego;
-: modele mikromechaniczne umożliwiają dogłębną analizę procesu nawiązywania styku w przypadku zróżnicowanej wysokości układu występów powierzchni;

2)

w modelu z udziałem tarcia:

-: na rozkład naprężeń normalnych w strefie styku parabolicznego występu ze sprężystą półprzestrzenią nie wpływa składowa adhezyjna t_o , a jedynie piezowspółczynniki µ. (model t = t₀ - m s);
-: piezowspółczynnik µ (współczynnik tarcia z modelu Amontonsa) wpływa na asymetrię styku - strefa styku przesuwa się względem osi symetrii występu; przy obliczeniach układów rzeczywistych można wpływ tarcia na rozkład naprężeń normalnych w elementarnych stykach zaniedbać.

Mikromechaniczne opisy można wykorzystać również do analizy kinetycznej procesu docierania powierzchni chropowatych [4]. Wymaga to jednak przyjęcia określonego modelu matematycznego opisującego zużywanie.

Strefę styku dwóch ciał sprężystych można opisywać również za pomocą makroskopowych modeli teorii sprężystości. W odróżnieniu od modeli mikromechanicznych, strukturalnych nazywa się je modelami kontynualnymi. Na takim poziomie również rozważano wpływ chropowatości powierzchni na charakterystyki stykowe oraz wpływ tarcia i zużywania tarciowego. Szczegółową analizę tych modeli dla przykładowej pary jaką jest łożysko ślizgowe poprzeczne zamieszczono w pracach [3-8].

Ważniejsze wnioski, które wynikają z analizy tej grupy metod są następujące [3, 7j:

-: w większości metod traktuje się stykające się ze sobą walce (jeden wewnętrzny, drugi zewnętrzny) o promieniach prawie równych jako idealnie gładkie; dla względnie małych stref styku (półkąt strefy styku (p < 20°) rozkład naprężeń stykowych wyznaczyć można z metody Hertza, dla większych stref styku wprowadza ona znaczny błąd do oceny - wtedy można zastosować metody dokładniejsze, np. przedstawione w pracach [9, 10];
-: wpływ chropowatości na charakterystyki stykowe uwzględnia się wprowadzając do wzoru na całkowite zbliżenie ciał - składowej wynikającej z deformacji występów nierówności chropowatości;
-: tarcie (naprężenia styczne w modelu) wywołuje asymetrię rozkładu naprężeń normalnych, lecz w przypadku układów smarowanych (tarcie mieszane, graniczne) można jego wpływ pominąć;
-: w analizie nominalnych naprężeń stykowych należy w niektórych przypadkach uwzględnić wpływ warstw pośrednich;
-: zużycie elementów współpracujących w sposób istotny zmienia charakterystyki naprężeniowe styku (co z kolei wpływa na zmianę intensywności zużywania); w parze prostej rośnie strefa styku i „spłaszcza” się rozkład naprężeń normalnych, w parze ślizgowej odwróconej występuje zmniejszenie strefy styku i wzrost naprężeń maksymalnych; rozwiązywanie tego typu zagadnień wymaga również, jak w modelach mikromechanicznych, przyjęcia matematycznego modelu zużywania.

W przeanalizowanych metodach obliczeniowych posługiwano się modelem uproszczonym, w którym liniowa intensywność zużywania I_h, (stosunek zużycia liniowego h do drogi tarcia L) była wprost proporcjonalna do normalnych naprężeń stykowych p), czyli I_h = K • p (gdzie K- nazywane jest wskaźnikiem zużycia).

W dalszej części artykułu zamieszczono uwagi dotyczące matematycznych modeli zużywania, wcześniej jednak omówiono pomocnicze kryteria, przy pomocy których można w fazie obliczeniowej rozróżniać (identyfikować) rodzaje oddziaływań stykowych, prognozować mechanizmy zużywania i dobierać stosowne do nich modele matematyczne opisujące intensywność (szybkość) zużywania.

3. PRZEWIDYWANIE RODZAJÓW ODDZIAŁYWAŃ
(MECHANIZMÓW ZUŻYWANIA) W STYKACH ELEMENTARNYCH

Najbardziej rozpowszechnione, tradycyjne kryterium sprawdzające przydatność materiału do pracy w układzie ślizgowym przewiduje sprawdzenie warunku p Ł p_kr, i p v Ł (p v)_kr (czasem łącznie z kryterium v Ł v_kr). W pewnym przybliżeniu można uznać, że dla obciążeń mniejszych od krytycznych materiał będzie się zużywał w sposób ustabilizowany, dla wartości większych w sposób katastroficzny. Działania technologów warstw wierzchnich zmierzają do przesunięcia hiperboli p v = (p v)_kr maksymalnie w prawo. Szczegółowo to zagadnienie rozpatrzono w pracy [11].

Z kolei „rozszyfrowaniem” pola zużywania ustabilizowanego zajmowali się S.C. Lim i M.F. Ashby [12]. Analizując wyniki badań zużyciowych kilkudziesięciu autorów utworzyli doświadczalną, a następnie teoretyczną „mapę mechanizmów zużywania” (wear - mechanism map). W układzie „p - v” wskazano dla różnych par metalicznych (stalowych) obszary wymuszeń, w których występuje zacieranie (seizure), zacieranie termiczne (melt wear), zużywanie utleniające (oxidation wear) w wersji łagodnej (mild} i intensywnej (severe), delaminacyjne.

Ilościowe kryteria rozróżniające warunki w elementarnych obszarach styku tarciowego spotkać można w pracach LV. Kragielskiego [2, 13]. Między innymi do tego celu wykorzystywana jest geometryczna charakterystyka styku pojedynczej chropowatości l/R (gdzie /jest wielkością zagłębienia nierówności w kształcie czaszy kulistej o promieniu R) oraz tzw. czynnik fizykomechaniczny t/Re, gdzie t oznacza naprężenie ścinające w połączeniu tarciowym, a Re jest granicą plastyczności.

Za pomocą tych dwóch bezwymiarowych charakterystyk wyrażono tzw. punkty krytyczne, rozdzielające różne formy kontaktu:
- przejście od deformowania sprężystego do plastycznego podane jest warunkiem:

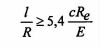(1)

gdzie c zmienia się w przedziale 3-6 w zależności od stopnia zgniotu, głębokości wnikania l i od tzw. czynnika skali.

- punkt krytyczny przejścia od deformacji plastycznej do mikroskrawania wyraża się zależnością:

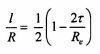(2)

którą można przekształcić do postaci:

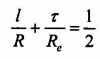(3)

Im bardziej suma tych bezwymiarowych charakterystyk różni się od 0,5, tym dalsze od mikroskrawania są warunki pracy węzła. Można zatem tę sumę uznać za liczbową charakterystykę, oceniającą zdolność do pracy (tj. do zachowania warunków tarcia zewnętrznego) skojarzenia tribologicznego. Odwrotność tego wyrażenia I. V. Kragielski nazwał „liczbą antyfrykcyjności” (w oryg. j. ros. - ćislo antifrikccionnosti)[13]:

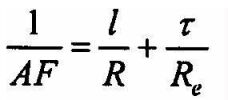(4)

więc

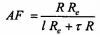(5)

Przy wartości AF = 2 zostaje przekroczony próg tarcia zewnętrznego (niszczenie więzi tarciowej następuje w obrębie materiału podstawowego). Adhezyjne niszczenie połączeń tarciowych leży w obrębie tarcia zewnętrznego (t/Re < 0,5), zaś odrywanie kohezyjne materiału (t/Re > 0,5) w obszarze tarcia wewnętrznego.

N.W. Gitis [14] przeprowadził eksperymenty, w których rejestrował zagłębienie l czaszy kulistej R przy tarciu o materiał z granicą plastyczności Re. Wytrzymałość „więzi” tarciowej wyznaczał ze wzoru:

t = (µ - µ_d) p_r (6)

gdzie µ to współczynnik tarcia wyznaczony eksperymentalnie, µ_d zaś jest jego składową deformacyjną (wyliczoną ze wzoru µ_d = 0,55 • sqrt(l/R), p_r naprężeniem rzeczywistym, tj. w styku elementowym (p_r = HB w warunkach styku plastycznego, HB - twardość materiału w stopniach Brinella). Uzyskane przez N.W. Gitisa krytyczne wartości liczby AF (oznaczające przejście z warunków tarcia zewnętrznego na tarcie wewnętrzne) podano w tabeli 1.

Z wyników przedstawionych w tabeli l widać, że wartości krytyczne AF zbliżone są do liczby 2. Oznacza to, że tarcie zewnętrzne ciał stałych nie jest możliwe poniżej AF_kryt. Dla łagodnych warunków styku, a więc przy odkształceniach sprężystych AF osiąga wartość ponad 100 dla stali, zaś ponad 10000 dla metali kolorowych [14]. Tabela l. Krytyczne wartości liczby „antyfrykcyjności” AF [14]

Materiał	Rodzaj obróbki cieplno-chemicznej	AF_kryt
stal 45	odpuszczanie wyżarzanie	1,98 2,07
stal 40H	wyżarzanie	1,80
stal 18HG	odpuszczanie hartowanie nawęglanie	1,84 1,69 1,55
mosiądz LS64-3	odpuszczanie	1,92
stal U 11A	normalizacja	1,74
stal 38HMJuA	odpuszczanie azotowanie	1,83 1,48
żeliwo SCz21-40	odpuszczanie	1,81

W innej wersji, (za W.S. Kombałowem [15]) można rodzaj styku (i idący za tym mechanizm zużywania) ocenić porównując wyliczone naprężenia rzeczywiste p_r z twardością materiału HB.

Jeśli

p_r < HB

(7)

to styk ma charakter sprężysty, bowiem styk plastyczny charakteryzuje najczęściej wartość naprężenia p_r » HB. Przybliżone metody obliczania p_r w różnych sytuacjach podano w tabeli 2.

Rozróżnienia między stykiem sprężystym i plastycznym w obszarach elementarnego styku można dokonać za pomocą, wprowadzonego przez J.A. Greenwooda i J.B.P. Wiliamsona [za 16] tzw. indeksu plastyczności:

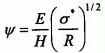(8)

gdzie: H - twardość powierzchni chropowatej, E - kompleksowa stała sprężystości układu obu ciał, s - odchylenie standardowe rozkładu wysokości chropowatości, R - średnia wartość promienia zaokrąglenia wierzchołka chropowatości. Przy wartości y < 0,6 styk ma charakter sprężysty, natomiast przy y > 1 występują wyłącznie oddziaływania plastyczne.

Należy jednak wziąć pod uwagę fakt, że wierzchołki chropowatości pozostające pierwotnie w styku plastycznym podczas docierania zmieniają swoją geometrię, co może doprowadzić do zmiany charakteru oddziaływania. Takie sytuacje opisuje kryterium sformułowane przez A.Ja. Komolsa [17] w postaci:

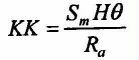(9)

Tabela 2. Przybliżone wzory na wartość naprężenia rzeczywistego [15]

Deformacja	Powierzchnie i naprężenia	Wzór obliczeniowy
sprężysta	dwie chropowate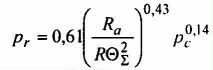
sprężysta	chropowata z gładką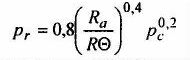
plastyczna	p_c Ł (1/3) HB	p_r » HB
plastyczna	p_c Ł (1/3) HB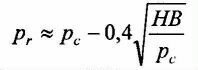
R=R₁ · R₂/(R₁ + R₂) ; Q = (1 - m²) E ; dla dwóch ciał deformowanych : Q = Q₁ + Q₂

Im wyższa jest wartość współczynnika KK, tym mniejsze naprężenie panuje w strefie styku i zużycie jest również mniejsze. Kryterium to dobrze charakteryzuje proces docierania [17]. Krytyczne wartości wskaźnika wynoszą: KK > 1,75 określa styk sprężysty, KK < 0,7 - styk plastyczny, zaś w przedziale od 0,7 do 1,75 ma miejsce styk sprężysto-plastyczny [17].

4. OBLICZANIE SZYBKOŚCI ZUŻYWANIA

Obszerną analizę formuł matematycznych wyrażających szybkość (intensywność) zużywania jako funkcję parametrów tarcia p i v zawierają prace [7, 8, 18, 19]. H.C. Meng i K.C. Ludema [18] doliczyli się aż 180 równań, w których sto zmiennych i stałych opisujących zużywanie przy tarciu ślizgowym. We wspomnianej pracy przeanalizowano również opisy matematyczne zużycia erozyjnego (28 różnych równań, łączna liczba cech wyniosła 33).

Korzystanie z tak wielu zmiennych w obliczeniach inżynierskich byłoby wysoce nieefektywne, istnieje zatem konieczność uproszczenia modeli wyrażających ilościowo zużycie. Wydaje się, że sensowne jest wykorzystanie do obliczeń szybkości zużywania v_z zależności:

v_z = Kp^x v (10)

w której stałe K i x są funkcjami własności materiałowych, charakterystyk geometrycznych powierzchni itp. Związki stałych K i x ze zmiennymi występującymi w różnych modelach teoretycznych wykazano głównie w pracy [8]. Otwarty pozostaje sposób pozyskiwania danych tribologicznych w postaci stałych K i x. Pewne przesłanki co do sposobu doświadczalnego wyznaczania tych stałych zawarto w pracy [3].

Model zużywania v_z = K p^x v jest elementem modelu opisującego trwałość węzła ślizgowego

T = (Z_o - Z_gr)/(K p^x v) (11)

gdzie: Z_o i Z_gr oznaczają luz początkowy i graniczny w skojarzeniu.

5. ZAKOŃCZENIE

Dużym ograniczeniem metod wywodzących się z teorii sprężystości, służących do oceny rozmiarów strefy styku, rozkładu w jej obrębie naprężeń normalnych, od której zależy intensywność zużywania, jest to, że są one możliwe do zastosowania tylko w przypadku styku elementów o prostych kształtach geometrycznych (np. w kształcie walca).

Bardziej uniwersalne, choć przybliżone podejście, zastosowano w pracy [3]. Opracowano algorytmy umożliwiające obliczeniową analizę zużywania się wybranych par tarciowych o różnej funkcji i strukturze, zastosowano metodę różnic skończonych; zużycie jako proces dyskretny analizowane jest w punktach węzłowych strefy styku tarciowego łożyska ślizgowego, przegubu wahliwego, przekładni zębatej oraz mechanizmu krzywkowego. Algorytmy te są elementami prototypowego systemu, którego zadaniem jest teoretyczna analiza niezawodnościowa elementów (par) maszyn podlegających zużywaniu.

[ l]: KOSTECKIl B.L, NATANSON M.E., BERŚADSKII L.I., Mechanochimićeskie processy pri trenu. Moskva, Nauka, 1972.
[ 2]: KRAGELSKI1 LV., Trenie i iznos w masinach. Moskva, Masinostroenie, 1968.
[ 3]: Fizyczne podstawy doboru materiałów na elementy maszyn współpracujące tarciowo. Pod red. W. Zwierzyckiego i M. Grądkowskiego. Radom, Wyd. ITeE, 2000.
[ 4]: GOR1AĆEVA I.G., DOBYĆIN M.N., Kontaktnye zadaci v tribologii. Moskva, Masinostroenie. 1988.
[ 5]: GOR1AĆEVA I.G., DOBYĆIN M.N., Teoreticeskie osnovy metoda rasceta zestkosti styka serochmatych tel s ućetom vzaimnogo vlijanija mikrokontaktov. Maśinovedenie, 1979, nr 6, s. 66-71.
[ 6]: GOR1AĆEVA I.G., DOBYĆIN M.N., Ocenka tocnosti metoda rasceta zestkosti styka serochovalych tel s ućetom vzaimnogo vlijanija mikrokontaktov. Masinovedenie, 1980, nr l, s. 70-71.
[ 7]: ZWIERZYCK1 W., Zagadnienia apriorycznej oceny trwałości węzłów tarcia ślizgowego. Poznań. Wyd. Politechniki Poznańskiej, 1990.
[ 8]: ZWIERZYCK1 W., Prognozowanie niezawodności zużywających się elementów maszyn. Radom. Wyd. ITeE, 1998.
[ 9]: GAFNER S.L., DOBYĆIN M.N., K rasćetu ugia kontakta pri vnutrennem soprikosnovenii cilindriceskich tel, radiusy kotorych pocti ravny. Masinostroenie, 1973, nr 2, s. 69-74.
[10]: USOV P.P., Opredelenie zony kontakta i kontaktnych naprjazenii pri vnutrennem soprikosnowmi cilindrićeskich tel. Maśinovedenie, 1981, nr 6, s. 75-81.
[11]: NOSAL S., Tribologiczne aspekty zacierania się węzłów ślizgowych. Poznań, Wydawnictwo Politechniki Poznańskiej, 1998.
[12]: LIMS.C., ASHBYM.F., Wear - mechanism maps. Acta Metallurgica, Vol. 35 1987. No l. p. 1-24.
[13]: KRAGELSKI.I I.V., O novoj charakteristike frikcionnogo soclenija - cislo antifrikcjonnosti. DAN SSSR, t. 193, nr 2, s. 320-322.
[14]: GITIS N.V., Vlijanie fiziko-mechanićeskich svojstv metallov na porog vnesnego trenija [w:] Problemy trenija i iznasivanija. Vyp. 22, Technika, Kiev 1982, s. 40-43.
[15]: KOMBALOV V.S., Ocenka tribotechniceskich svojstv kontaktirujuscich poverclmostej. Moskva. Nauka, 1983.
[16]: HUTCH1NGS I.M., Tribology: friction and wear of engineering materials. Ed. Edward Arnold. London, Melburne, Auckland, 1992.
[17]: KOMOLS A. Ja., Eksperimentalnye issledovanija osnovnych charakteristik kontaktirovanija poverchnostej trenija [w:] Mikrometrija i ekspluatacionnye svojstva masin, Riźskij Politechnićeskij Institut. Riga 1985, s. 32-39.
[18]: MENG H.C., LUDEMA K.C., Wear models and predictive equations: their form and content. Wear. vol. 181-183 (1995), p. 443-457.
[19]: SZCZEREK M., Klasyfikacja zużycia, podział zużycia ze względu na sposób przejawiania się i detekcji. Tribologia, 1999, nr 6, s. 187-194.

GENERAL APROACH TO THE PROBLEM OF WEAR PROCESSES IDENTIFICATION

In this paper the general evoluation the theretical methods in the field of:
- contact stresses calculation,
- the main wear mechanisms identification,
- the wear rate and durability prediction of friction pairs, were presented.