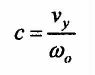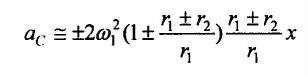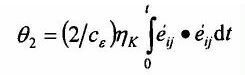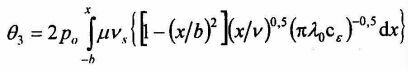| |
tarcie toczne, sprzężenie cierne, modelowanie
Czesław KOZIARSKI*
MODEL SPRZĘŻENIA W TARCIU TOCZNYM
Przedstawiono nowy model mechanizmu sprzężenia elementów tocznych uwzględniający poślizgi geometryczne, sprężyste oraz poślizgi wynikające z odkształceń plastycznych w miejscach rzeczywistego styku. Ponadto uwzględniono: różnice wartości współczynników tarcia kinematycznych i statycznych, poślizgi powodowane różnicą temperatury w polu styku elementów tocznych. Są w nim też uwzględnione siły bezwładności wywoływane nie tylko przemieszczeniami stycznymi, ale też powodowane odkształceniami promieniowymi, które wywołują dodatkowe przyspieszenia dośrodkowe oraz obwodowe nazywane przyspieszeniami Coriolisa.
* Politechnika Wrocławska, Instytut Konstrukcji i Eksploatacji Maszyn, ul. Łukasiewicza 7/9. 50-370 Wrocław.
l. MODEL SPRZĘŻENIA
Wychodząc z modelu Lutz'a [4], opracowano przedstawiony na rys. l model sprzężenia elementów tocznych. Wprowadzone do modelu pojęcie dewiacji punktu tocznego C oznaczono na osi x literą c, której wartość wynosi
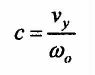 | (l) |
gdzie: wo - prędkość tarcia wiertnego, zaś prędkość poślizgu środka pola styku S wzdłuż osi y równa jest
|
vy = vv + f wo + v sin s | (2) |
w którym: vv - prędkość przemieszczania po sobie elementów tocznych wzdłuż linii ich styku, f- ramię tarcia tocznego, v- prędkość obwodowa środka pola styku, s - kąt wichrowatości osi elementów tocznych.
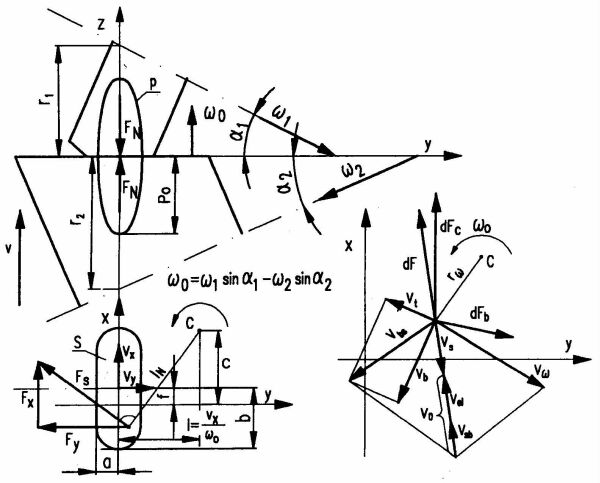Rys. l. Model sprzężenia elementów tocznych, gdzie: a - jedna druga długości pola styku S. którego połowę szerokości oznaczono jako b.
Fig. l. Model of the roling elements coupling, where a is one half of the length of the contact area S and b is one half of is width
|
Położenie punktu tocznego C na osi x określa wartość nazywaną oddaleniem l tego punktu. Jest ona proporcjonalna do składowej prędkości poślizgu geometrycznego w środku pola styku vx, wywoływanej wykorzystywaniem siły tarcia do przekazywania siły obwodowej Fx = vT F. Siła ta wraz z siłą do niej prostopadłą Fy = vv F składa się na siłę sprzężenia elementów tocznych Fs, która działając na ramieniu lN wywołuje moment tarcia wiertnego Mo = a vMo F. Bezwymiarowe współczynniki vT oraz vv są stopniami wykorzystania siły tarcia, a vMo, jest współczynnikiem momentu tarcia wiertnego. Zakładając powierzchniową sztywność bieżni elementów tocznych, siła ta wynosi F = µkin FNN, gdzie: µkin - kinematyczny średni współczynnik tarcia w polu styku, a FN - siła docisku elementów tocznych wywołująca nacisk p. Uwzględnienie powierzchniowej podatności prowadzi do dF = µkin p dS, gdy vs = vsum - vo > 0 oraz dF=µstat •p•dS•vsum/vo, kiedy vs = 0. Kinematyczny współczynnik tarcia µkin = f(p, v, oraz T), natomiast statyczny µstat=f(p i T), gdzie T - temperatura pracy w punkcie styku.
Według kinematycznego prawa tarcia [l], suma poślizgu geometrycznego vw = rw•wo, oraz poślizgu powodowanego różnicą przemieszczeń vbs jest zmniejszana o prędkość poślizgu odkształceniowego vo = y vel. Wyznaczany doświadczalnie współczynnik y jest wielokrotnością prędkości poślizgu sprężystego wywołanego elementarną siłą tarcia
|
vel = [4pµ(2 - n) n / (p G)] arcsh l, | (3) |
(gdzie: n - współczynnik Poissona a G - moduł sprężystości postaciowej) w stosunku do wartości rzeczywistej, czyli prędkości poślizgu odkształceniowego vo.
Prędkość vo dlatego jest większa niż wartość obliczona z zależności (3), bo w rzeczywistym miejscu styku zachodzi również odkształcenie plastyczne oraz postaciowe odkształcenie sprężyste. Zachodzi tam też pękanie kończące się często ubytkiem. Nie znamy sposobu analitycznego wyznaczania wartości tych odkształceń, uzyskano je jedynie dla założonego modelu dwóch stykających się nierówności i tylko z uwzględnieniem odkształceń sprężysto-plastycznych w [5]. Z przeprowadzonej w tej pracy analizy wynika, że przemieszczenia na rzeczywistych powierzchniach styku mogą być wielokrotnie większe od przemieszczeń obliczonych dla półprzestrzeni sprężystej. Potwierdzają to też prace doświadczalne prowadzone w tarciu ślizgowym. Poślizg wywołany innymi niż sprężyste odkształceniami, powstałymi wskutek działania elementarnej siły tarcia, oznaczono na rys. l jako nsb.
2. WPŁYW ODKSZTAŁCEŃ I OBCIĄŻEŃ CIEPLNYCH
Oprócz sił bezwładności wywoływanych przemieszczeniami stycznymi, które są oznaczone na rys. l jako dFb, w punkcie styku elementów tocznych działają też siły bezwładności oznaczone jako dFc wywoływane przemieszczeniami promieniowymi wywołują przyspieszenia, które według [2] wynosi
|
ar @ r2w22/[1 - x2/(r1 r2)] | (4) |
Zwiększa ono, w środku pola styku, wartość przyspieszenia dośrodkowego na kole 1 o wartość takiego przyspieszenia na kole 2. W polu styku elementów tocznych, których bieżnie wykonano z jednakowych materiałów, na przykład koła i szyny, dodatkowe przyspieszenie promieniowe w polu styku wynosi
|
ar @ -0,5 n2/ r = 0,5w2 r | (5) |
Zwiększa to w całym polu styku prawie półtorakrotnie przyspieszenie dośrodkowe, które wywołuje powierzchniowe siły odśrodkowe. Ma to istotny wpływ na rozkład i wartość nacisku p przy większych wartościach prędkości obwodowych v, przez zwiększanie krzywizny w miejscu styku elementów tocznych.
W ogólnym przypadku można przyjąć, z dużym przybliżeniem, że
|
ar1,2 @ (1 - E1,2) v2/r = (1 - E'1,2/E)w2r | (6) |
Przemieszczenia promieniowe wywołują też przyspieszenia w płaszczyźnie styku elementów tocznych, nazywane przyśpieszeniami Coriolisa, które według [2] wynoszą
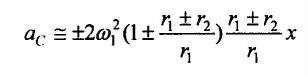 | (7) |
gdzie w nawiasach i ułamkach znaki górne obowiązują w przypadku styku zewnętrznego, a dolne dla styku wewnętrznego. Gdy promienie kół w punkcie ich styku r1 i r2 są jednakowe, to dla styku zewnętrznego przyśpieszenie Coriolisa aC=12w12 x jest porównywalne z przyspieszeniem dośrodkowym. Może więc ono istotnie wpływać na parametry sprzężenia szerokich pól styku. W polu styku koła i szyny wykonanych z jednakowych materiałów, przyspieszenie to wynosi
Analogicznie do przyspieszenia promieniowego można przyjąć ogólnie, że
|
ac @ -2(l- E'1,2/E)v2 x/r2 = -2(1 - E'1,2/E)w2 x | (9) |
Czas styku punktów na czynnej powierzchni elementów tocznych jest krótki. Można więc przyjąć, że wokół pola ich styku zachodzą adiabatyczne procesy cieplne i dla takiego przypadku można przyjąć, że przyrost temperatury wywołany zmianą stanu odkształcenia w jednej bieżni wynosi q = -hT k e, gdzie: hT = gT To /(ce k), k = lo /ce , gT = (3l+2G)•at/3Kat, e = 3at q +skk/(3K), lo - przewodność cieplna, ce - ciepło właściwe przy stałej deformacji odniesione do jednostki objętości, at - współczynnik rozszerzalności liniowej oraz moduł ściśliwości K = E/[3(l - 2n)] jak i pozostałe stałe materiałowe wyznaczone przy stałej temperaturze początkowej To[°K]. Przyjmując według Hertza, że w polu styku suma naprężeń głównych skk = -2p, dla płaskiego stanu naprężeń, prowadzi to do zależności przyrostu temperatury od zmiany stanu naprężenia
|
q1 = 2 p/[ce /at To] + 9 KT at | | (10) |
Zakładając czyste toczenie dwóch kół walcowych można, pomijając siły masowe, napisać równanie ruchu punktu w polu ich styku w postaci
|
G(d2ux/dx2) + (G + l)(d2ux/dx2) = g (dq1/dx) + g üx | (11) |
gdzie: ux - przemieszczenie a üx - przyspieszenie styczne, co po uwzględnieniu, że dx = v dt i przekształceniu prowadzi do
|
üx = v2gT (dq1 /dx) / [( 2G + l) - n2g] | (12) |
Wstawiając do tego równania zależności na q1 oraz na eliptyczny rozkład nacisku p = po[1-(x/b)2]-0,5
|
üx = v2 gT B po [(b/x)2-1] -0,5 / [(2G + l) - n2g] | (13) |
gdzie: B = 2/[(ce / atTo) + 9KTat].
Zmiana stanu naprężenia nie powoduje istotniejszych różnic temperatury w styku elementów tocznych, ale skokowe zmiany nacisku na jego granicach (x = ± b), a gdy v2 ® (2GT + lT )/g , to üx ® Ą co w całym polu ich styku, wywołują duże wartości przyspieszenia, które w sumie z przyspieszeniami Coriolisa mogą nie tyle wpływać na parametry sprzężenia ciernego, ile na naprężenia w bieżniach elementów tocznych, powodując przyspieszanie ich zużycia zmęczeniowego. Należy też zauważyć, że prędkość obwodowa, przy której v2 = (2GT + lT )/g równa się prędkości rozchodzenia się fali dylatacyjnej oznaczanej zazwyczaj jako c1.
Większe wartości wzrostu temperatury niż zmiana stanu odkształcenia, w polu styku elementów tocznych, wywołuje tarcie wewnętrzne, zwłaszcza w bieżniach wykonanych z materiałów lepko sprężystych, w których dyssypacja energii jest proporcjonalna do lepkości hk , która zależy od właściwości materiału bieżni oraz od częstotliwości zmian obciążenia. Przyjmując model Kelwina-Voigta można napisać, że ilość energii rozproszonej odniesiona do objętości w jednej bieżni równa się DE = 2hk ň éij • éijdt . Dewiator stanu odkształcenia określają zależności eij = eij - edij/3, 2eij = uij + uji, gdzie i oraz j = x, y lub z, co prowadzi w tym przypadku do wzrostu temperatury o wartość
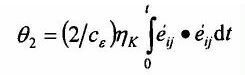 | (l4) |
gdzie prędkość zmiany dylatacji
|
éij = v{(ui,ix + uj,ix)/2 - atq,x + 2(l+v)vp[(b/x)2-1]-0,5/(9KT)dij} | (15) |
zaś ¶ uz/¶ x = x/rz, ¶ uz/¶ y = -x(drz/dy)/rz2, a promień zastępczy rz = r1r2/(r1 ± r2).
Największy przyrost temperatury w polu styku elementów tocznych wywołuje tarcie zewnętrzne powodowane poślizgiem vs. Wychodząc z równia Fouriera ¶ q/¶ t = (l0/ce )¶2q /¶ z2 wyprowadzono zależność na ten przyrost, która po przekształceniu przybiera postać q = 2µ p vs t0,5/(p l0 ce )0,5. Po uwzględnieniu eliptycznego rozkładu nacisku i wprowadzeniu prędkości toczenia v daje to
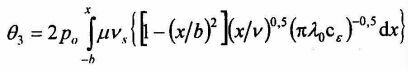 | (l6) |
W zależności (16) stałe materiałowe zależne są od temperatury, której sumaryczna wartość w miejscu styku elementów tocznych wynosi
gdzie: q(x,y) = q1 + q2 + q3 .
Temperatura ta określa warunki tarcia w sprzężeniu elementów tocznych. Jest ona przyczyną ich zacierania się. Zwiększa ono wielokrotnie współczynnik tarcia, a przez to może mieć bardzo istotny wpływ na parametry sprzężenia tych elementów.
Przedstawiony mechanizm sprzężenia w tarciu tocznym został rozszerzony o wpływ odkształceń promieniowych [2] oraz zweryfikowany doświadczalnie [3] w ramach realizacji grantu, w którym głównym wykonawcą był prof. Zbigniew Lawrowski.
|
| |
LITERATURA
- [l]
- KOZIARSK1 C., Sprzężenie koi ciernych przekładni bezstopniowych. Przegląd Mechaniczny 54 (1995).nr 4,s. l 1-18.
- [2]
- KOZIARSK1 C., Ein Modeli des Kupplungsmechanismus bei Waelzkoerpern. Tribologie und Schmierungstechnik 1998, Jg 45 H. 2, s. 37-45, 9 rys. bibliogr. 53 poz.
- [3]
- KOZIARSK1 C., LAWROWSKI Z., Experimentelle Untersuchung des Kupplungsmechanismim bei Walzreibung Tribologie und Schmierungstechnik 2000. Jg47 H. l, s. 34-39, 12 rys. bibliogr. 12 poz.
- [4]
- LUTZ O., Grundsatzliches tber stufenloss verstellbare Walzgetriebe. Konstruktion 7, (1955). H. 19. s. 330, Konstruktion 9 (1957) H. 5, s. 169. Konstruktion 10 (1958), H. 11, s. 425.
- [5]
- SKALSKI K., Zagadnienie kontaktowe dla ciała sprężysto-plastycznego. Warszawa WNT, 1986.
MODEL OF THE COUPLING IN ROLLING FRICTION
A new model of the rolling elements coupling mechanism is being presented in the paper. Apart from the geometrical, elastic and plastic deformation related slips in the area of the actuał contact of the two bodies, the mechanism includes also the slip generated by the temperature difference in the contact area. Other factors taken into account are the inertia forces related not only to the above mentioned tangential deformations but also to the radial deformations. These deformations are causing the additional centrifugal and circumferential (Coriolis) accelerations.
|