NEW APPROACH TO ACCOUNT FOR INDEPENDENT TRIBOLOGICAL TEST RESULTS THAT CANNOT BE CORRELATED IN A SIMPLE WAY
Andrzej Kulczycki
Central Petroleum Laboratory, Warsaw
* Corresponding author ak6 @ cln.pl
Czeslaw Kajdas
Central Petroleum Laboratory, Warsaw
In press: Tribology science and application
Summary
Introduction
General approach to tribochemical and research objective of the paper
Main assumptions of the model [1, 2]:
- As mentioned above, the model is supported by the methodology of tribochemical investigations. It means that we know everything about the system input (chemical structure and concentration of additives and physical properties of lubricants), we know conditions of friction process and finally we know the system output (results of the friction process, i.e., wear, type and concentration of stable products on metal surface and etc.);
- Usually, in tribochemical investigations we ask questions concerning lubricants ability to create the a boundary layer. The same question should be asked in the model.
- In the most of tribological investigations a result of the chosen tribotest is taken into account as a measure of the lubricant ability to create boundary layer. In the present authors perspective it is not good method to use test results directly as the measure of lubricants ability to create boundary layer. The test results are strongly controlled by an applied tribotester—type, properties of the friction elements, surface properties, and finally by test conditions. Consequently, conclusions on the different lubricant influence on boundary layer durability has to be related to the given test; thus, it is impossible to formulate general relationships.
- The question is: why there is no correlation between results of different tests. The answer to the question is simple: the boundary layer formation process is very complex one and, additionally, the mechanism of this process is
different in every test. The same lubricant can form boundary layer in relation to different mechanisms, but there is various activity of given lubricant in relation to different mechanisms. Moreover, different lubricants can form boundary layer in the same test corresponding to different mechanisms. Therefore, the general mechanism of boundary lubrication is still not well understood. The reason is explained below.
- In the time of test 1 lubricant creates boundary layer. The boundary layer formation process is very complex because it includes two basic processes A (AW—type of boundary layer) and B (EP—type of the layer). In the course of test 2 the same basic processes A and B are controlling the boundary layer formation process, however, the participation of each of the basic processes is different. Generally, it is possible to state that the ability of different lubricants/additives to AW and EP layer formation is different. This seems to be due ai the fact that there is no correlation between results of various tests.
- The main assumption of the presented method is that it is possible to differentiate/calculate participation of both AW and EP types of boundary layer portions generated under conditions of any tribological test.
- Test result y depends on the mechanism of boundary layer formation by a given lubricant. It will be very useful to find out function f(y), describing relationship between a test result and other parameters of the test. This function is related to the mechanism of boundary layer formation. Taking into account that there are many parameters connected with tribological processe during test, it is possible to find out more than one function concerning the mechanism of boundary layer formation. For example, one function is related to mechanical description of tribological process, the second function is related to chemical reaction description. It was assumed that the relationship between those functions enables analysis of the mechanism of tribological process on the "basic level". It means that conclusions should be more general and they are not strongly connected with the test procedure.
- Two functions were taking into account: f(y) and (f(y)). It was assumed, that in both these functions y was the only one variable.
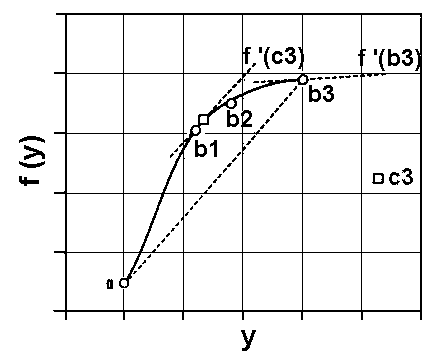
Fig 1. Dependence between f(y) end y for three tested lubricants. - b1 — test result for lubricant 1
- b2 — test result for lubricant 2
- b3 — test result for lubricant 3
- The analysis of two functions can be done by the use of Cauchy theorem.
[f(b) —f(a)]
[f(b) —f(a)]= [f '(b) —f '(a)]
[f '(b) —f '(a)](1) - Assuming, that a = const., it is interesting how y value changes when properties of tested lubricant change.
- Dependence (1) describes the relationship for every lubricant by three points: a, b and c. It will be difficult to use them using experimental data. It will be easier to use f ' (b) instead of f ' (c).
f ' (c) = b1 f ' (b) (2) and consequantly
f'(c) = b2 f'(b) (3) The dependence (1) is:
[f(b) —f(a)]
[f(b) —f(a)]= b1
b2f '(b)
f'(b)(4) b1
b2= ai ai = [f(b) —f(a)]
[f(b) —f(a)]: f '(b)
f'(b)(5) - Each of functions f(y) and f(y) are related to a tribological process which takes place during the given test. The relationship between functions f(y) and f(y) (5) makes it possible to relate test result to the mechanism of this tribological process. The same mechanism can be considered during different tests. It is to note that ai is non dimensional parameter value that corresponds with lubricant properties related to a given mechanism of tribological process. Accordingly, it can be assumed, that lubricants ability to create boundary layer may be expressed by this coefficient ai.
- Equation (5) is difficult to use in tribological applications. Functions f (y) and f(y) should be defined and described using parameters measured during test.
- One possibility is to describe tribological process using thermodynamic relationships. Then f (y) can be the work done on tribological system during test L, and f(y) can be dissipated energy ER. Then equation (5) can be written as follows:
ai = L — Lo
ER — ERox d ER
d ERo(6) where: L = µ P v t; where µ — friction coefficient; v — speed; t — time; P — is the applied test load
but it is difficult to define relationship ER = f(P); ER cannot be linear dependence of P. On the other hand, equation [6] can be expressed as:
ai = (L — Lo) • A = L•A — Lo•A (7) where: A = (d ER/d L)/(ER — E Ro) (8) 
Y = Y { tribological tests results } - The same relationship as (7) can be obtained using the vector description of tribological process is used. The ai coefficient can be related to the input expressed by vector X and the output expressed by vector Y in case the tribological process is described by the use of the vector model ai coefficient is scalar, so the relation between this coefficient and vector X or Y should be the scalar product of the input or output vector and another vector A:
ai = Ax • X (9) ai = Ay • Y (10) - The coordinates of vector X may be: concentration of additives, viscosity of lubricating oil or even results of another test carried out with the tested lubricant. The coordinates of vector Y may be
- results of the tribological test (wear),
- coefficient of friction,
- temperature generated during friction,
- concentration of durable/stable products on the friction solid surface, etc.
- Vectors Ax and Ay describe the relationship between lubricants ability to create boundary layer and the results of the tribological process. Consequently coordinates of these vectors can be divided into two groups: coordinates connected with a given tribological system and coordinates related to the tested lubricant (additive). Using affine coordinates, the scalar product of vectors Ax•X can be presented as ∑Ax nxn; for scalar products of vectors Ay•Y as ∑Ay nyn; accordingly ai= ∑ayy.
- Usually, in the tribochemical research we use one tester and one procedure of lubricant testing. The variable in the test can concern chemical structure and concentration of the additive. So coordinates of vector A , connected with tribological system should be constant for a given test procedure. Coordinates connected with tested lubricants may be different for various tested lubricants, but for the same group of lubricants/ additives they can be constant. What does it mean? The influence of all additives belonging to this group on creation of boundary layer is only quantitative but not qualitative. Thus, each additive creates boundary layer of different durability, but mechanism of the boundary layer formation is the same for all these additives.
- It was found, that this vector A should be constant when the same relation exists between
- the results of a given tribological process obtained for the chosen group of lubricants and
- the ability to create the boundary film of each lubricant, belonging to this group.
- Consequently it can be said, that vector A is constant in the case when the lubrication mechanism is the same for the considered group of lubricants and the same machine, working under the same conditions. As mentioned above, it has been assumed, that the mechanism of lubrication means the participation of two kinds of the boundary layer: antiwear type (AW) and extremme pressure type (EP). Taking into account suggestions concerning antiwear properties of lubricants presented by different researches like Dorison [3], Georges [4] and P;aza [5] it was admitted that AW type of the boundary layer exists between hydrodynamic/EHD films and EP type of the boundary layer. The EP film is produced by only chemical reactions of the lubricant additives with the friction surface.
- In that context, the mechanism of boundary lubrication holds two different types of the boundary protective film smarting from (i) pure AW up to (ii) pure EP layer. In this case equations (9) and (10) relate to the results of tribological process, depending only on the type of generated formed boundary layer, describe the AW property by aAW coefficient, and EP property by aEP coefficient. Consequently it was concluded, that every mechanism of boundary lubrication can be described by ai coefficient, when it is denned as the sum of aAW and aEP coefficients:
ai = a aAW + (1 — a) aEP (11) - Eqn. (11) can be used to calculate ai values if adequate experimental method to determine values of aAW and aEP coefficients is applied. Therefore, it is necessary to find out tribological experimental methods able to provide test results concerning lubricant's ability to create both AW and EP types of the boundary layer. In earlier work [1, 2] there were selected two different tests carried out using a four ball machine. The first test was used to determine seizure load Pt under the following operating conditions:
- rotating speed of upper ball 470 ±20 rpm,
- continuous load increase from 0 to the seizure load (Pt),
- seizure load detected by the measured friction coefficient.
- It was found that Pt value depends on durability of antiwear layer and aAW depends on Pt values according to eqn. (12)
aAW = (0,000086 n40 — 0,01) • 0,5 µ Pt² vs vp—1 +0,2 — 0,00073 n40 (12) where: n40 — kinematic viscosity of tested oil at 40 °C; vs — sliding velocity (0,18 m/s); vp — speed of load increase (45 N/s); µ — friction coefficient - The second test was used to determine welding load Pt at the following test conditions:
- rotating speed of upper ball 1470 ±30 rpm,
- stepwise load increase according to PN—76/C—04147,
- test duration of each step 10 s.
- It was found that Pw values depend on durability of EP type of the boundary layer and aEP coefficient can be calculated from eqn. (13)
aEP = 0,48 — 0,00013 PW (13) - Kajdas et al. [6] found a relationship between lubricants ability to EP boundary layer formation and reactivity of additives. The additives reactivity was determined by the use of hot wire method. The reactivity index RI was calculated on the basis of—changes of the wire electrical resistance. The present authors related this reactivity index to chemical structure of these additives. Fig. 2 demonstrates the obtained linear relationship between aEP and the reactivity index (RI).
- Previous research carried on in Central Laboratory of Petroleum [1] anabled to develop the following dependence for four ball and FZG machines test results:
az = u z + w (14) 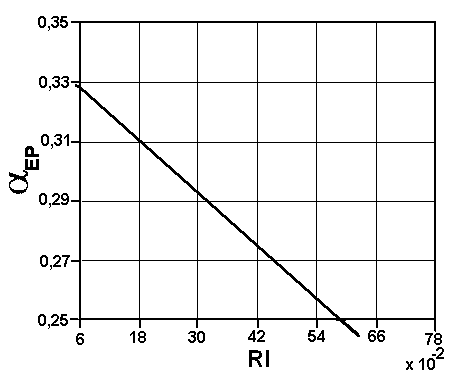
Fig. 2. Relationship between lubriconts ability to EP loyer formation, expressed by aEP coefficient and reactivity index Rl of ferrocene type additives of different detailed chemical structures. az is not the same as aAW; aAW is related to pure boundary layer created by molecules adsorbed or chemisorbed on metal surface. It occurs that wear process determined on the four ball machine depends not only on this type of boundary layer durability, but also on the EP type:
aFZG = w — u SFZG (15) where z is wear of balls, SFZG is the step of seizure load, u and w are empirically determined parameters that have constant values for the given type of lubricant and the given test—type. - This model was applied for tribochemical investigations and it occured that the model is very useful to explain some of tests results, especially on four ball and FZG machines.
Aplication of ai model in tribochemical investigations
The influence of base oil properties on the efficiency of action of ZDDP—type additives
- The aim of the work was focused on base oil interaction with ZDDP—type additives. The lubricants were formulated using the following base oils: SAE 5W, SAE 10W/95, SAE 30/85 and brighstock 30/85. Sixteen lubricant samples were prepared. Four different ZDDP additives were added to each of base oil. The concentration of Zn in each oil was 0,11 %. The following four ball test results were generated:
- weld load Pw,
- seizure load Pt,
- wear scar diameter d40.
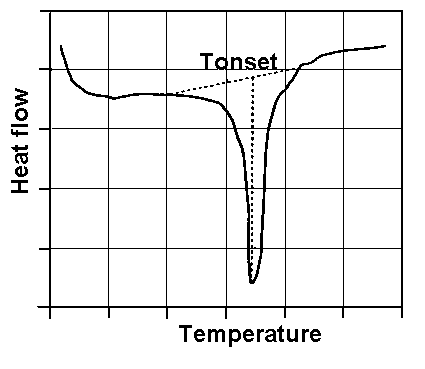
Fig. 3. Example of Tonset determination. - Each of pure additive was tested using DSC calorimeter. The value of Tonset temperature was measured.
- Tonset was selected as the measure of the tested ZDDP additives thermal stability. Pw and Pt test results were related to Tonset. It was found that the influence of ZDDP thermal stability on Pw (EP properties) depends on base oil viscosity. The same conclusion was drawn for Pt (AW properties). These findings are illustrated in Figs. 4 and 5, respectively.
- Using ai model the relationship between thermal stability of ZDDP, base oil viscosity and AW and EP properties of lubricants containing ZDDP was analysed. It was concluded that kinetic of ZDDP chemical changes during tribological process depends on base oil viscosity. Moreover, it was found that
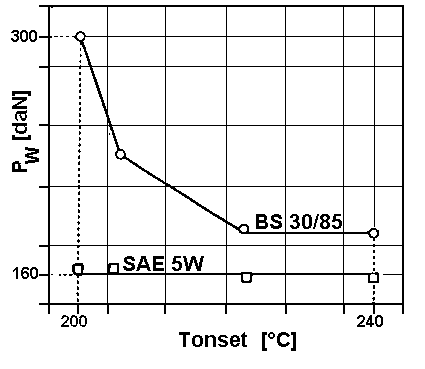
Fig. 4. Dependence between weld lood (Pw) ond ZDDP thetmol stability (Tonset). 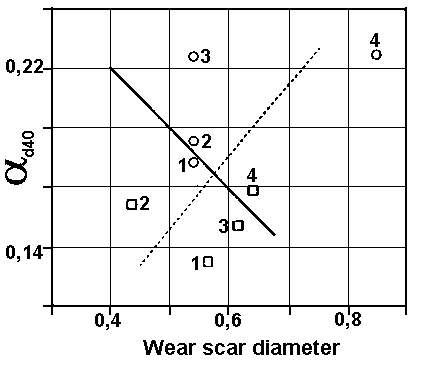
Fig. 5. Dependence between ad40 and wear scar diameter 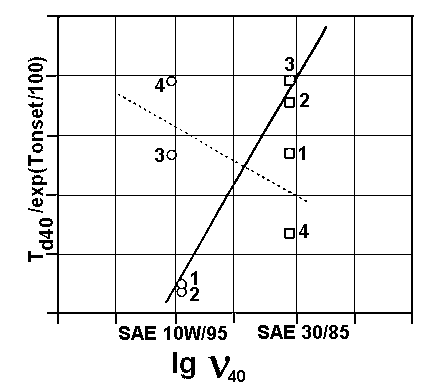
Fig. 6. Dependence between thermal stability of lubricant containing ZDDP and oil viscosity. the interaction between ZDDP and base oil takes place in the bulk lubricant, but not on the metal surface. This conclusion results from the additional DSC analysis of thermal stability of lubricants conaining ZDDP, as presented in Fig. 6. Detailed test results and analysis using ai model were described in [7]
Influence of surface coarsenes on tribochemistry of AW/EP layers produced by gear oils
- In the present paper usefulness of the model will be shown for determination of relation between friction surface coarseness, durability of boundary layer and chemical reactions in lubricating oils under test conditions. It is well known that initial coarseness of friction surface play important role in the boundary layer formation process. Additionally, the surface coarseness changes under friction conditions and the final coarseness depend on lubricant's properties, however, it is difficult to explain which oil property plays the major role. Authors of this paper tried to explain it using the following tribological tests:
- four ball machine wear test — 1 hour duration, loads in the range from 10 to 80 kG to determine wear values by measuring wears scar diameters; after completion of the test IR spectrum was obtained;
- standard FZG test; the coarseness of small tested wheel was prepared to obtain different Ra parameters; the step of seizure load was determined and the final coarseness was measured.
- Two gear oils: GL 3 and GL 4 (API class) SAE 80 W— 90 were prepared. GL 3 oil was formulated using ZDTP type additive; to produce GL 4 oil, full EP package of SP type additives was used. The test results of these gear oils are summarized in Tables 1 and 2.
Table 1.
Results of the four ball wear test (P — load; z — wear; p695—1350 x 10 —2 and p1500—1850 x 10 —2 — dotes calculated on the basis of IR spectra of used oils).lp P [daN ] Oil Z [mm ] az az p650—1350 x 10 —2 p1500—1850 x 10 —2 1 2 3 4 5 6 7 8 1 20 GL3 0,20 0,090 0,76 1,7 3,0 2 20 GL3 0,30 0,102 0,69 1,4 1,0 3 30 GL3 0,38 0,114 0,62 1,3 0,6 4 40 GL3 0,40 0,126 0,55 1,2 0,2 5 60 GL3 0,60 0,174 0,27 —0,5 —0,2 6 80 GL3 0,70 0,198 0,13 —1,0 —1,0 7 10 GL4 0,20 0,136 1,00 1,0 1,0 8 20 GL4 0,30 0,125 0,80 0,4 0,4 9 30 GL4 0,35 0,120 0,71 0,4 0,4 10 40 GL4 0,40 0,114 0,60 0,0 0,0 11 60 GL4 0,80 0,105 0,45 0,0 0,0 12 80 GL4 0,82 0,104 0,43 —0,4 —0,5 - Detailed analysis of the IR spectra led to the conclusion that it is not possible to use them to clearly account for proceeding chemical reactions of additives and base oil components during the wear test. On the other hand,
using QantIR program to interpret the obtained spectra it was possible to determine the effect of chemical reactions.Table 2.
Results of the FZG test.lp Oil SFZG aFZG aFZG Ra D Ra 1 2 3 4 5 6 7 1 GL3 8 0,15 0,40 0,020 —0,003 2 GL3 >12 0,10 0,80 0,135 0,076 3 GL3 11 0,12 0,60 0,240 0,068 4 GL3 10 0,13 0,50 0,500 0,156 5 GL3 10 0,13 0,50 0,990 0,405 6 GL4 10 0,13 0,80 0,020 —0,003 7 GL4 12 0,11 0,60 0,135 0,011 8 GL4 12 0,11 0,60 0,240 0,098 9 GL4 >12 0,10 0,40 0,500 0,163 10 GL4 >12 0,10 0,40 0,990 0,462 - The p695—1350 and p1500—1850 the quantitative measures of the chemical reactions effect of both the additives and base oil. The calculated values of p695—1350 and p1500—1850 are collected in Table 1.
- The results of tribological tests were adopted to ai model. First of all, for GL 3 and GL 4 oils the values of aAW and aEP were calculated on the basis of the four ball test results: Pt, Pw.
- The obtained values were as follows:
- for GL 3 oil: aAW = 0,050 and aEP = 0,22
- for GL 4 oil: aAW = 0,136 and aEP = 0,08
- Then the ability of tested oils to act as antiwear agents (az) was calculated using relationships developed during earlier investigations. These relationships are as follows [1]:
- for GL 3 oil: az = 0,24 z + 0,03
(16) - for GL 4 oil: aAW = 0,11 z (in the range of 10 — 40 daNa)
(17) - These relationships were found on the basis of measurements of mechanical factors only. General equation describing relation between oils ability to protect balls against wear and different outputs measured after the test is as follows:
az = az z + ap695—1350 p695—1350 + ap1500—1850p1500—1850 (18) - In case of GL3 oil
az = 0,24;
ap695—1350 p695—1350 + ap1500—1850p1500—1850 = 0,03(19) - In case of GL4 oil [in the range of 10 — 40 daN]
az = 0,11;
ap695—1350 p695—1350 + ap1500—1850p1500—1850 = 0,00(20) - The IR data from Table I were introduced to these equations. As the result of the equation system solution, the following values were calculated.
- For GL3 oil:
ap695—1350 = 2,58; ap1500—1850 = —0,46 (21) using these data the sum of
ap695—1350 p695—1350 + ap1500—1850p1500—1850 (22) was calculated for other test results:
- Table 1, Lp. 2: 2,58 x 0,014 — 0,46 x 0,010 = 0,0315
(23) - Table I, Lp. 4: 2,58 x 0,013 — 0,46 x 0,006 = 0,0307
(24) - For GL4 oil:
ap695—1350 = — ap1500—1850 (25) - Table 1, Lp. 7: ap695—1350 x 0,01 — ap695—1350 x 0,01 = 0,00
(26) - Table 1, Lp. 8: ap695—1350 x 0,004 — ap695—1350 x 0,004 = 0,00
(27) - The obtained calculated results demonstrate that values of parameters of equations formulated on the basis of ai model, using mechanical factors only, are in line with the results of tribochemical measurements. In this way it is possible to connect quantitatively the results of tribochemical investigations with mechanical effects of the boundary lubrication process.
- In the case of GL3 and GL4 oils the observed results of tribochemical reactions included changes of SP additives (695—1350 cm—1) and oxidation of hydrocarbons (1500—1850 cm—1). These reactions play important role in the boundary layer formation process under the four ball antiwear test conditions. The intensity of the SP type additive reaction was ten time less for GL4 oil than for GL3 oil. Dependence between applied load and participation of EP layer is similar for both tested oils. Accordingly, ZDTP additive in GL3 oil is more active in the antiwear layer formation process than SP package (containing high sulphur component) and the antiwear layer produced by ZDTP is also more durable.
- Similar equation was found for determination of both GL 3 and GL 4 oils ability to protect the gear of FZG machine against seizure (aFZG)
aFZG = 0,23 — 0,01 SFZG (28) - Now, taking into account that oils ability to generate the boundary layer relates to the sum of its ability to produce AW layer and EP layer, the participation of the AW layer in the process can be calculated from equation (20):
az = az aAW + (1 — az) aEP (29) and aFZG = aFZG aAW + (1 — aFZG) aEP (30) - Consequently:
- for GL 3 oil:
az = 0,24 z +0,03
aAW — aEP— aEP
aAW — aEP(31) - or GL 4 oil:
az = 0,11 z
aAW — aEP— aEP
aAW — aEP(32) - or both GL3 and GL 4 oil:
az = 0,23 — 0,01 SFZG
aAW — aEP— aEP
aAW — aEP(33) for GL 3 aFZG = 0,24 z +0,03
aAW — aEP— 0,23 —0,01 SFZG
aAW — aEP+ az (34) for GL 4 aFZG = 0,11 z
aAW — aEP— 0,23 — SFZG
aAW — aEP+ az (35) - This equation describes the relationship between the results of antiwear four ball test and FZG test. There was found the relationship between aFZG and initial coarseness of wheel (Ra), presented in Figure 7 and its change under the test conditions DRa) — as demonstrated in Figure 8.
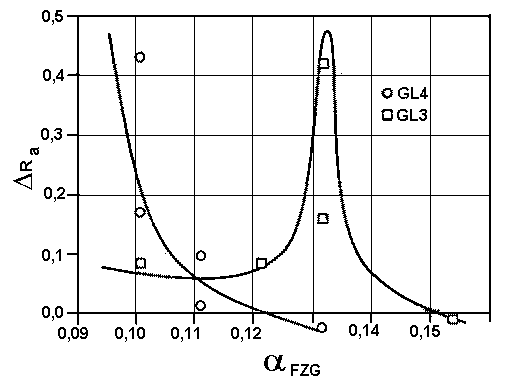
Fig. 7 Relationship between Ra and aFZG for GL3 and GL4 oils. - The above shown results allow to conclude that:
- For GL4 oil the participation of EP layer increases when initial coarseness increases; increase of surface coarseness is the reason that SP type additives can react with metal surface intensively and consequently durability of boundary layer increases;
- For GL3 oil when coarseness of surface increases the participation of EP layer increases as well, except for polished wheel where the participation of EP layer is great; for this oil the increase of EP layer participation leads to a decrease of the boundary layer durability.
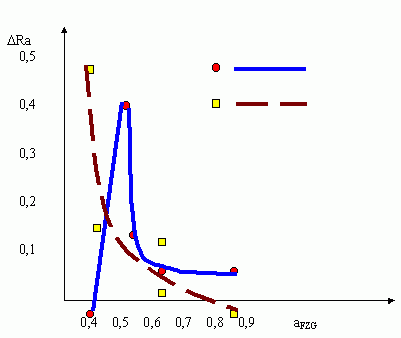
Fig. 8 Relationship between DRa and aFZG for GL3 and GL4 oils. - Using equations (34) and (35) it is possible to combine interpretation of the boundary layer formation in FZG test and adequate four ball wear test. These equations lead to aFZG = az and consequently aFZG = az. So it is possible to chose four ball apparatus test conditions (load) corresponding with az = FZGIntroducing appropriate data it is possible to combine aFZG activity of additives measured during the four ball machine testing. This equation was applied to compare the reactivity of ZDTP type additive in FZG test in the case when there was standard coarseness and when wheels were polished.
- For standard coarseness:
- aFZG = 0,8; aFZG = 0,10; az = 0,76 for load of 10 daN and az = 0,09
- for these conditions p695—1350 = 1,7 • 10—2; p1500—1850 = 3,0 • 10—2 and for polished wheel:
- aFZG = 0,4; aFZG = 0,15; az = 0,55 for load of 40 daN and az = 0,126
- for these conditions p695—1350 = 1,2 • 10 —2; p1500—1850 = 0,2 • 10 —2
- It points out that the reactivity of ZDTP additive in GL3 oil is smaller when the wheel is polished than in the case of the standard coarseness. It was —the major reason that the boundary layer durability was lower for the polished wheel.
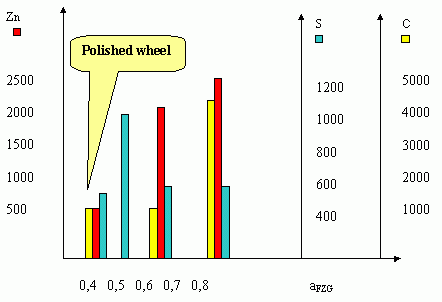
Fig. 11 Dependence of Zn, S and C concentration on aFZG value. - This conclusion was werified by the comparision of Zn, S and C concentration on wheels surface after FZG test for wheels of the sandard coarseness and for the polished one. The results are shown in Figure 9.
- These results are in agreement with the conclusion obtained as the effect of eqn. (34) analysis.
Conclusions
- Using ai model the relation between additives reactivity under friction conditions and durability of the generated boundary layer was determined.
- It was found that the mechanism of interaction between ZDDP &base oil depends on thermal stability of ZDDP & base oil properties, like viscosity.
- It was found that the coarseness of metal surface play very important role in forming the boundary layer structure.
- For SP type additives, containing mostly sulfur compounds, when the friction element coarseness increases, the participation of EP layer increases and the durability of the boundary layer increases as well.
- For ZDTP type additives, when coarseness of the wheel increases, the participation of EP layer increases, except for the polished wheel; here the main structure is EP. The increase of EP layer does not lead to increase of the boundary layer durability.
- Finaly, it can be concluded that ai model is useful in combining mechanical tribological test results with effects of measurements relating to tribochemical reactivity of additives.
Literature
- Kulczycki A. — Ocena działania dodatków smarnościowych w olejach przekładniowych; Wyd. Politechniki Poznanskiej, Rozprawy, Nr 324; Poznań
- Kulczycki A. — The correlation between results of different model friction tests in terms of energy analysis of friction and lubrication; Wear 103, 1985, p. 67—75.
- Dorison A., Ludema K.C. — Mechanics and chemistry in lubrication; Elsevier Sequoia Amsterdam.Oxford, New York, Tokyo 1985
- Georges J.M., Tonek A., Meille G., Belin M. — Chemical films and mixed lubrication; ASLE Trans. 26, 1983, p. 293—305.
- Płaza S. — Fizykochemia procesów tribologicznych; Wyd. Uniwersytetu Łódzkiego, Łódź 1997.
- Kajdas C., Dominiak M., Firkowski A., Dąbrowski J., Misterkiewicz B. — Chemical reactivity of a potential new group of EP additives of ferrocenyalalkyl sulfides; Mat 3rd International Tribology Congress Eurotrib 81, V.III, p. 121—135.
- Kulczycki A., Kajdas C.. —The Influence.of Base Oil Properties on the Efficiency of Action of ZDDP—type Additives; Lubrication Science 6—2 January 1994 p. 161—179.
- In the most of tribological investigations a result of the chosen tribotest is taken into account as a measure of the lubricant ability to create boundary layer. In the present authors perspective it is not good method to use test results directly as the measure of lubricants ability to create boundary layer. The test results are strongly controlled by an applied tribotester—type, properties of the friction elements, surface properties, and finally by test conditions. Consequently, conclusions on the different lubricant influence on boundary layer durability has to be related to the given test; thus, it is impossible to formulate general relationships.